Solução Final - Porto Seguro Data Challenge [3º lugar]
Confira a estratégia aplicada para a competição de machine learning do Porto Seguro hospedada no Kaggle

Introdução
Em Agosto e 2021 a Porto Seguro lançou um desafio no Kaggle que consistia em estimar a propensão de aquisição de novos produtos. Tratava-se de um problema de classificação e foi bem desafiador principalmente por 2 motivos:
- Todas as features da base de ddos eram anonimas;
- A métrica de avaliação foi a F1 Score (sensível à um ponto de corte)
Depois de 2 longos meses e dezenas de notebooks desenvolvidos, muitas submissões frustradas e muitas horas a menos de sono, cheguei em uma solução final que envole um blending de modelos e pseudo-labels e quando a competição acabou, percebi que uma solução mais simples de implementar teria um resultado privado ainda maior do que o notebook que selecionei. 😅
⚠️ Atenção!
Neste post abordarei uma solução mais simples e eficiente mas caso tenha interesse em conferir a solução final completa (um grande frankstein), já está publica la no github.
Este notebook é uma reescritura do meu notebook publicado no Kaggle em linguagem Python. Para quem acompanha meus posts de R pode achar meio estranho este notebook mas convido-o a tentar entender a solução pois foi desenvolvida pela perspectiva de um usuário nativo de R.
Espero que gostem! 🤘
Definição do problema de negócio
Segundo a descrição da competição:
Você provavelmente já recebeu uma ligação de telemarketing oferecendo um produto que você não precisa. Essa situação de estresse é minimizada quando você oferece um produto que o cliente realmente precisa.
Nessa competição você será desafiado a construir um modelo que prediz a probabilidade de aquisição de um produto.
Sobre a métrica de avaliação:
O critério utilizado para definição da melhor solução será o F1-Score, veja sua formula:
\[ F_1 = 2 \times \frac{precision \times recall}{precision + recall} \]
Note que tanto a Precision quanto a Recall precisam de um ponto de corte para obter as classes e por isso busquei otmizar as métricas ROC-AUC e Log Loss para obter estimativas de probabilidades com qualidade para finalmente calcular os pontos de corte que maximizam a F1.
Análise Exploratória (em R)
Antes de partir para modelagem fiz uma análise exploratória utilizando a linguagem R. Neste post tratarei de maneira bem breve e quem tiver interesse em conferir mais detalhes bem como os códigos dos gráficos basta acessar o notebook que deixei aberto no Kaggle.
Veja alguns gráficos:
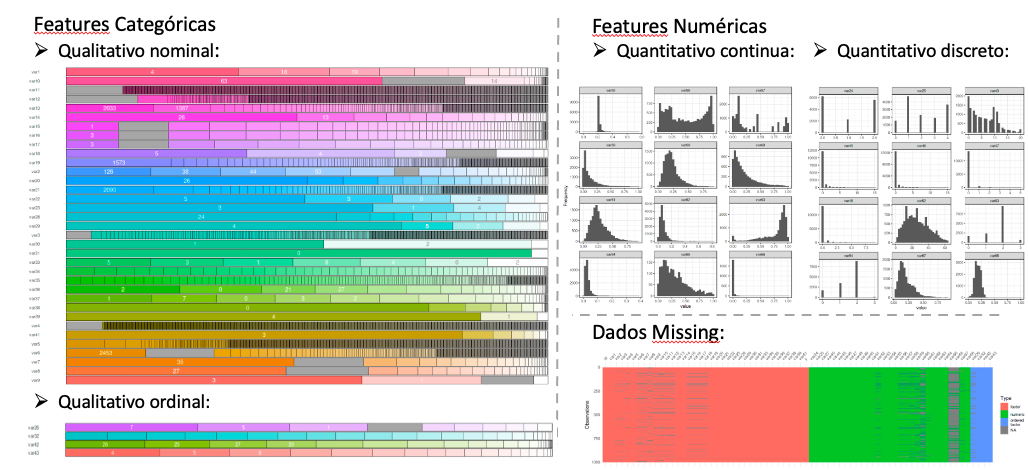
📌 Interpretação:
- Categóricas:
- Qualitativo nominal: Possuem muitas classes, poderia ser o nome do produto, região, um texto o que torna o desafio ainda maior para criar novas features;
- Qualitativo ordinal: Basicamente deixei como veio pois já tava como numerico;
- Numéricas:
- Quantitativo continua: Todas estão normalizadas (0, 1), algumas são bimodais, algumas assimétricas a direita (pode ser tempo ate alguma coisa);
-
Quantitativo discreto: Sem muito o que fazer, observação apenas a feature
var52que parece idade
- Dados missing: Parece haver algum padrão na maneira como os dados missing ocorrem e tentei substituir os
-999porNaN, imputar a média, a mediana e via outros modelos
Não achei que seria muito produtivo ficar adivinhando o que poderia ser cada feature pois praticamente todos as transformações e novas features que gerei não superavam o resultado do modelo ajustado nos dados da maneira que vinham portanto procurei investir mais tempo na modelagem mesmo.
Machine Learning (em Python)
Veja a estratégia de modelagem de maneira visual:

Importar dependências
Carregar pacotes do Python
# general packages
import pandas as pd
import numpy as np
import time
# knn features
from gokinjo import knn_kfold_extract
from gokinjo import knn_extract
# ml tools
from sklearn.model_selection import StratifiedKFold, KFold
from sklearn.metrics import f1_score, log_loss, roc_auc_score
# models
from catboost import CatBoostClassifier
from xgboost import XGBClassifier
# optimization
import optuna
# interpretable ml
import shap
# automl
from autogluon.tabular import TabularPredictor
# ignore specific warnings
import warnings
warnings.filterwarnings("ignore", message="ntree_limit is deprecated, use `iteration_range` or model slicing instead.")Definir funções auxiliares para calcular o ponto de corte que maximiza a F1:
def get_threshold(y_true, y_pred):
thresholds = np.arange(0.0, 1.0, 0.01)
f1_scores = []
for thresh in thresholds:
f1_scores.append(
f1_score(y_true, [1 if m>thresh else 0 for m in y_pred]))
f1s = np.array(f1_scores)
return thresholds[f1s.argmax()]
def custom_f1(y_true, y_pred):
max_f1_threshold = get_threshold(y_true, y_pred)
y_pred = np.where(y_pred>max_f1_threshold, 1, 0)
return f1_score(y_true, y_pred) Carregar dados da competição:
# load data
train = pd.read_csv('../input/porto-seguro-data-challenge/train.csv').drop('id', axis=1)
test = pd.read_csv('../input/porto-seguro-data-challenge/test.csv').drop('id', axis=1)
sample_submission = pd.read_csv('../input/porto-seguro-data-challenge/submission_sample.csv')
meta = pd.read_csv('../input/porto-seguro-data-challenge/metadata.csv')
# get data types
cat_nom = [x for x in meta.iloc[1:-1, :].loc[(meta.iloc[:,1]=="Qualitativo nominal")].iloc[:,0]]
cat_ord = [x for x in meta.iloc[1:-1, :].loc[(meta.iloc[:,1]=="Qualitativo ordinal")].iloc[:,0]]
num_dis = [x for x in meta.iloc[1:-1, :].loc[(meta.iloc[:,1]=="Quantitativo discreto")].iloc[:,0]]
num_con = [x for x in meta.iloc[1:-1, :].loc[(meta.iloc[:,1]=="Quantitativo continua")].iloc[:,0]] Stage 0: Feature Extraction com KNN
Esta técnica gera \(k \times c\) novas features, onde \(c\) é o número de classes da target. As novas features são calculadas a partir das distâncias entre as observações e seus k vizinhos mais próximos dentro de cada classe;
O valor para os \(K\) vizinhos mais próximos selecionado foi \(K=1\) e para isso utilizei a biblioteca
gokinjo que foi inspirada nas idéias apresentadas na solução vencedora do Otto Group Product Classification Challenge.
# convert to numpy because gokinjo expects np arrays
X = train[cat_nom+cat_ord+num_dis+num_con].to_numpy()
y = train.y.to_numpy()
X_test = test[cat_nom+cat_ord+num_dis+num_con].to_numpy()
# extract on train data
KNN_feat_train = knn_kfold_extract(X, y, k=1, normalize='standard')
print("KNN features for training set, shape: ", np.shape(KNN_feat_train))
# extract on test data
KNN_feat_test = knn_extract(X, y, X_test, k=1, normalize='standard')
print("KNN features for test set, shape: ", np.shape(KNN_feat_test))
# convert to dataframe
knn_feat_train = pd.DataFrame(KNN_feat_train, columns=["knn"+str(x) for x in range(knn_feat_train.shape[1])])
knn_feat_test = pd.DataFrame(KNN_feat_test, columns=["knn"+str(x) for x in range(knn_feat_test.shape[1])])## KNN features for training set, shape: (14123, 2)
## KNN features for test set, shape: (21183, 2)Stage 1: Tuning XGBoost com Optuna
Testei e otimizei muitos modelos como XGBoost, NGBoost, LightGBM, CatBoost, TabNet, HistGradientBoosting e algumas DNNs e em todos os casos (exceto DNNs) utilizei o Optuna para a seleção dos hiperparâmetros.
Também inclui nas tentativas iniciais de otimização alguns métodos de remostrarem como Random Under Sampling, Smote, Tomek, Adasyn dentre outros mas não tive muito sucesso.. apenas a combinação Tomek + CatBoost pareceu trazer algum ganho.
Claro que minhas tentativas não foram exautivas e devido ao tempo limitado acabei selecionando o XGBoost que foi o que apresentou as melhores métricas depois de otimizado e também o CatBoost com alguns hiperparâmetros fixos para serem a base deste pipeline.
Principais Informações 📌 :
- Nenhum pré-processamento;
- KFold K=10;
- Otimização de hiperparâmetros com Optuna;
- Loss do XGBoost: Log Loss;
- Loss do Otimizador: Log Loss;
- Sem resampling;
- Previsão final com a probabilidade média de 10 seeds diferentes
X_test = test[cat_nom+cat_ord+num_dis+num_con]
X = train[cat_nom+cat_ord+num_dis+num_con]
y = train.y
K=10
SEED=314
kf = KFold(n_splits=K, random_state=SEED, shuffle=True)fixed_params = {
'random_state': 9,
"objective": "binary:logistic",
"eval_metric": 'logloss',
'use_label_encoder':False,
'n_estimators':10000,
}
def objective(trial):
hyperparams = {
'clf':{
"booster": trial.suggest_categorical("booster", ["gbtree"]),
"lambda": trial.suggest_float("lambda", 1e-8, 5.0, log=True),
"alpha": trial.suggest_float("alpha", 1e-8, 5.0, log=True)
}
}
if hyperparams['clf']["booster"] == "gbtree" or hyperparams['clf']["booster"] == "dart":
hyperparams['clf']["max_depth"] = trial.suggest_int("max_depth", 1, 9)
hyperparams['clf']["eta"] = trial.suggest_float("eta", 0.01, 0.1, log=True)
hyperparams['clf']["gamma"] = trial.suggest_float("gamma", 1e-8, 1.0, log=True)
hyperparams['clf']["grow_policy"] = trial.suggest_categorical("grow_policy", ["depthwise", "lossguide"])
hyperparams['clf']['min_child_weight'] = trial.suggest_int('min_child_weight', 5, 20)
hyperparams['clf']["subsample"] = trial.suggest_float("subsample", 0.03, 1)
hyperparams['clf']["colsample_bytree"] = trial.suggest_float("colsample_bytree", 0.03, 1)
hyperparams['clf']['max_delta_step'] = trial.suggest_float('max_delta_step', 0, 10)
if hyperparams['clf']["booster"] == "dart":
hyperparams['clf']["sample_type"] = trial.suggest_categorical("sample_type", ["uniform", "weighted"])
hyperparams['clf']["normalize_type"] = trial.suggest_categorical("normalize_type", ["tree", "forest"])
hyperparams['clf']["rate_drop"] = trial.suggest_float("rate_drop", 1e-8, 1.0, log=True)
hyperparams['clf']["skip_drop"] = trial.suggest_float("skip_drop", 1e-8, 1.0, log=True)
params = dict(**fixed_params, **hyperparams['clf'])
xgb_oof = np.zeros(X.shape[0])
for fold, (train_idx, val_idx) in enumerate(kf.split(X=X, y=y)):
X_train = X.iloc[train_idx]
y_train = y.iloc[train_idx]
X_val = X.iloc[val_idx]
y_val = y.iloc[val_idx]
model = XGBClassifier(**params)
model.fit(X_train, y_train,
eval_set=[(X_val, y_val)],
early_stopping_rounds=150,
verbose=False)
xgb_oof[val_idx] = model.predict_proba(X_val)[:,1]
del model
return log_loss(y, xgb_oof)Como no Kaggle existe o limite de aproximadamente 8h para executar um notebook, coloquei um limite de 7.5 horas para a busca de hiperparâmetros:
study_xgb = optuna.create_study(direction='minimize')
study_xgb.optimize(objective,
timeout=60*60*7.5,
gc_after_trial=True)Resultados da busca:
print('-> Number of finished trials: ', len(study_xgb.trials))
print('-> Best trial:')
trial = study_xgb.best_trial
print('\tValue: {}'.format(trial.value))
print('-> Params: ')
trial.params## -> Number of finished trials: 197
## -> Best trial:
## Value: 0.3028443879614926
## -> Params:
## {'booster': 'gbtree',
## 'lambda': 9.012384508756378e-07,
## 'alpha': 0.7472040331088792,
## 'max_depth': 5,
## 'eta': 0.01507605562231303,
## 'gamma': 1.0214961302342215e-08,
## 'grow_policy': 'lossguide',
## 'min_child_weight': 5,
## 'subsample': 0.9331005225916879,
## 'colsample_bytree': 0.25392142363325004,
## 'max_delta_step': 5.685109389498008}Acompanhar o histórico de cada etapa da otimização:
plot_optimization_history(study_xgb)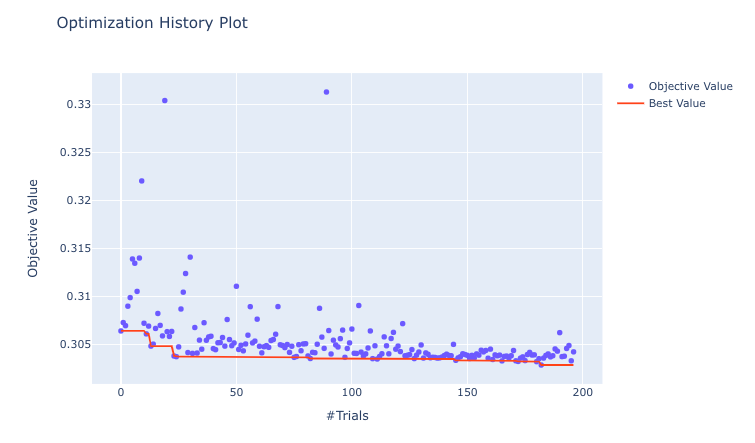
Avaliar as combinações de hiperparâmetros mais bem sucedidas:
optuna.visualization.plot_parallel_coordinate(study_xgb)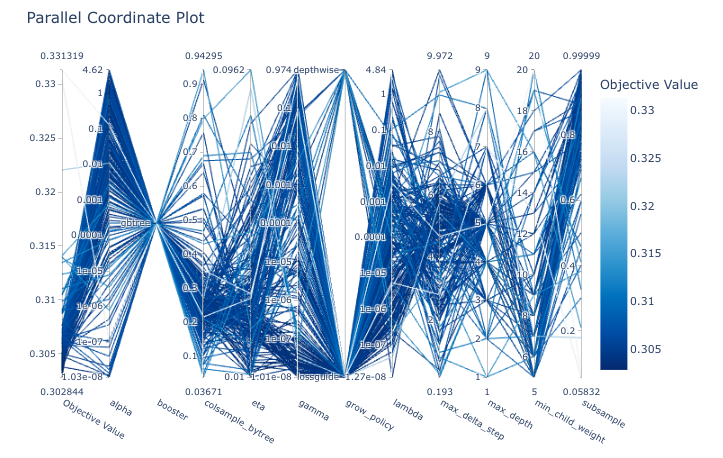
Quais hiperparâmetros tiveram mais impacto na modelagem:
plot_param_importances(study_xgb)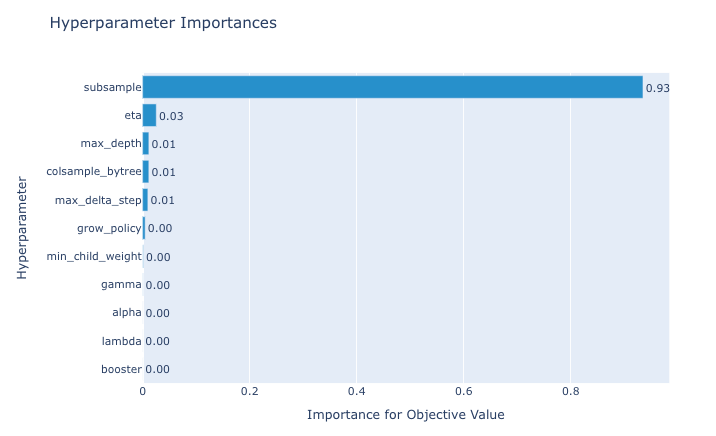
Após as 7.5 horas de busca, a melhor combinação encontrada para o XGBoost foi a seguinte:
# After 7.5 hours...
study_xgb = {'booster': 'gbtree',
'lambda': 9.012384508756378e-07,
'alpha': 0.7472040331088792,
'max_depth': 5,
'eta': 0.01507605562231303,
'gamma': 1.0214961302342215e-08,
'grow_policy': 'lossguide',
'min_child_weight': 5,
'subsample': 0.9331005225916879,
'colsample_bytree': 0.25392142363325004,
'max_delta_step': 5.685109389498008}Preparar lista de hiperparâmetros do XGBoost:
final_params_xgb = dict()
final_params_xgb['clf']=dict(**fixed_params, **study_xgb)Stage 2: Calcular Out-Of-Fold SHAP values
Após obter a melhor combinação de hiperparâmetros para o XGBoost e encontrar resultados formidáveis com o CatBoost modificando apenas alguns hiperparâmetros, resolvi tentar utilizar a informação adquirida pelo SHAP values desses modelos como entrada para novos modelos.
Algumas vantagens de se usar o shap values como um método de encoder dos dados, segundo este notebook publicado no Kaggle (muito interessante por sinal):
- Normaliza os dados;
- Mais ou menos Linearizado pois as features são transformadas em suas importâncias;
- Recursos categóricos codificados de maneira mais inteligente (A codificação não é linear e depende de outros recursos da amostra);
- Tratamento mais inteligente para valores missing.
Para evitar data leak, o SHAP values foi calculado em cima dos dados out-of-fold para os dados de treino e a média da previsão de todos os fold nos dados de teste.
Definir estratégia de validação cruzada:
X_test = test[cat_nom+cat_ord+num_dis+num_con]
X = train[cat_nom+cat_ord+num_dis+num_con]
y = train.y
K=15 # number of bins with Sturge’s rule
SEED=123
kf = StratifiedKFold(n_splits=K, random_state=SEED, shuffle=True)XGBoost
Obter out-of-fold SHAP do modelo XGBoost tunado:
shap1_oof = np.zeros((X.shape[0], X.shape[1]))
shap1_test = np.zeros((X_test.shape[0], X_test.shape[1]))
model_shap1_oof = np.zeros(X.shape[0])
for fold, (train_idx, val_idx) in enumerate(kf.split(X=X, y=y)):
print(f"➜ FOLD :{fold}")
X_train = X.iloc[train_idx]
y_train = y.iloc[train_idx]
X_val = X.iloc[val_idx]
y_val = y.iloc[val_idx]
start = time.time()
model = XGBClassifier(**final_params_xgb['clf'])
model.fit(X_train, y_train,
eval_set=[(X_val, y_val)],
early_stopping_rounds=150,
verbose=False)
model_shap1_oof[val_idx] += model.predict_proba(X_val)[:,1]
print("Final F1 :", custom_f1(y_val, model_shap1_oof[val_idx]))
print("Final AUC :", roc_auc_score(y_val, model_shap1_oof[val_idx]))
print("Final LogLoss:", log_loss(y_val, model_shap1_oof[val_idx]))
explainer = shap.TreeExplainer(model)
shap1_oof[val_idx] = explainer.shap_values(X_val)
shap1_test += explainer.shap_values(X_test) / K
print(f"elapsed: {time.time()-start:.2f} sec\n")
shap1_oof = pd.DataFrame(shap1_oof, columns = [x+"_shap1" for x in X.columns])
shap1_test = pd.DataFrame(shap1_test, columns = [x+"_shap1" for x in X_test.columns])
print("Final F1 :", custom_f1(y, model_shap1_oof))
print("Final AUC :", roc_auc_score(y, model_shap1_oof))
print("Final LogLoss:", log_loss(y, model_shap1_oof))## ➜ FOLD :0
## Final F1 : 0.7032967032967034
## Final AUC : 0.902330627099664
## Final LogLoss: 0.2953604946129216
## elapsed: 62.58 sec
##
## ➜ FOLD :1
## Final F1 : 0.6193853427895981
## Final AUC : 0.8613101903695408
## Final LogLoss: 0.34227429854659686
## elapsed: 45.96 sec
##
## ➜ FOLD :2
## Final F1 : 0.6793478260869567
## Final AUC : 0.8945898656215007
## Final LogLoss: 0.3085819148842589
## elapsed: 58.84 sec
##
## ➜ FOLD :3
## Final F1 : 0.7073791348600509
## Final AUC : 0.9058020716685331
## Final LogLoss: 0.2881665477053405
## elapsed: 62.24 sec
##
## ➜ FOLD :4
## Final F1 : 0.7239583333333334
## Final AUC : 0.9053121500559911
## Final LogLoss: 0.29320601468396107
## elapsed: 93.74 sec
##
## ➜ FOLD :5
## Final F1 : 0.7009803921568627
## Final AUC : 0.9076567749160134
## Final LogLoss: 0.2872539995859452
## elapsed: 73.34 sec
##
## ➜ FOLD :6
## Final F1 : 0.6736292428198434
## Final AUC : 0.8822788353863381
## Final LogLoss: 0.320014158050091
## elapsed: 55.16 sec
##
## ➜ FOLD :7
## Final F1 : 0.7135416666666666
## Final AUC : 0.9016657334826428
## Final LogLoss: 0.29617989833438774
## elapsed: 74.49 sec
##
## ➜ FOLD :8
## Final F1 : 0.7135135135135134
## Final AUC : 0.8893825776158104
## Final LogLoss: 0.29351621553572266
## elapsed: 93.71 sec
##
## ➜ FOLD :9
## Final F1 : 0.7391304347826086
## Final AUC : 0.9064054944284814
## Final LogLoss: 0.28033187155768635
## elapsed: 95.65 sec
##
## ➜ FOLD :10
## Final F1 : 0.684863523573201
## Final AUC : 0.9031046324199313
## Final LogLoss: 0.29823173886367804
## elapsed: 64.70 sec
##
## ➜ FOLD :11
## Final F1 : 0.704225352112676
## Final AUC : 0.8882052000840984
## Final LogLoss: 0.30525241732057884
## elapsed: 50.06 sec
##
## ➜ FOLD :12
## Final F1 : 0.6666666666666666
## Final AUC : 0.8905529469479291
## Final LogLoss: 0.313654842143217
## elapsed: 78.45 sec
##
## ➜ FOLD :13
## Final F1 : 0.6500000000000001
## Final AUC : 0.8745111780783517
## Final LogLoss: 0.3300786509821235
## elapsed: 59.54 sec
##
## ➜ FOLD :14
## Final F1 : 0.7135416666666666
## Final AUC : 0.9063284042329526
## Final LogLoss: 0.29314716930177404
## elapsed: 70.28 sec
##
## Final F1 : 0.6822461331540014
## Final AUC : 0.8945288307257988
## Final LogLoss: 0.30301717097927483CatBoost
Obter out-of-fold SHAP do modelo CatBoost + features extratídas via KNN:
X = pd.concat([X, knn_feat_train], axis=1)
X_test = pd.concat([X_test, knn_feat_test], axis=1)shap2_oof = np.zeros((X.shape[0], X.shape[1]))
shap2_test = np.zeros((X_test.shape[0], X_test.shape[1]))
model_shap2_oof = np.zeros(X.shape[0])
for fold, (train_idx, val_idx) in enumerate(kf.split(X=X, y=y)):
print(f"➜ FOLD :{fold}")
X_train = X.iloc[train_idx]
y_train = y.iloc[train_idx]
X_val = X.iloc[val_idx]
y_val = y.iloc[val_idx]
start = time.time()
model = CatBoostClassifier(random_seed=SEED,
verbose = 0,
n_estimators=10000,
loss_function= 'Logloss',
use_best_model=True,
eval_metric= 'Logloss')
model.fit(X_train, y_train,
eval_set = [(X_val,y_val)],
early_stopping_rounds = 100,
verbose = False)
model_shap2_oof[val_idx] += model.predict_proba(X_val)[:,1]
print("Final F1 :", custom_f1(y_val, model_shap2_oof[val_idx]))
print("Final AUC :", roc_auc_score(y_val, model_shap2_oof[val_idx]))
print("Final LogLoss:", log_loss(y_val, model_shap2_oof[val_idx]))
explainer = shap.TreeExplainer(model)
shap2_oof[val_idx] = explainer.shap_values(X_val)
shap2_test += explainer.shap_values(X_test) / K
print(f"elapsed: {time.time()-start:.2f} sec\n")
shap2_oof = pd.DataFrame(shap2_oof, columns = [x+"_shap" for x in X.columns])
shap2_test = pd.DataFrame(shap2_test, columns = [x+"_shap" for x in X_test.columns])
print("Final F1 :", custom_f1(y, model_shap2_oof))
print("Final AUC :", roc_auc_score(y, model_shap2_oof))
print("Final LogLoss:", log_loss(y, model_shap2_oof))## ➜ FOLD :0
## Final F1 : 0.6972010178117048
## Final AUC : 0.8954157334826428
## Final LogLoss: 0.29952314366911725
## elapsed: 22.84 sec
##
## ➜ FOLD :1
## Final F1 : 0.6348448687350835
## Final AUC : 0.8628429451287795
## Final LogLoss: 0.3407490151943705
## elapsed: 12.59 sec
##
## ➜ FOLD :2
## Final F1 : 0.6809651474530831
## Final AUC : 0.8949538073908175
## Final LogLoss: 0.3066089330852162
## elapsed: 18.03 sec
##
## ➜ FOLD :3
## Final F1 : 0.702247191011236
## Final AUC : 0.9107992721164613
## Final LogLoss: 0.2877216893570601
## elapsed: 15.66 sec
##
## ➜ FOLD :4
## Final F1 : 0.7131367292225201
## Final AUC : 0.9018687010078387
## Final LogLoss: 0.2976481761596595
## elapsed: 29.35 sec
##
## ➜ FOLD :5
## Final F1 : 0.7055837563451777
## Final AUC : 0.909231522956327
## Final LogLoss: 0.28834373773423566
## elapsed: 15.35 sec
##
## ➜ FOLD :6
## Final F1 : 0.6631578947368421
## Final AUC : 0.8796402575587906
## Final LogLoss: 0.32303153676573987
## elapsed: 19.13 sec
##
## ➜ FOLD :7
## Final F1 : 0.6997389033942559
## Final AUC : 0.901637737961926
## Final LogLoss: 0.2985978485411335
## elapsed: 23.30 sec
##
## ➜ FOLD :8
## Final F1 : 0.6965699208443271
## Final AUC : 0.8825565912117177
## Final LogLoss: 0.3009859242847037
## elapsed: 20.19 sec
##
## ➜ FOLD :9
## Final F1 : 0.7435897435897436
## Final AUC : 0.9042469689536757
## Final LogLoss: 0.28276851015512977
## elapsed: 24.39 sec
##
## ➜ FOLD :10
## Final F1 : 0.6767676767676767
## Final AUC : 0.902712173242694
## Final LogLoss: 0.29999812838692497
## elapsed: 16.14 sec
##
## ➜ FOLD :11
## Final F1 : 0.7013698630136986
## Final AUC : 0.8865022075828719
## Final LogLoss: 0.3081393413008847
## elapsed: 13.50 sec
##
## ➜ FOLD :12
## Final F1 : 0.6630434782608696
## Final AUC : 0.8920456934613498
## Final LogLoss: 0.31338640296724246
## elapsed: 24.48 sec
##
## ➜ FOLD :13
## Final F1 : 0.6485148514851485
## Final AUC : 0.8689887167986544
## Final LogLoss: 0.3369797070301582
## elapsed: 17.17 sec
##
## ➜ FOLD :14
## Final F1 : 0.7108753315649867
## Final AUC : 0.8994743850304856
## Final LogLoss: 0.301420230674656
## elapsed: 16.51 sec
##
## Final F1 : 0.6823234134098244
## Final AUC : 0.892656043550729
## Final LogLoss: 0.305726567456891train = pd.concat([train, shap1_oof], axis=1)
test = pd.concat([test, shap1_test], axis=1)
train = pd.concat([train, shap2_oof], axis=1)
test = pd.concat([test, shap2_test], axis=1)Stage 3: Modelo Final com AutoGluon
AutoGluon é um AutoML desenvolvido pela Amazon muito fácil de utilizar (no melhor estilo sklearn com métodos .fit() e .predict()).
Principais Informações 📌 :
- Inputs: Dataset original + knn features + Shapt values do XGBoost tunado e do CatBoost;
- Loss do XGBoost: Log Loss;
- Loss do CatBoost: AUC;
- Loss do AutoGluon: Log Loss;
- Tempo de processamento: 7h30m
💡 Insight
Um recurso muito útil do AutoGluon é poder acessar as previsões out-of-folds, o que facilita no cálculo do threshold que maximiza a F1 Score.
predictor = TabularPredictor(label="y",
problem_type='binary',
eval_metric="log_loss",
path='./AutoGlon/',
verbosity=1)
predictor.fit(train, presets='best_quality', time_limit=60*60*7.5)
results = predictor.fit_summary()## *** Summary of fit() ***
## Estimated performance of each model:
## model score_val pred_time_val fit_time pred_time_val_marginal fit_time_marginal stack_level can_infer fit_order
## 0 WeightedEnsemble_L2 -0.299310 30.410467 8888.826963 0.001654 2.456810 2 True 14
## 1 CatBoost_BAG_L1 -0.301038 3.051793 2376.887100 3.051793 2376.887100 1 True 7
## 2 WeightedEnsemble_L3 -0.301722 194.034947 22907.669139 0.001541 2.008858 3 True 26
## 3 LightGBMXT_BAG_L2 -0.302135 131.534432 17201.299530 1.378576 389.400378 2 True 15
## 4 LightGBMXT_BAG_L1 -0.302562 3.570399 969.385833 3.570399 969.385833 1 True 3
## 5 CatBoost_BAG_L2 -0.302646 131.912474 17619.939451 1.756617 808.040299 2 True 19
## 6 LightGBM_BAG_L2 -0.303002 131.422007 17281.518763 1.266150 469.619612 2 True 16
## 7 LightGBM_BAG_L1 -0.303264 2.964433 1038.037160 2.964433 1038.037160 1 True 4
## 8 XGBoost_BAG_L1 -0.303471 4.475003 2036.551052 4.475003 2036.551052 1 True 11
## 9 NeuralNetFastAI_BAG_L1 -0.304455 19.917584 3434.894841 19.917584 3434.894841 1 True 10
## 10 XGBoost_BAG_L2 -0.304499 132.757505 17834.135370 2.601648 1022.236218 2 True 23
## 11 NeuralNetFastAI_BAG_L2 -0.306339 142.018741 18777.287244 11.862885 1965.388093 2 True 22
## 12 LightGBMLarge_BAG_L2 -0.306606 131.701429 18260.504603 1.545573 1448.605452 2 True 25
## 13 NeuralNetMXNet_BAG_L2 -0.308237 177.769179 19273.211899 47.613322 2461.312748 2 True 24
## 14 LightGBMLarge_BAG_L1 -0.309686 3.042399 2629.185346 3.042399 2629.185346 1 True 13
## 15 ExtraTreesEntr_BAG_L2 -0.314045 132.017535 16815.886061 1.861679 3.986910 2 True 21
## 16 RandomForestEntr_BAG_L2 -0.314454 132.061970 16843.769642 1.906114 31.870490 2 True 18
## 17 ExtraTreesGini_BAG_L2 -0.314960 132.123651 16816.087081 1.967794 4.187930 2 True 20
## 18 NeuralNetMXNet_BAG_L1 -0.317156 81.677096 4258.886806 81.677096 4258.886806 1 True 12
## 19 RandomForestGini_BAG_L2 -0.321702 132.035970 16835.326491 1.880114 23.427339 2 True 17
## 20 ExtraTreesEntr_BAG_L1 -0.323283 1.794093 4.051307 1.794093 4.051307 1 True 9
## 21 RandomForestEntr_BAG_L1 -0.324296 1.966043 33.380685 1.966043 33.380685 1 True 6
## 22 ExtraTreesGini_BAG_L1 -0.325897 1.796291 3.748723 1.796291 3.748723 1 True 8
## 23 RandomForestGini_BAG_L1 -0.328218 1.778995 22.705248 1.778995 22.705248 1 True 5
## 24 KNeighborsDist_BAG_L1 -1.070156 2.010938 2.075571 2.010938 2.075571 1 True 2
## 25 KNeighborsUnif_BAG_L1 -1.071373 2.110790 2.109480 2.110790 2.109480 1 True 1
## Number of models trained: 26
## Types of models trained:
## {'StackerEnsembleModel_RF', 'StackerEnsembleModel_NNFastAiTabular', 'WeightedEnsembleModel', 'StackerEnsembleModel_XGBoost', 'StackerEnsembleModel_CatBoost', 'StackerEnsembleModel_KNN', 'StackerEnsembleModel_LGB', 'StackerEnsembleModel_XT', 'StackerEnsembleModel_TabularNeuralNet'}
## Bagging used: True (with 10 folds)
## Multi-layer stack-ensembling used: True (with 3 levels)
## Feature Metadata (Processed):
## (raw dtype, special dtypes):
## ('float', []) : 152 | ['var55', 'var56', 'var57', 'var58', 'var59', ...]
## ('int', []) : 48 | ['var1', 'var2', 'var3', 'var4', 'var5', ...]
## ('int', ['bool']) : 6 | ['var27', 'var31', 'var44', 'var49', 'var50', ...]
## Plot summary of models saved to file: ./AutoGlon/SummaryOfModels.html
## *** End of fit() summary ***Nota: Os resultados podem variar devido à natureza estocástica do algoritmo ou procedimento de avaliação.
# get final predictions
y_oof = predictor.get_oof_pred_proba().iloc[:,1]
y_pred = predictor.predict_proba(test).iloc[:,1]final_threshold = get_threshold(train.y, y_oof)
final_threshold## 0.31print("Final F1 :", custom_f1(y, y_oof))
print("Final AUC :", roc_auc_score(y, y_oof))
print("Final LogLoss:", log_loss(y, y_oof))## Final F1 : 0.6846193682030037
## Final AUC : 0.8961328807692966
## Final LogLoss: 0.2993098559321765Após submissão:
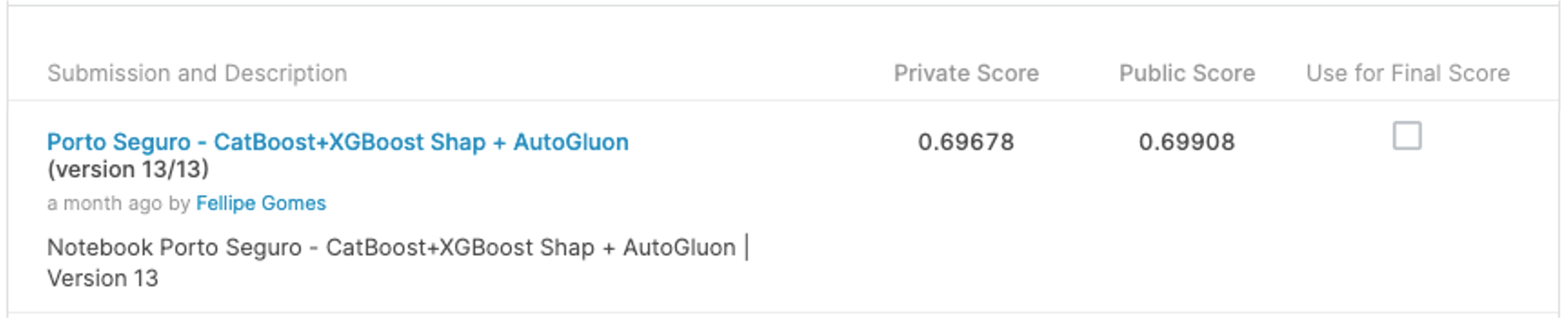
Conclusão
Gostaria de agradecer imensamente ao time do Porto Seguro pela iniciativa, pois esse tipo de competição (tão detalhada e desafiadora) não tem sido muito comum no Brasil e é muito importante para fomentar a comunidade brasileira de ciência de dados!
Sabemos que o “mundo real” é diferente do mundo das competições (onde buscamos o melhor score a todo custo) porém, na minha visão, não deixa de ser um ótimo exercício para treinar o raciocínio analítico.. além de ser muito empolgante e divertido!
Tive o enorme prazer de trocar idéias e conhecer pessoas fora da curva bem como me tornar fã de alguns competidores! A cada semana q passava o nível estava cada vez mais alto!
Com certeza este pipeline poderia ser muito melhor, sinto que poderia ter gasto mais tempo com feature engineering e tido mais paciencia com alguns modelos. Tentei fazer o melhor que pude com o tempo disponível e me sinto muito grato pela experiência de apresentar os resultados e aprender bastante com a solução dos top colocados.
Não acaba por aqui! Agora é hora de voltar aos estudos, continuar praticando com as TPS’s do Kaggle e, quem sabe, ir melhor na próxima!






























Share this post
Twitter
LinkedIn
Email