Análise Multivariada
Esse é o primeiro post do ano e como no ano de 2017 falou-se tanto das maravilhas computacionais desta onda do Big Data e em contra partida, identificamos que deste 2004 a popularidade pelo termo “estatística” vem diminuindo como mostrei em uma breve pesquisa neste post sobre a API do googletrends sinto que existe uma necessidade de se ampliar também a divulgação dos métodos estatísticos pois o aprofundamento na teoria é fundamental (é muito fácil achar resultados sem fundamento apenas “apertando botão”), como as ferramentas da estatística multivariada que muitas vezes servem como soluções para essas grandes quantidades de dados
Diversas vezes nos deparamos com bases de dados que envolvem além de muitas observações, muitas variáveis, especialmente nas análises de fenômenos ou processos sociais, psicológicos, educacionais e econômicos bem como na área da química, biologia, geologia, marketing, medicina, medicina veterinária, dentre muitas outras.
Com as ferramentas estatísticas da análise multivariada somos capazes de identificar muitos elementos que podem ter relevância na análise dos dados, dois exemplos de ferramentas importantes são as que permitem encontrar fatores que não são diretamente observáveis com base em um conjunto de variáveis observáveis e as que permitem agrupar conjuntos de dados que possuem características semelhantes com algorítimos computacionais (chamados de aprendizados não-supervisionados ou semi-supervisionados em machine learning) e a partir dai estudar as novas classificações.
Neste post será apresentado algumas soluções para o caso em que existe a necessidade de avaliar um grande conjunto de dados com muitas variáveis e não temos muitas informações a respeito.
Análise Fatorial
Na análise fatorial buscamos fatores que explicam parte da variância total dos dados, os fatores são as somas das variâncias originais.
Objetivo da análise fatorial:
Procura identificar fatores que não são diretamente observáveis, com base em um conjunto de variáveis observáveis.
Explicar a correlação ou covariância, entre um conjunto de variáveis, em termos de um número limitado de variáveis não-observáveis, chamadas de fatores ou variáveis latentes.
Em casos nos quais se tem um número grande de variáveis medidas e correlacionadas entre si, seria possível identificar-se um número menor de variáveis alternativas, não correlacionadas e que de algum modo sumarizassem as informações principais das variáveis originais.
A partir do momento em que os fatores são identificados, seus valores numéricos, chamados de escores, podem ser obtidos para cada elemento amostral. Conseqüentemente, estes escores podem ser utilizados em outras análises que envolvam outras técnicas estatísticas, como análise de regressão ou análise de variância, por exemplo.
Etapas para realização
Computação da matriz de correlações para as variáveis originais;
Extração de fatores
Rotação dos fatores para tonar a interpretação mais fácil;
Cálculo dos escores dos fatores
Matriz de Correlação:
- Teste de Bartlett - a hipótese nula da matriz de correlação ser uma matriz identidade ( \(| R | = 1\) ), isto é, avalia se os componentes fora da diagonal principal são zero. O resultado significativo indica que existem algumas relações entre as variáveis.
No R:
Bartlett.sphericity.test <- function(x)
{
method <- "Teste de esfericidade de Bartlett"
data.name <- deparse(substitute(x))
x <- subset(x, complete.cases(x)) # Omitindo valores faltantes
n <- nrow(x)
p <- ncol(x)
chisq <- (1-n+(2*p+5)/6)*log(det(cor(x)))
df <- p*(p-1)/2
p.value <- pchisq(chisq, df, lower.tail=FALSE)
names(chisq) <- "X-squared"
names(df) <- "df"
return(structure(list(statistic=chisq, parameter=df, p.value=p.value,
method=method, data.name=data.name), class="htest"))
}
Bartlett.sphericity.test(dados)##
## Teste de esfericidade de Bartlett
##
## data: dados
## X-squared = 2590.3, df = 55, p-value < 2.2e-16- Teste KMO (Kaiser-Meyer-Olkin) - avalia a adequação do tamanho amostra. Varia entre 0 e 1, onde: zero indica inadequado para análise fatorial, aceitável se for maior que 0.5, recomendado acima de 0.8.
No R:
kmo = function(x)
{
x = subset(x, complete.cases(x))
r = cor(x)
r2 = r^2
i = solve(r)
d = diag(i)
p2 = (-i/sqrt(outer(d, d)))^2
diag(r2) <- diag(p2) <- 0
KMO = sum(r2)/(sum(r2)+sum(p2))
MSA = colSums(r2)/(colSums(r2)+colSums(p2))
return(list(KMO=KMO, MSA=MSA))
}
kmo(dados)## $KMO
## [1] 0.5942236
##
## $MSA
## A B C D E F G H
## 0.6789278 0.9151657 0.6897541 0.3385536 0.8699746 0.3632508 0.5172135 0.4878681
## I J K
## 0.4901580 0.4895023 0.4686937Tipos de correlação:
Nem sempre é possível utilizar a correlação de pearson, porém, existem diversas outras maneiras de se saber qual a correlação dos dados. Podemos utilizar correlações como de Spearman, Policórica, etc.. Já fiz um post onde explico os diferentes tipos de relações entre os tipos de variáveis e os tipos de correlações possíveis para avaliar a relação dessas variáveis.
Aqui um outro exemplo de como utilizar a correlação parcial
partial.cor <- function (x)
{
R <- cor(x)
RI <- solve(R)
D <- 1/sqrt(diag(RI))
Rp <- -RI * (D %o% D)
diag(Rp) <- 0
rownames(Rp) <- colnames(Rp) <- colnames(x)
Rp
}
mat_anti_imagem <- -partial.cor(dados[,1:10])
mat_anti_imagem## A B C D E F
## A 0.000000000 -0.25871349 -0.872167400 0.01668860 -0.04245837 -0.011036934
## B -0.258713494 0.00000000 -0.204228090 0.05621580 0.09801359 0.060189694
## C -0.872167400 -0.20422809 0.000000000 -0.02459342 -0.00482831 -0.008201211
## D 0.016688604 0.05621580 -0.024593418 0.00000000 -0.18602037 0.806258927
## E -0.042458373 0.09801359 -0.004828310 -0.18602037 0.00000000 -0.140784264
## F -0.011036934 0.06018969 -0.008201211 0.80625893 -0.14078426 0.000000000
## G 0.006994874 -0.12746560 0.045529480 -0.75073120 -0.32160010 -0.792991683
## H -0.071792191 0.03375700 0.059785980 -0.03196914 0.08903510 0.001496987
## I 0.055698412 -0.03720345 -0.040061304 0.08243832 -0.03925037 0.084673934
## J -0.042609593 0.06775755 0.004145341 -0.06024239 0.05806892 -0.001404078
## G H I J
## A 0.006994874 -0.071792191 0.05569841 -0.042609593
## B -0.127465596 0.033756995 -0.03720345 0.067757550
## C 0.045529480 0.059785980 -0.04006130 0.004145341
## D -0.750731196 -0.031969142 0.08243832 -0.060242391
## E -0.321600101 0.089035097 -0.03925037 0.058068923
## F -0.792991683 0.001496987 0.08467393 -0.001404078
## G 0.000000000 -0.025016441 -0.05943429 0.009961615
## H -0.025016441 0.000000000 -0.55229599 0.044929237
## I -0.059434295 -0.552295987 0.00000000 0.056248550
## J 0.009961615 0.044929237 0.05624855 0.000000000Extração de fatores via componentes principais
Determinado o número de fatores necessários para representar os dados
Também é determinado o método que será utilizado, o mais utilizado é a análise de componentes principais
Estimação do número de fatores m
Estimação do número de fatores m
Para a estimação de m, bastará extrair-se os autovalores da matriz de correlação amostral.
Observa-se quais autovalores são os mais importantes em termos de grandeza numérica.
os autovalores refletem a importância do fator se o número de fatores for igual ao número de variáveis então a soma dos autovetores é igual a soma das variâncias (pois cada variância será igual a 1).
Portanto a razão $ / 2 var $ indica proporção da variabilidade total explicada pelo fator
Critérios:
A análise da proporção da variância total relacionada com cada autovalor (\(\lambda_i\)). Permanecem aqueles autovalores que maiores proporções da variância total e, portanto, o valor de m será igual ao número de autovalores retidos;
A comparação do valor numérico de (\(\lambda_i\)) com o valor 1. O valor de m será igual ao número de autovalores maiores ou iguais a 1.
Observação do gráfico scree-plot, que dispõe os valores de (\(\lambda_i\)) ordenados em ordem decrescente. Por este critério, procura-se no gráfico um “ponto de salto”, que estaria representando um decréscimo de importância em relação à variância total. O valor de m seria então igual ao número de autovalores anteriores ao “ponto de salto”.
Análise de componentes Principais:
Fatores são obtidos através da decomposição espectral da matriz de correlações, resultado em cargas fatoriais que indicam o quanto cada variável está associada a cada fator e os autovalores associados a cada um dos fatores envolvidos
São formadas combinações lineares das variáveis observadas.
O primeiro componente principal consiste na combinação que responde pela maior quantidade de variância na amostra.
O segundo componente responde pela segunda maior variância na amostra e não é correlacionado com o primeiro componente.
Sucessivos componentes explicam progressivamente menores porções de variância total da amostra e todos são não correlacionados uns aos outros.
No R a análise de componentes principais pode ser realizada com as funções nativas prcomp() e a visualização pode ser realizada com a função biplot nativa do R ou com a função autoplot() do pacote ggfortify apresentado em um posto que eu comento sobre ajustes de modelos lineares.
Neste exemplo utilizaremos as funções de código aberto encontrei nesse github que permite elaborar o gráfico baseado em funções do ggplot, além disso também carregaremos o pacote deste Github. Veja:
library(ggplot2)
library(ggfortify)
library(ggbiplot)
#Componentes principais:
acpcor=prcomp(dados, scale = TRUE)
summary(acpcor)## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 1.7205 1.5835 1.2745 1.2107 1.02156 0.72100 0.6634
## Proportion of Variance 0.2691 0.2280 0.1477 0.1333 0.09487 0.04726 0.0400
## Cumulative Proportion 0.2691 0.4971 0.6447 0.7780 0.87285 0.92011 0.9601
## PC8 PC9 PC10 PC11
## Standard deviation 0.4953 0.33061 0.25079 0.14588
## Proportion of Variance 0.0223 0.00994 0.00572 0.00193
## Cumulative Proportion 0.9824 0.99235 0.99807 1.00000ggbiplot(acpcor, obs.scale = 1, var.scale = 1,
ellipse = TRUE, circle = TRUE) +
scale_color_discrete(name = '') +
theme(legend.direction = 'horizontal', legend.position = 'top')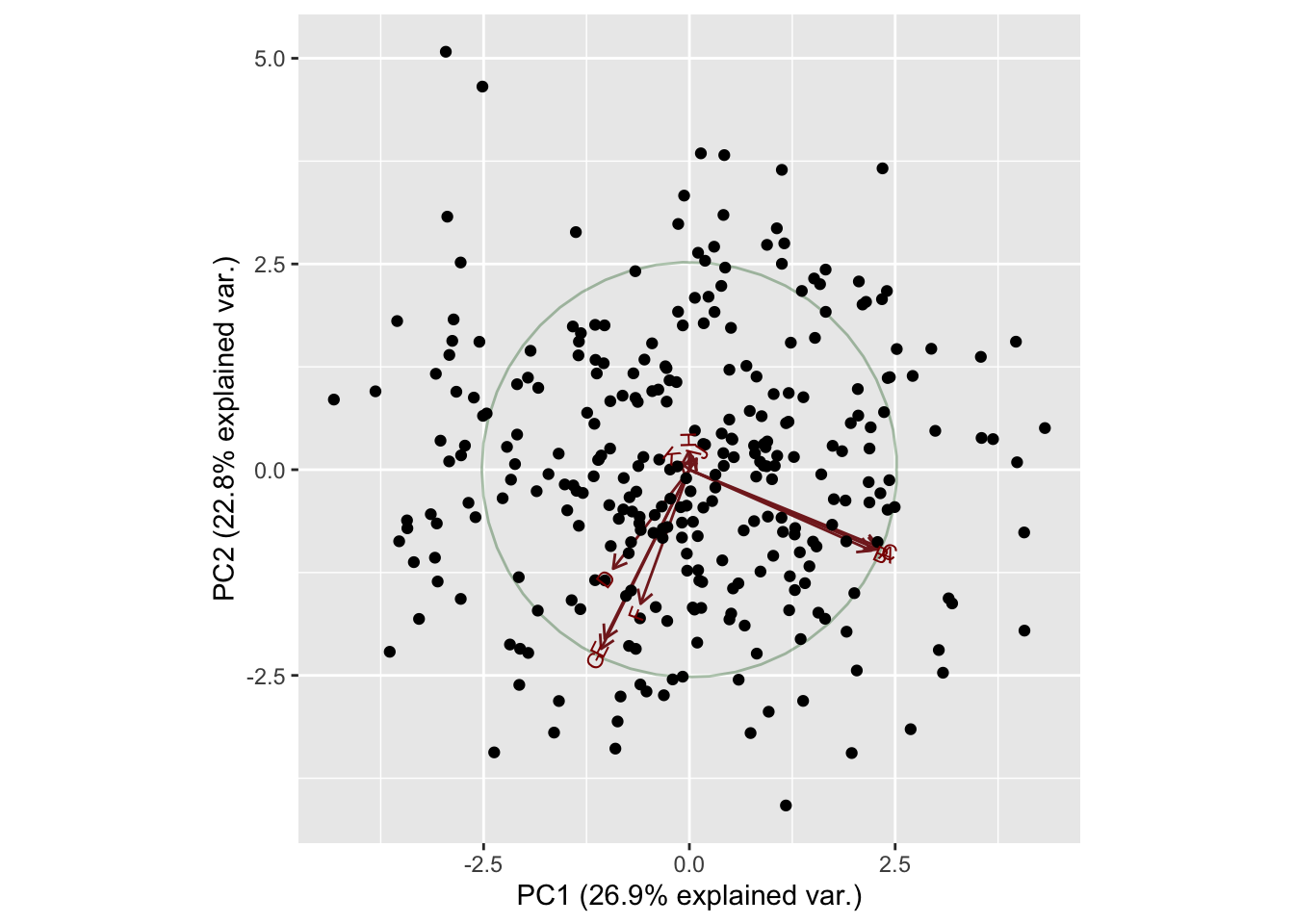
# autoplot(acpcor, label = TRUE, label.size = 1,
# loadings = TRUE, loadings.label = TRUE, loadings.label.size = 3)Para a observação do gráfico scree-plot podemos utilizar os comandos a seguir (com funções nativas do R ou mesmo com funções personalizadas como a que eu acabei de comentar disponivel nesse github
#Com Funcao nativa do R:
# plot(1:ncol(dados), acpcor$sdev^2, type = "b", xlab = "Componente",
# ylab = "Variância", pch = 20, cex.axis = 1.3, cex.lab = 1.3)
#Ou funcao personalizada com ggplot2:
ggscreeplot(acpcor)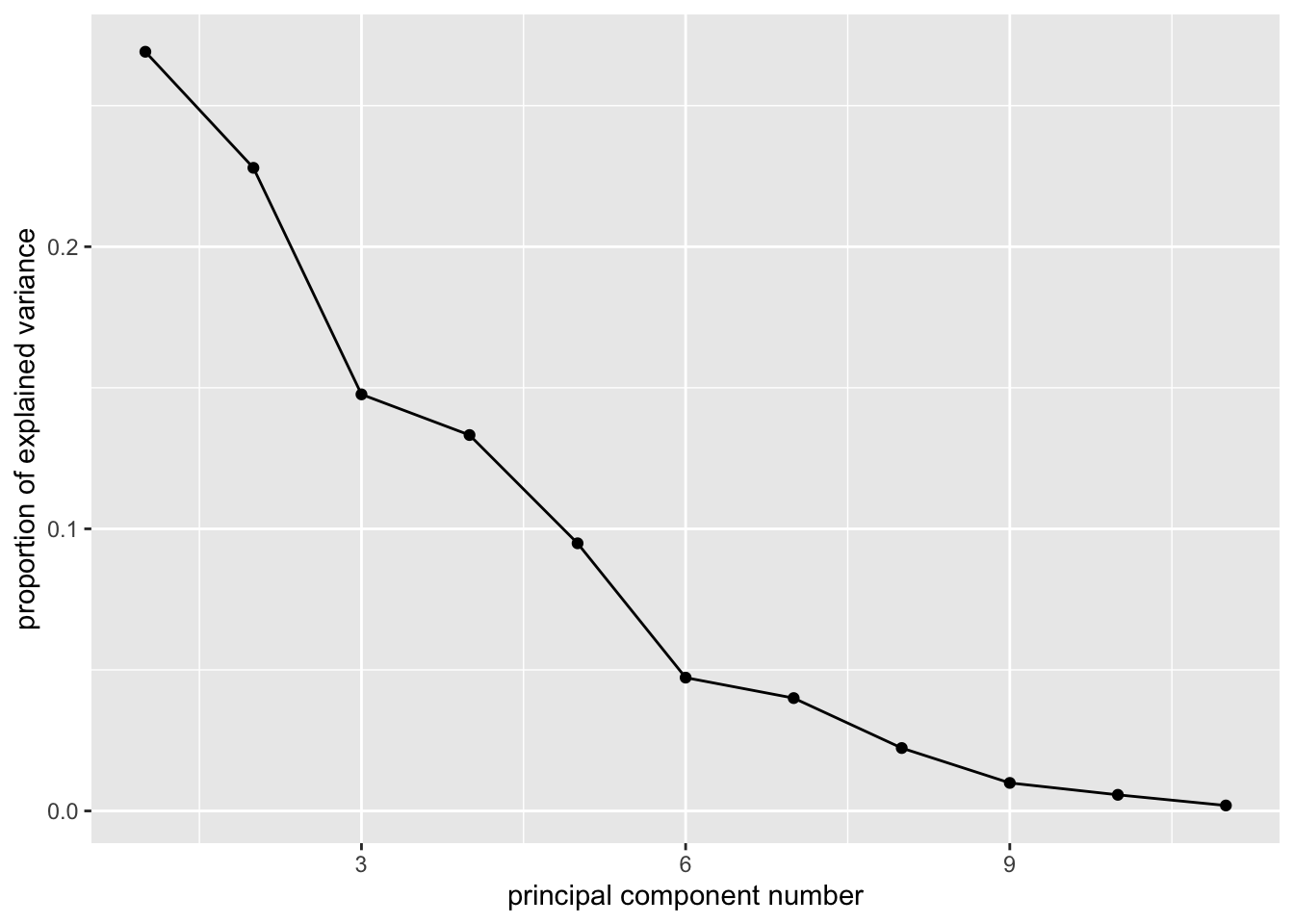
Rotação
Algumas variáveis são mais correlacionadas com alguns fatores do que outras.
Em alguns casos, a interpretação dos fatores originais pode não ser tarefa muito fácil devido à aparição de coeficientes de grandeza numérica similar, e não desprezível, em vários fatores diferentes.
O propósito da rotação é obter uma estrutura simples.
Em uma estrutura simples, cada fator tem carga alta somente para algumas variáveis, tornando mais fácil a sua identificação.
Tipos: Varimax, Quartimax, Equamax
Aplicando a Varimax:
k <- 6 #6 fatores selecionados
carfat = acpcor$rotation[, 1:k] %*% diag(acpcor$sdev[1:k])
carfatr = varimax(carfat)Comunalidade
Índices atribuídos a variável original que expressam em % o quanto da variabilidade de cada variável é explicada pelo modelo
Designa-se por comunalidade (\(h^{2}_i\))a proporção da variância de cada variável explicada pelos fatores comuns.
As comunalidades variam entre 0 e 1, sendo 0 quando os fatores comuns não explicam nenhuma variância da variável e 1 quando explicam toda a sua variância.
Quando o valor das comunalidades é menor que 0,6 deve-se pensar em: aumentar a amostra, eliminar as variáveis.
Interpretar o modelo
Feito pelas cargas fatoriais que são os parâmetros do modelo
Fatores expressam as covariâncias entre cada fator e as variáveis originais
Varimax ajuda a interpretar o modelo
Rotações ortogonais (para dependente) ; Rotações oblíquas (para independentes)
Clusters
Técnica estatística multivariada que tem como objetivo organizar um conjunto de objetos em um determinado nº de subconjuntos mutuamente exclusivos (clusters), de tal forma que os objetos em um mesmo cluster sejam semelhantes entre si,porém diferentes dos objetos nos outros clusters
Etapas para análise de clusters, que são comuns em qualquer análise (KDD):
- Seleção dos objetos a serem agrupados
- Definir conjunto de atributos que caracterizam os objetos
- Medida de dissimilaridade
- Seleção de um algoritmo de agregação
- Definição do número de clusters
- Interpretação e validação dos clusters
Critérios para a seleção:
- Selecionar variáveis diferentes entre si
- Variáveis padronizadas (padronização mais comum é a Z-score)
Existem algumas abordagens para a utilização das técnicas de análises de clusters, as diferenças entre os métodos hierárquicos e os não hierárquicos são as seguintes:
Métodos Hierárquicos são preferidos quando:
- Serão analisadas varias alternativas de agrupamento.
- O tamanho da amostra é moderado ( de 300 a 1000 objetos )
Métodos não-hierárquicos são preferidos quando:
- O número de grupos é conhecido.
- Presença dos outliers, desde que os métodos não-hierárquicos são menos influenciados por outliers.
- Há um grande nº de objetos a serem agrupados.
Método hierárquico de agrupamento
É realizado em dois passos, o primeiro deles calcula-se a matriz de similaridade com o uso da função dist() (existem diversos tipos de distâncias que podem ser utilizadas aqui), o método utilizado será o de Ward (também poderíamos escolher o método da menor distância, maior distância ou a distância média).
Vantagens:
- Rápidos e exigem menos tempo de processamento.
- Apresentam resultados para diferentes níveis de agregação.
Desvantagens:
- Alocação de um objeto em um cluster é irrevogável
- Impacto substancial dos outliers ( apesar do Ward ser o menos susceptível)
- Não apropriados para analisar uma amostra muito extensa, pois a medida que o tamanho da amostra aumenta, a necessidade de armazenamento das distâncias cresce drasticamente
Para bases grandes é melhor não usar este método pois precisa da matriz de distâncias.
Dentre os métodos, a menor distância pode ser ruim em muitas situações, pois coloca muitos objetos no mesmo cluster.
Geralmente utiliza-se o dendograma para a visualização dos clusters.
#Construindo a matriz de similaridade:
matriz_similaridade = dist(iris[,-5], #Conjunto de dados utilizados
"euclidean" #medida de distância utilizada
)
#Construindo o agrupamento hierárquico aglomerativo:
agrupamento = hclust(matriz_similaridade, #Matriz de similaridade calculada
"ward.D" #Método de agrupamento
)
#Converte hclust em dendrograma e plot:
hcd <- as.dendrogram(agrupamento)
library(ggdendro)
# Tipo pode ser "rectangle" ou "triangle"
dend_data <- dendro_data(hcd, type = "rectangle")
# o que esta contido em dend_data:
names(dend_data)## [1] "segments" "labels" "leaf_labels" "class"plot(agrupamento,xlab="Matriz de similaridade",main = "Dendograma", cex = 0.3)
#Construindo representacao de grupos - geração de vetores:
grupos = cutree(agrupamento, #Variável calculada em hclust
3 #Quantidade de grupos desejados
)
#Construindo o dendograma:
rect.hclust(agrupamento, k=3, border="red")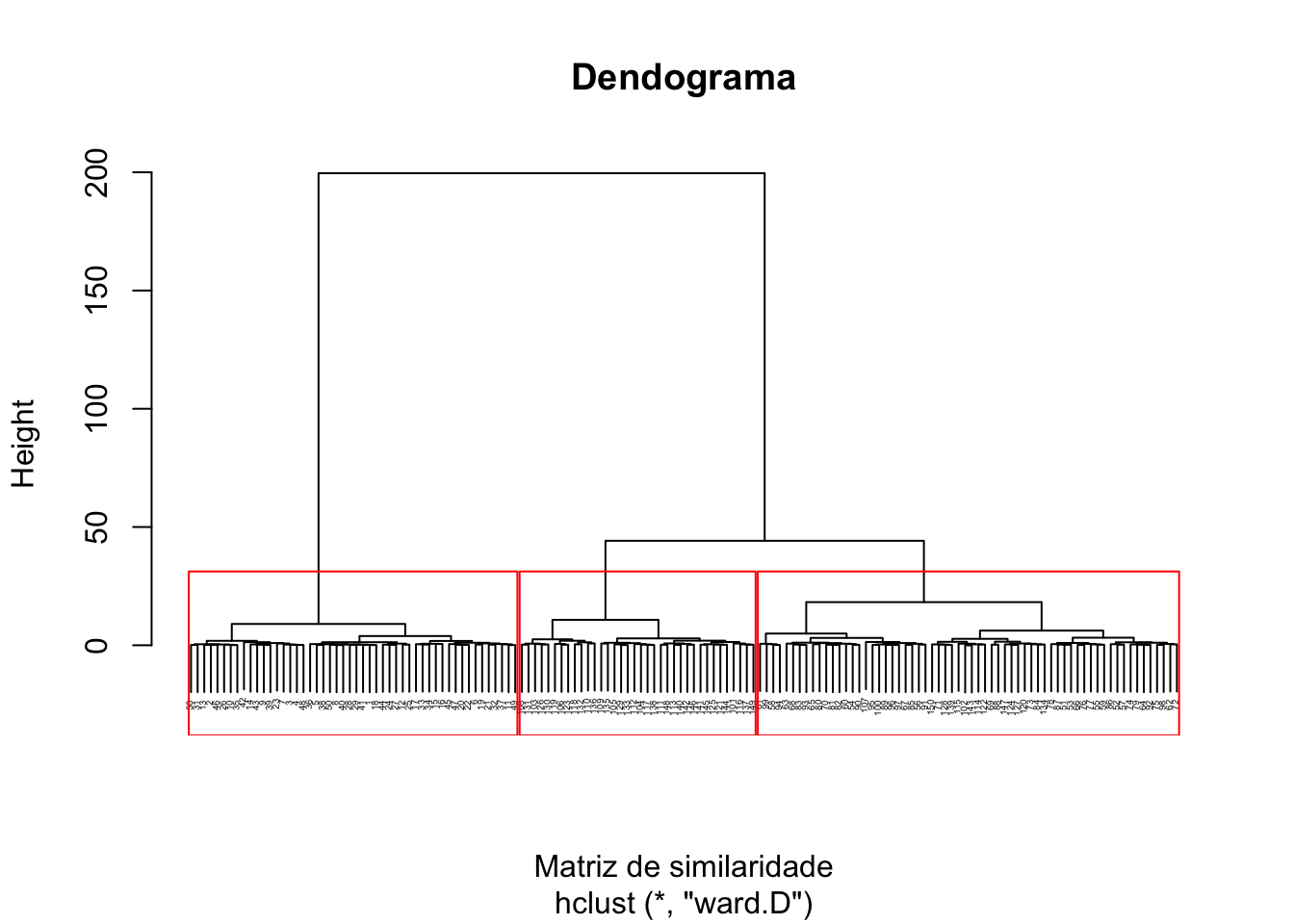
Existem diversas outras maneiras de se visualizar dendogramas, veja a seguir um outro exemplo utilizando o pacote ape:
library(ape)
plot(as.phylo(agrupamento), type = "unrooted", cex = 0.6,
no.margin = TRUE)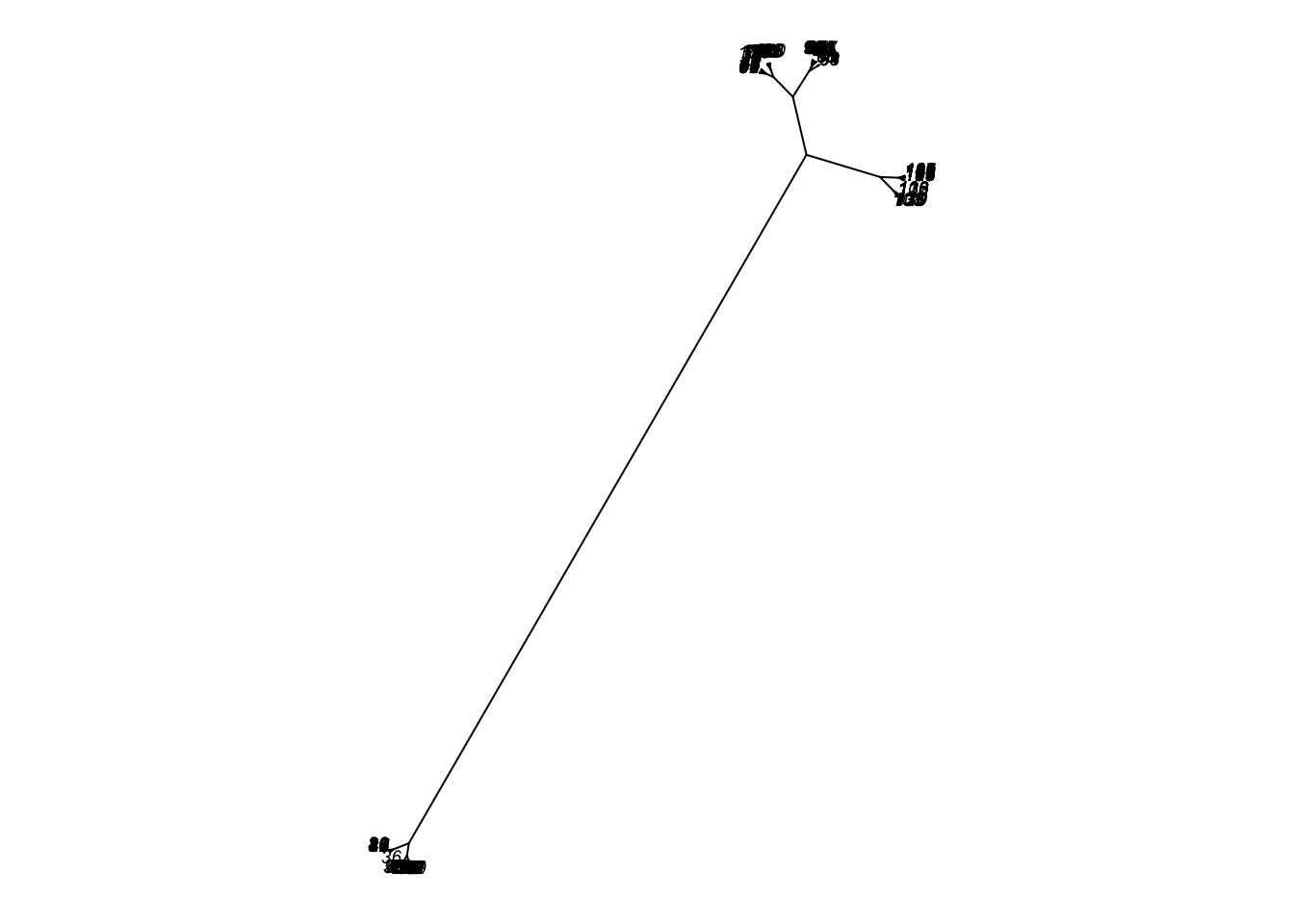
Para mais informações de métodos de plot de dendogramas,talvez essa página possa ser útil.
Método não hierárquico de agrupamento K-means
Esta é uma das mais populares abordagens de agrupamento de dados por partição. A partir de uma escolha inicial para os centroides, o algoritmo procede verificando quais exemplares são mais similares a quais centroides.
Vantagens:
- Tendem a maximizar a dispersão entre os centros de gravidade dos clusters (mantem os clusters bem separados)
- Simplicidade de cálculo, calcula somente as distâncias entre os objetos e os centros de gravidade dos clusters
Desvantagens:
- Depende dos conjuntos de sementes iniciais, principalmente se a seleção das sementes é aleatória
- Não há garantias de um agrupamento ótimo dos objetos
#Construindo o agrupamento por particionamento:
c = kmeans(iris[,-5], #Conjunto de dados utilizados
2, #Número de grupos a ser descoberto
iter.max=5 #Número máximo de iterações permitido no algorítmo
)Para efeito de visualização, podemos utilizar a seguinte função que encontra dois fatores principais a partir da análise fatorial e às utiliza como eixos
plot_kmeans = function(df, clusters, runs) {
suppressMessages(library(psych))
suppressMessages(library(ggplot2))
#cluster
tmp_k = kmeans(df, centers = clusters, nstart = 100)
#factor
tmp_f = fa(df, 2, rotate = "none")
#collect data
tmp_d = data.frame(matrix(ncol=0, nrow=nrow(df)))
tmp_d$cluster = as.factor(tmp_k$cluster)
tmp_d$fact_1 = as.numeric(tmp_f$scores[, 1])
tmp_d$fact_2 = as.numeric(tmp_f$scores[, 2])
tmp_d$label = rownames(df)
#plot
g = ggplot(tmp_d, aes(fact_1, fact_2, color = cluster)) + geom_point() + geom_text(aes(label = label), size = 3, vjust = 1, color = "black")
return(g)
}
plot_kmeans(iris[,-5], 3)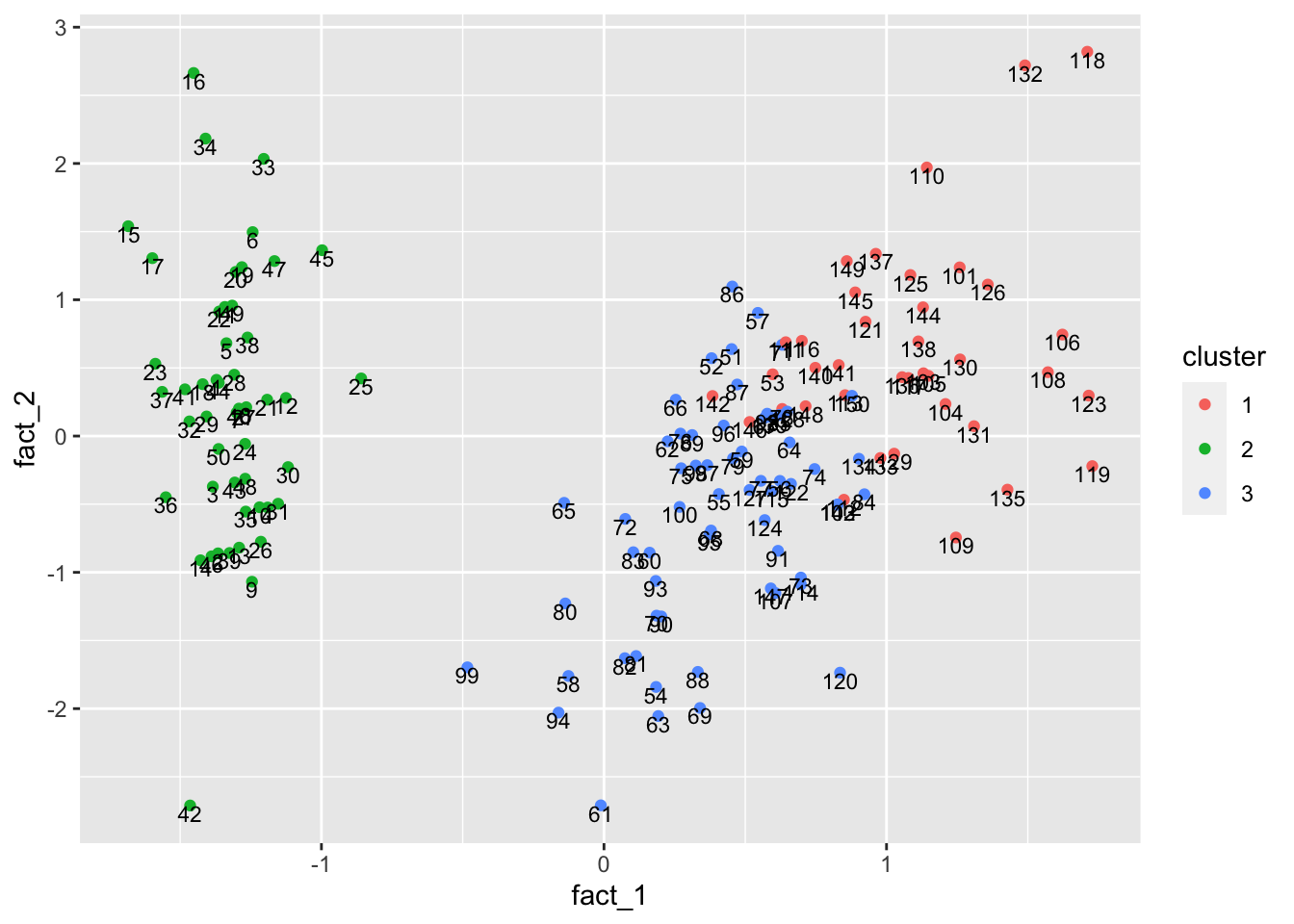
Análise exploratória dos clusters
Não vou me estender nessa parte, mas é bom esclarecer que após encontrar os clusters e de extrema importância realizar a análise exploratória deles para entender os comportamentos dos grupos identificados.
#Conferindo os grupos formados:
c$cluster%>%
table()## .
## 1 2
## 53 97c$cluster%>%
table()%>%
barplot(main="Frequências dos clusters", names.arg=c("Cluster 1", "Cluster 2"))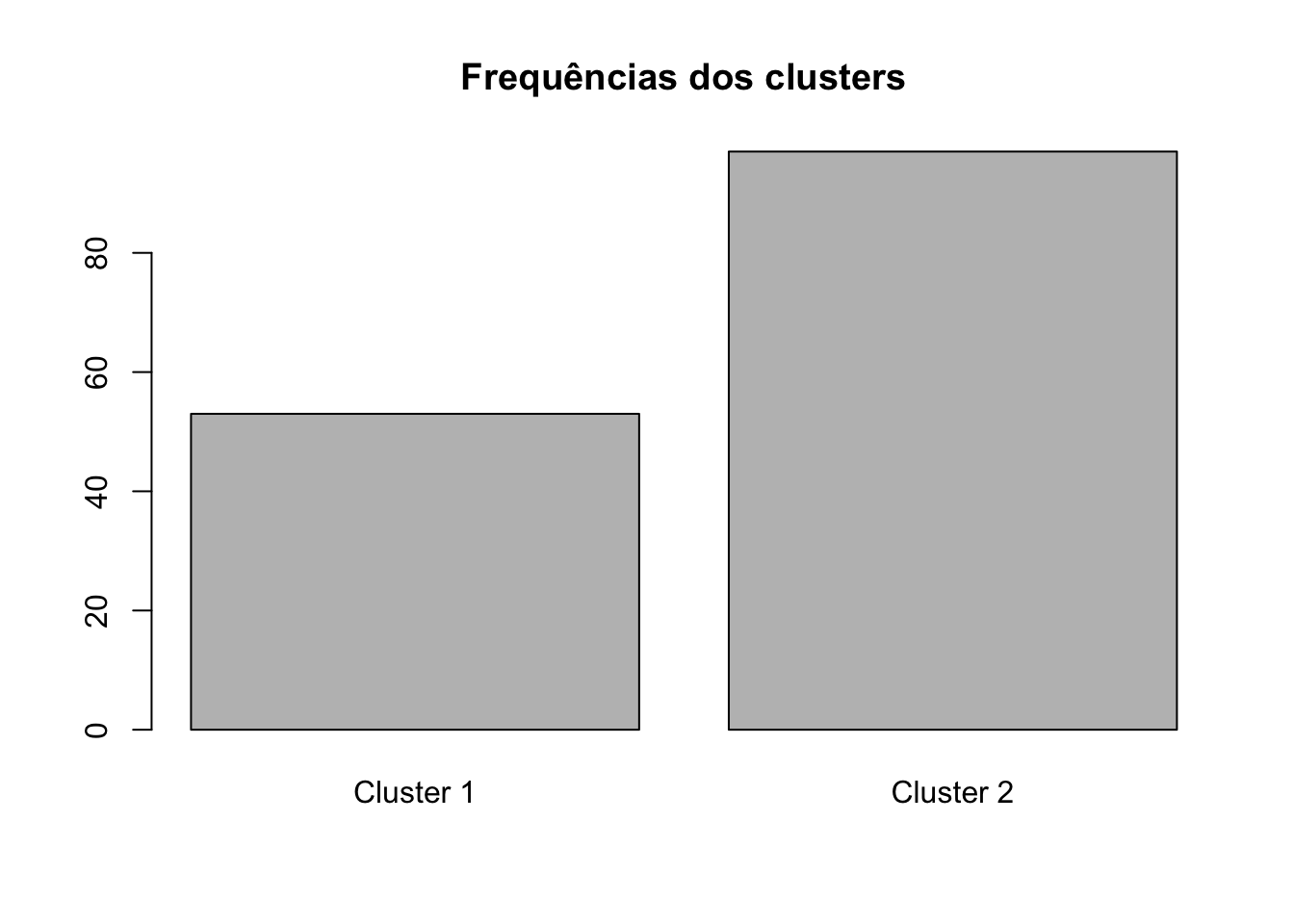
Medidas de validação e estabilidade
pseudo-F
O número adequado de clusters (k) deve ser maximizar o pseudo-F:
\[ pseudo-F = \dfrac{ \dfrac{BSS}{k-1} } { \dfrac{WSS}{N-k}} =\dfrac{\textrm{Quadrado médio entre clusters}}{\textrm{Quadrado médio dentro dos clusters}} \]
library(clvalid)
Este pacote faz os cálculos das medidas que avaliam se os clusters são compactos, bem separados e estáveis.
Vejamos os tipos de medidas:
Medidas de validação:
- conectividade: relativa ao grau de vizinhança entre objetos em um mesmo cluster, varia entre 0 e infinito e quanto menor melhor.
- silhueta: homogeneidade interna, assume valores entre -1 e 1 e quanto mais próximo de 1 melhor.
- índice de Dunn: quantifica a separação entre os agrupamentos, assume valores entre 0 e 1 e quanto maior melhor.
Medidas de estabilidade:
- APN - average proportion of non-overlap: proporção média de observações não classificadas no mesmo cluster nos casos com dados completos e incompletos. Assume valor no intervalo [0,1], próximos de 0 indicam agrupamentos consistentes.
- AD - average distance: distância média entre observações classificadas no mesmo cluster nos casos com dados completos e incompletos. Assume valores não negativos, sendo preferíveis valores próximos de zero.
- ADM - average distance between means: distância média entre os centroides quando as observações estão em um mesmo cluster. Assume valores não negativos, sendo preferíveis valores próximos de zero.
- FOM - figure of merit: medida do erro cometido ao usar os centroides como estimativas das observações na coluna removida. Assume valores não negativos, sendo preferíveis valores próximos de zero.
library(clValid)
#Medidas de validação:
valida=clValid(iris[1:4],3,clMethods=c("hierarchical","kmeans"),validation="internal")
summary(valida)##
## Clustering Methods:
## hierarchical kmeans
##
## Cluster sizes:
## 3
##
## Validation Measures:
## 3
##
## hierarchical Connectivity 4.4770
## Dunn 0.1378
## Silhouette 0.5542
## kmeans Connectivity 10.0917
## Dunn 0.0988
## Silhouette 0.5528
##
## Optimal Scores:
##
## Score Method Clusters
## Connectivity 4.4770 hierarchical 3
## Dunn 0.1378 hierarchical 3
## Silhouette 0.5542 hierarchical 3#Medidas de estabilidade;
valida=clValid(iris[1:4],3,clMethods=c("hierarchical","kmeans"),validation="stability")
summary(valida)##
## Clustering Methods:
## hierarchical kmeans
##
## Cluster sizes:
## 3
##
## Validation Measures:
## 3
##
## hierarchical APN 0.0912
## AD 1.0596
## ADM 0.3680
## FOM 0.4209
## kmeans APN 0.0630
## AD 0.9390
## ADM 0.1131
## FOM 0.3935
##
## Optimal Scores:
##
## Score Method Clusters
## APN 0.0630 kmeans 3
## AD 0.9390 kmeans 3
## ADM 0.1131 kmeans 3
## FOM 0.3935 kmeans 3Gráfico da silhueta:
library(cluster)
#Construindo a matriz de similaridade:
matriz_similaridade = dist(iris[,-5], #Conjunto de dados utilizados
"euclidean" #medida de distância utilizada
)
#Construindo o agrupamento hierárquico aglomerativo:
agrupamento = hclust(matriz_similaridade, #Matriz de similaridade calculada
"ward.D" #Método de agrupamento
)
silhueta =silhouette(cutree(agrupamento,k=3),dist(iris[,-5]))
plot(silhueta,main="")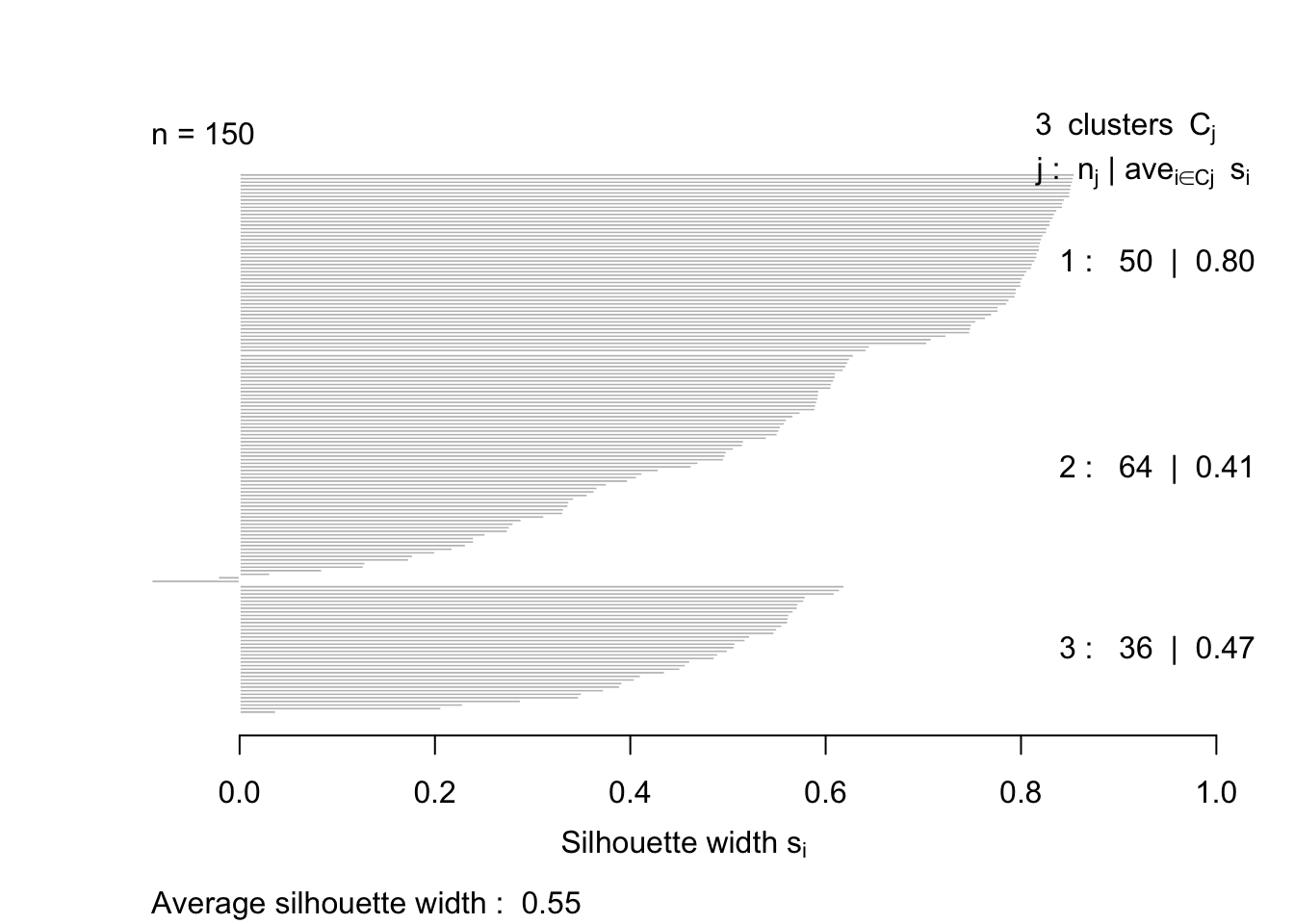
summary(silhueta)## Silhouette of 150 units in 3 clusters from silhouette.default(x = cutree(agrupamento, k = 3), dist = dist(iris[, from -5])) :
## Cluster sizes and average silhouette widths:
## 50 64 36
## 0.7994998 0.4115006 0.4670305
## Individual silhouette widths:
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.09013 0.39933 0.56701 0.55416 0.77690 0.85493Muitas opções
Como podemos observar, a análise de agrupamentos é um método exploratório. É útil para organizar conjuntos de dados que contam com características semelhantes.
É uma das principais técnicas da mineração de dados e já conta com grande variedade de algoritmos.






















Share this post
Twitter
LinkedIn
Email