modelo bayesiano do zero
Um pouco sobre as duas grandes escolas de inferência, contas e implementação de um modelo linear bayesiano na mão para dados simulados e para dados reais
Modelagem estatística e as duas grandes escolas de inferência
Através da modelagem estatística é possível tomar decisões sobre diversos assuntos de interesse como por exemplo na análise de risco de crédito, previsões de quantidade de chuva em um dado local, estimativas de erros ou falhas de um novo produto ou serviço além de diversas áreas como na Educação, Economia, nas Ciências Sociais, Saúde etc.
Muitas vezes os parâmetros das distribuições em estudo podem ser desconhecidos e existe o desejo de se inferir sobre eles. Existem duas grandes escolas de inferência: a clássica e a bayesiana. A clássica trata esses parâmetros como quantidades fixas e não atribui distribuição a eles, a estimação desses parâmetros é dada através da função de verossimilhança, enquanto que na escola bayesiana atribui-se uma distribuição, chamada de distribuição a priori, ao conjunto de parâmetros desconhecidos quantificando a sua crença sobre esse conjunto e a estimação dos parâmetros é dada através da distribuição à posteriori, que é proporcional ao produto da função de verossimilhança com a distribuição a priori.
O interesse pela modelagem estatística através da abordagem bayesiana surgiu a partir de um projeto de iniciação científica quando cursava o 6º período do curso de Graduação em Estatística que tinha como objetivo o cálculo e apresentação de estatísticas descritivas para ajudar uma pesquisadora. Após obter os resultados da análise exploratória e descritiva, notei, junto com meu orientador, que havia possibilidade de dar continuidade ao estudo a partir de uma abordagem estatística mais elaborada. Sendo assim, outro projeto de iniciação científica foi iniciado em seguida com a finalidade de me preparar para utilizar um modelo linear hierárquico bayesiano sob os dados disponibilizados pela pesquisadora em minha monografia.
Caso tenha interesse em conferir o projeto com o estudo sobre modelos hierárquicos bayesianos, disponibilizei os resultados e os códigos em meu github neste repositório. Neste post farei uma breve introdução sobre o ajuste de um modelo linear bayesiano simples e os resultados obtidos (utilizando uma distribuição a priori não informativa). Os resultados obtidos serão comparados com os resultados obtidos com o ajuste de um modelo de regressão linear através da abordagem clássica.
Distribuição a priori
Para o estudo, optou-se pela utilização de valores elevados para variância a priori (também consideradas como “não informativas”, fazendo uma analogia à modelos clássicos) obtendo ajustes que atribuem maior importância à informação provinda da amostra.
Portanto com valores elevados para variância da distribuição a priori (consideradas como “não informativas”) foram obtida a distribuição a posteriori de um parâmetro \(\theta\) que contém toda a informação probabilística a respeito deste parâmetro e quando a forma analítica dessa distribuição é conhecida o gráfico da fdp pode ilustrar o comportamento probabilístico do parâmetro de interesse e auxiliar em alguma tomada de decisão, porém, quando a forma analítica não é conhecida ou é muito custosa de ser obtida, pode-se recorrer a métodos de simulação tais como os métodos MCMC.
Amostrador de Gibbs - método MCMC
Com os avanços dos métodos de MCMC, surgiu o amostrador de Gibbs, proposto por @GemanGeman e tornou-se popular por @GelfandSmith, falo um pouco mais sobre o algoritmo no texto do projeto.
Como a convergência ocorre após o aquecimento (ou burn-in), é comum usar os valores de \(\theta^{(a)}\), \(\theta^{(a+t)}\), \(\theta^{(a+2t)}\),… para compor a amostra de \(\theta\), sendo \(a-1\) o número de iterações iniciais do aquecimento e \(t\) o espaçamento utilizado para diminuir a autocorrelação dos parâmetros. Maiores detalhes podem ser vistos em @Gamerman06.
Ao que interessa
O objetivo deste post é apresentar e comparar os resultados do ajuste de um modelo linear bayesiano simples utilizando uma distribuição a priori não informativa com o modelo de regressão linear simples para dados simulados e para dados reais.
Diversas funções foram criadas ao longo o estudo para conferir o comportamento das cadeias geradas e os resultados do ajuste do modelo, aproveitarei essas funções para este post importando do repositório no github da seguinte maneira:
path_to_dep <- "https://raw.githubusercontent.com/gomesfellipe/projeto_modelos_hierarquicos_bayesianos/master/dependencies.R"
devtools::source_url(path_to_dep, encoding="UTF-8")Ajuste do modelo para dados simulados
Suponha então um exemplo em que a população de interesse tenha distribuição normal com média \(\beta_0 + \beta_1 X\), sendo \(\beta_0\) e \(\beta_1\) desconhecidos e variância \(\sigma^2\) desconhecida. Seja \(\tau=\frac{1}{\sigma^2}\) o parâmetro chamado de precisão.
O parâmetro \(\beta_0\) é conhecido como intercepto ou coeficiente linear e o \(\beta_1\) como coeficiente angular. Além disso, suponha que as unidades dessa população sejam iid. Dessa forma, tem-se que as unidades dessa população tem a seguinte distribuição:
\[ Y_i \stackrel{iid}{\sim} N(\beta_0 + \beta_1 X_i,\frac{1}{\tau}), \]
onde \(i=1,...,N\).
Para o estudo do modelo primeiramente foi utilizado um conjunto de dados simulados utilizando uma amostra de tamanho \(N=1000\) e com os seguintes parâmetros “desconhecidos” dos quais desejamos estimar: \(\beta_0 = 1\), \(\beta_1 = 0,5\), \(\tau = 2\). A amostra será simulada segundo a variável aleatória: \(X_i ~ N(0,1)\) e em seguida os parâmetros deste modelo, denotados por \(\theta = (\beta_0, \beta_1, \tau)\) foram estimados usando o paradigma Bayesiano.
Gerando a amostra
A amostra que foi simulada foi obtida da seguinte maneira:
# Amostra que sera utilizada:
set.seed(12)
n <- 1000 # N=1000
b0 <- 1 # \beta_0 = 1
b1 <- 0.5 # \beta_1 = 0,5
tau <- 2 # \tau = 2 e
x <- rnorm(n) # X_i ~ N(0,1), logo:
y <- b0 + b1 * x + rnorm(n,0,sqrt(1/tau))Obtendo-se uma amostra de tamanho \(n\), pode-se inferir sob os parâmetros desconhecidos \(\theta = (\beta_0, \beta_1, \tau)\) através da distribuição a posteriori e para obter essa distribuição faz-se necessário calcular a função de verossimilhança, que pode ser obtida da seguinte forma:
\[ p(y| \beta_0, \beta_1 , \tau) =\prod^n_{i=1} p(y_i | \beta_0, \beta_1, \tau ) \]
portanto
\[ p(y| \beta_0, \beta_1 , \tau) = \prod_{i=1}^n \frac{ \sqrt{\tau} }{ \sqrt{2\pi} } exp { - \frac{\tau}{2} ( y_i - \beta_0 - \beta_1 x_i )^2 } \]
onde \(y = (y_1, ..., y_n)\) é a amostra coletada. O valor p para o teste de Shapiro para conferir a suposição de normalidade da variável resposta foi de 0.6181791 enquanto que o valor p para conferir a normalidade da variável explicativa foi de 0.7413229.
Distribuição a priori
Durante o estudo diversos valores os parâmetros a priori foram selecionados para que fosse possível avaliar a sensibilidade da qualidade da escolha da distribuição priori, aqui será apresentado os resultados obtidos com valores elevados para variância a priori (também consideradas como “não informativas”, fazendo uma analogia à modelos clássicos) que ajusta o modelo atribuindo maior importância à informação provinda da amostra.
Considere a priori que os parâmetros sejam independentes e que
\[ \beta_0 \sim N(m_0,\sigma_0^2), \\ \beta_1 \sim N(m_1,\sigma_1^2) \mbox{ e } \\ \tau \sim G(a,b). \]
Portanto, para a estimação foram utilizados os seguintes hiperparâmetros : \(m_0 = m_1 = 0\), \(\sigma_0^2 = \sigma_1^2 = 100\), \(a=0,1\) e \(b=0,1\)
No R:
#Parametros para b0 ~ N(mu0, sig0)
mu0 <- 0
sig0 <- 1000
#Parametros para b1 ~ N(mu1, sig1)
mu1 <- 0
sig1 <- 1000
#Parametros para tau ~ G(a,b)
a <- 0.1
b <- 0.1Dessa forma, tem-se que a distribuição conjunta a priori possui a seguinte forma:
\[ p(\beta_0, \beta_1 , \tau) \propto exp\Big\{-\frac{1}{2\sigma_0^2}( \beta_0 - m_0)^2\Big\} exp\Big\{-\frac{1}{2\sigma_1^2}( \beta_1 - m_1)^2\Big\} \tau^{a-1}exp \{-b \tau\}. \]
Distribuição a posteriori
Combinando a função de verossimilhança com a distribuição a priori, obtêm-se a distribuição a posteriori que é proporcional a:
\[ p(\beta_0, \beta_1 , \tau|y) \propto \tau^{\frac{n}{2}+a-1} exp \left\{ -\frac{\tau}{2} \sum^n_{i=1} (y_i - \beta_0 - \beta_1 x_i)^2 - b\tau - \frac{1}{2\sigma_0^2}(\beta_0-m_0)^2 \right\} \times exp\left\{- \frac{1}{2\sigma_1^2}(\beta_1-m_1)^2 \right\} . \]
Note que essa distribuição é multivariada e não possui forma analítica conhecida. Sendo assim, recorre-se aos métodos de MCMC para se obter amostras dessa distribuição. E então faz-se necessário obter as DCCP de \(\beta_0\), \(\beta_1\) e \(\tau\).
Implementando o amostrador de Gibbs
O tamanho da cadeia foi de 30000 simulações e o burn-in (ou amostra de aquecimento) utilizado considerada após o ajuste foi de 15000. no R:
nsim <- 3*10000
burnin <- nsim / 2
cadeia.b0 <- rep(0,nsim)
cadeia.b1 <- rep(0,nsim)
cadeia.tau <- rep(0,nsim)
# Chutes iniciais:
cadeia.b0[1] <- 0
cadeia.b1[1] <- 0
cadeia.tau[1] <- 1Calculos para implementar o algoritimo na mão
Para a implementação do algoritmo, fez-se necessário o cálculo das distribuições condicionais completas a posteriori (DCCP), primeiramente veja os resultados obtidos para \(\tau\):
- DCCP de \(\tau\):
\[ \tau|y_1, ...,y_n,\beta_0, \beta_1 \sim Gama ( \frac{n}{2}+a,b+\frac{1}{2} \sum^n_{i=1}(y_i-\beta_0-\beta_1 x_i)^2 ) \]
Em seguida, veja o resultado obtido para \(\beta_0\), o coeficiente linear da reta, isto é, a altura em que a reta de regressão intercepta o eixo dos \(Y\)’s:
- DCCP de \(\beta_0\):
\[ \beta_0 | y_1,...,y_n , \tau,\beta_1 \sim N(\dfrac{(\tau\sum^n_{i=1}y_i - \tau\beta_1\sum^n_{i=1}x_i +\frac{m_0}{\sigma_0^2})}{ \tau n + \frac{1}{\sigma_0^2}}, (n\tau + \frac{1}{\sigma_0^2} )^{-1}) \]
Por fim, veja o resultado obtido para \(\beta_1\), é o coeficiente angular da reta, ou seja, é o a variação esperada na variável \(Y\) quando a variável explicativa é acrescida de 1 unidade:
- DCCP de \(\beta_1\):
\[ \beta_1 | y_1,...,y_n , \tau,\beta_0 \sim N(\frac{\tau\sum^n_{i=1}x_i y_i - \tau\beta_0\sum^n_{i=1}x_i + \frac{m_1}{\sigma_1^2}}{\tau \sum^n_{i=1}x_i^2 + \frac{1}{\sigma_1^2}}, ( \tau \sum^n_{i=1}x_i^2 + \frac{1}{\sigma_1^2} )^{-1}) \]
Agora que todas as distribuições condicionais completas estão calculadas o algorítimo já pode ser implementado, no R foi feito da seguinte maneira: (note que as linhas que foram comentadas executariam uma barra de carregamento, com ilustrado em seguida)
# pb <- txtProgressBar(min = 0, max = nsim, style = 3) # iniciando barra de processo
for (k in 2:nsim){
#Cadeia tau
cadeia.tau[k] <- rgamma(1, (n/2) + a, b + (sum((y - cadeia.b0[k-1] - (cadeia.b1[k-1]*x))^2)/2))
# Cadeia B0
c0 <- (n*cadeia.tau[k]) + (1/sig0)
m0 <- (cadeia.tau[k]*sum(y) - (cadeia.tau[k]*cadeia.b1[k-1]*sum(x)) + (mu0/sig0))/c0
cadeia.b0[k] <- rnorm(1, m0, 1/sqrt(c0))
# Cadeia B1
c1 <- (sum(x^2)*cadeia.tau[k]) + (1/sig1)
m1 <- ((cadeia.tau[k]*sum(x*y)) - (cadeia.tau[k]*cadeia.b0[k]*sum(x)) + (mu1/sig1))/c1
cadeia.b1[k] <- rnorm(1, m1, 1/sqrt(c1))
# setTxtProgressBar(pb, k)
}# ;close(pb) #Encerrando barra de processo
Resultados da cadeia
A seguir definiremos a variável inds que indica os valores após a amostra de aquecimento (ou burn-in), a variável real que contém os valores reais utilizados para gerar a amostra para conferir se o modelo foi capaz de recuperá-los, os nomes dos parâmetros e os resultados das cadeias foram agregados em uma matriz:
# Juntando resultados:
inds <- seq(burnin, nsim) # Definindo os indices
real <- c(b0, b1, tau)
name <- c(expression(beta[0]), expression(beta[1]), expression(tau))
results <- cbind(cadeia.b0, cadeia.b1, cadeia.tau) %>% as.data.frame() %>% .[inds, ] %T>% headHistograma e densidade
A figura abaixo apresenta os histogramas junto com as densidades de três cadeias obtidas ao se inicializar o amostrador em pontos diferentes de todos os parâmetros contidos em \(\theta\) e uma linha vermelha indicará o valor do real parâmetro utilizado para estimar a cadeia.
g1 <- hist_den(results[,1],name = name[1], p = real[1])
g2 <- hist_den(results[,2],name = name[2], p = real[2])
g3 <- hist_den(results[,3],name = name[3], p = real[3])
grid.arrange(g1,g2,g3,ncol=1)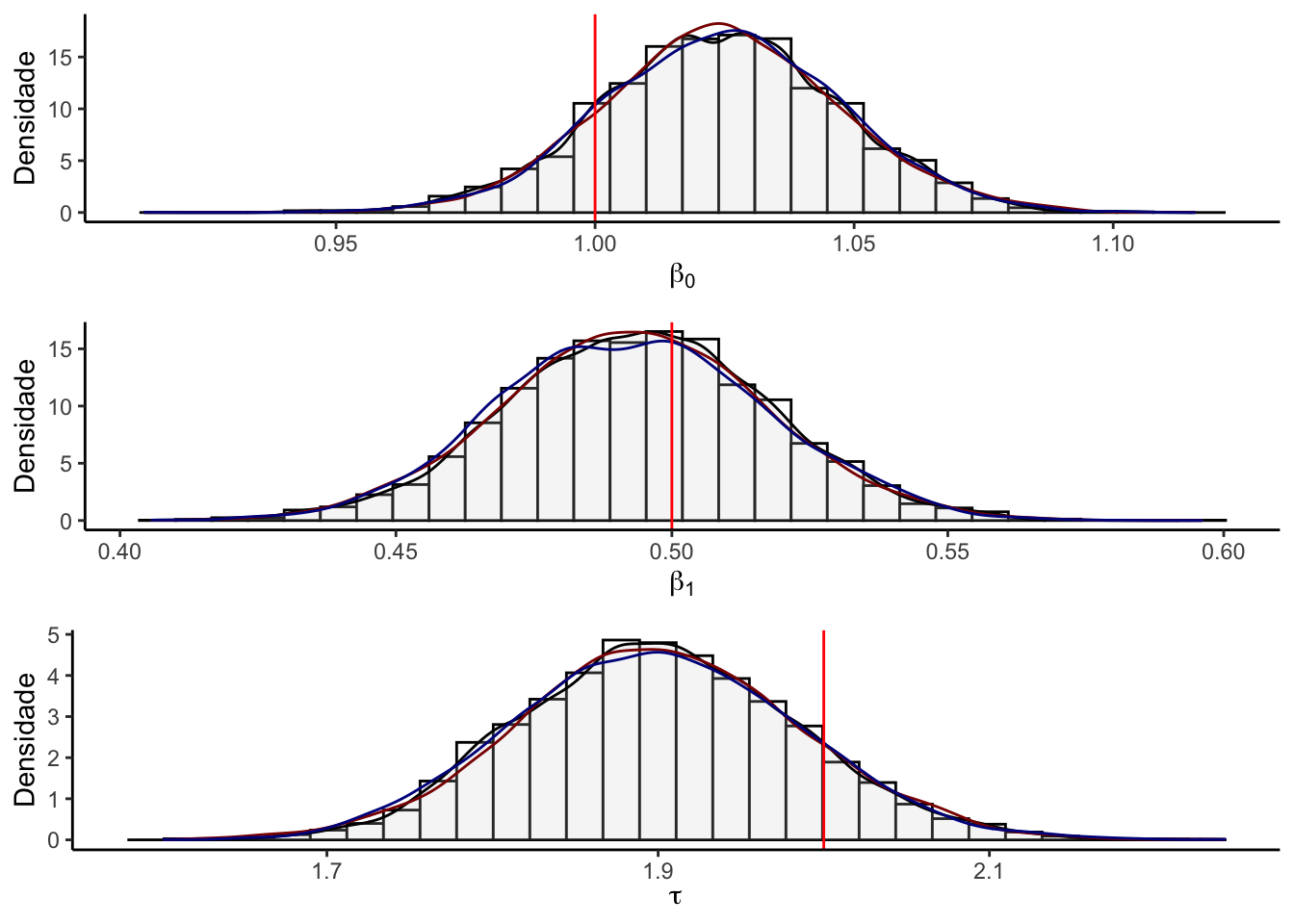
Cadeia
A figura abaixo apresenta os traços das cadeias dos parâmetros amostrados exibindo o intervalo de credibilidade com a linha pontilhada em azul e o valor verdadeiro do parâmetro em vermelho. Note que há indícios de convergência.
# Cadeia
cadeia(results, name, real)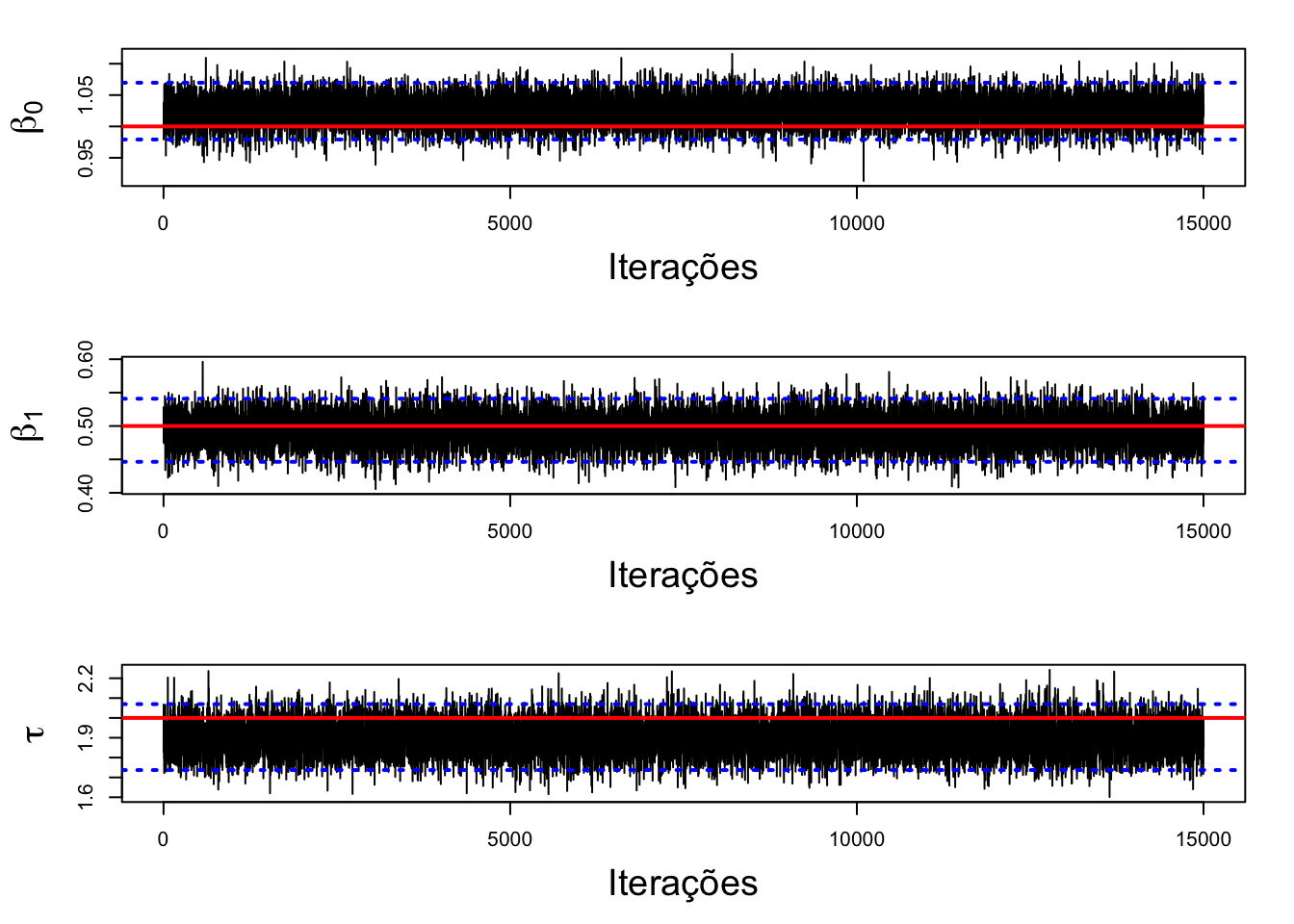
é possível notar que todos os intervalos de credibilidade contêm o parâmetro populacional real utilizado para gerar a amostra.
Autocorrelação
A figura abaixo apresenta os gráficos de autocorrelação, que indicam se houve a influência dos “valores vizinhos” dos parâmetros amostrados. Note que parece haver independência entre as interações.
# ACF
FAC(results)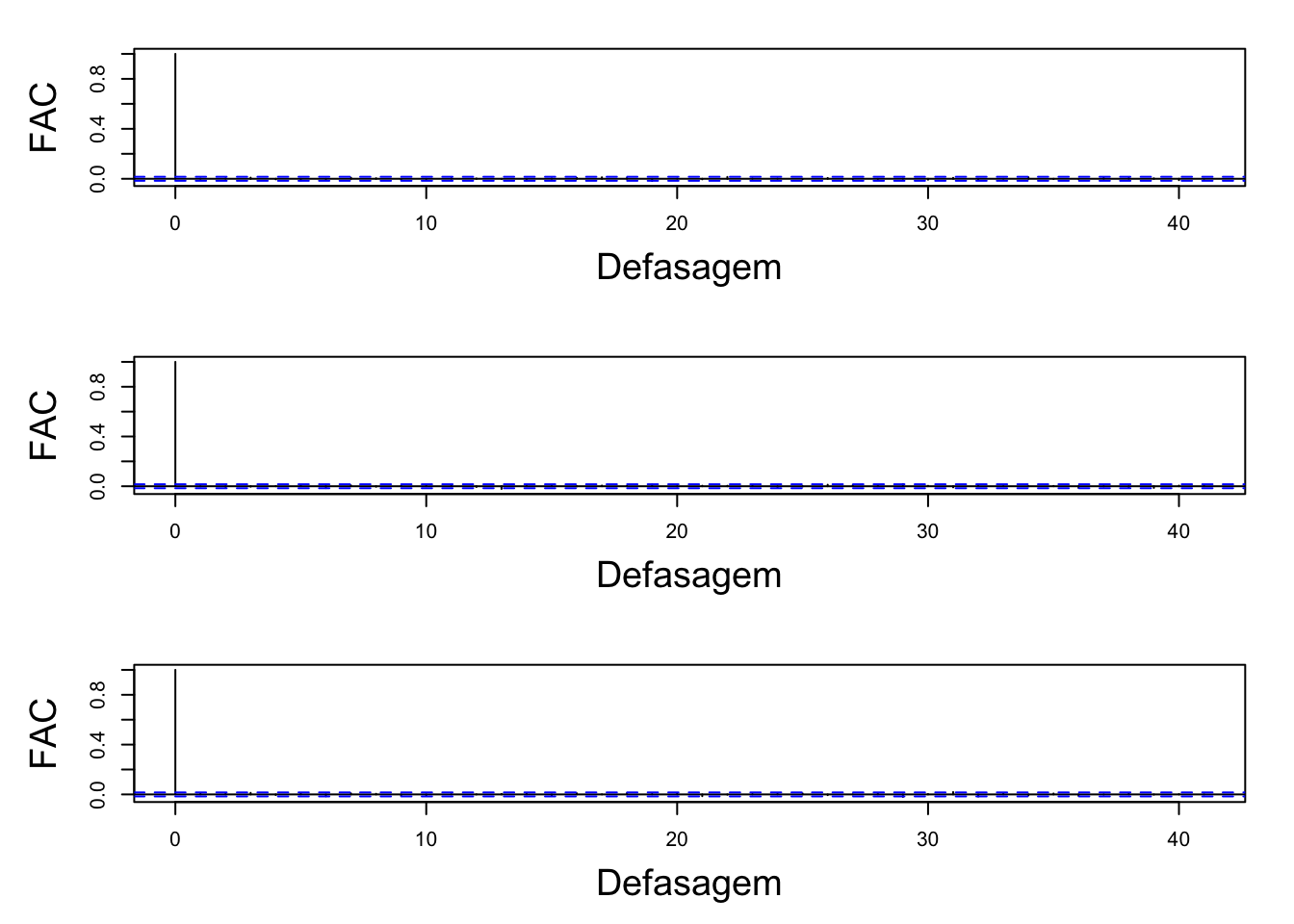
é possível notar que nenhuma das cadeias apresentaram estimativas autocorrelacionada
Estimativas
Agora que já foi verificado que a cadeia se comportou de maneira satisfatória, veja os resultados obtidos sobre as estimativas dos parâmetros através do algoritmo. apresenta os resumos a posteriori dos parâmetros amostrados.
coef <- coeficientes(results, real = real) %>% as.data.frame()
tabela_coeficientes(coef)Como se trata de uma amostra simulada é possível comparar as estimativas com os valores reais que geraram a amostra e os valores estão muito próximos da média (todos eles estão incluídos no intervalo de credibilidade).
Comparando com o modelo linear clássico
Agora que os resultados sob o paradigma bayesiano já foram conferidos será ajustado um modelo de regressão linear simples pelo método dos mínimos quadrados através da função lm() sob o paradigma clássico para comparar com os resultados de um modelo de regressão linear simples sob o paradigma bayesiano utilizando os resultados calculados.
# Reta do modelo classico
plot(x, y)
modelo.classico <- lm(y ~ 1 + x)
a.classico <- modelo.classico$coefficients[1]
b.classico <- modelo.classico$coefficients[2]
abline(a <- a.classico, b = b.classico, col = "blue")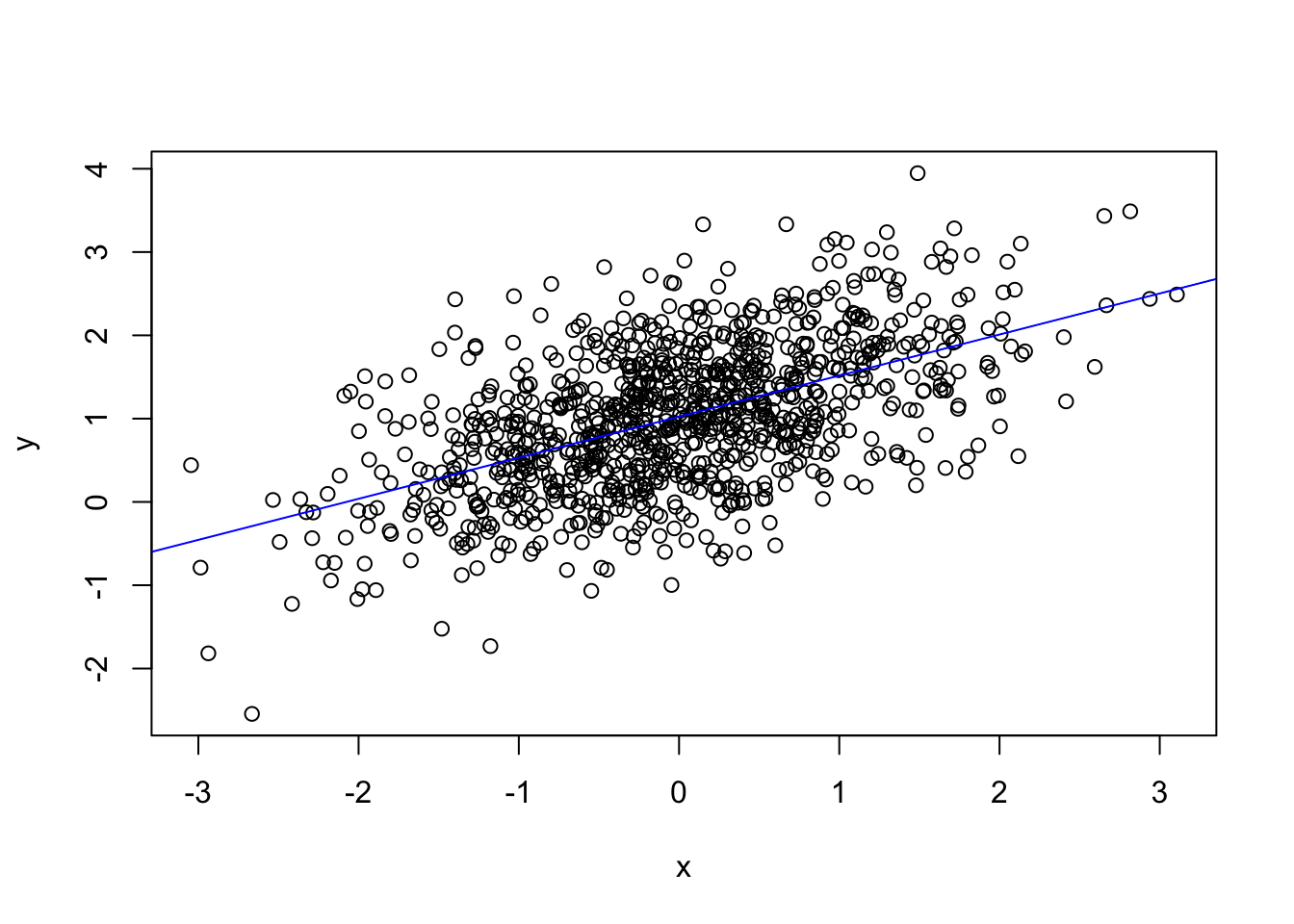
O modelo estimado para estes dados sob o paradigma da inferência clássica foi o seguinte: \(\hat{y} = 1.0245 x + 0,4933\), o que mostra que as estimativas de \(\beta_0\) e \(\beta_1\) foram muito parecidas com as estimativas sob o paradigma da inferência bayesiana.
# Reta do modelo bayesiano
plot(x, y)
a.bayes <- mean(results[, 1])
b.bayes <- mean(results[, 2])
abline(a = a.bayes, b = b.bayes, col = "red")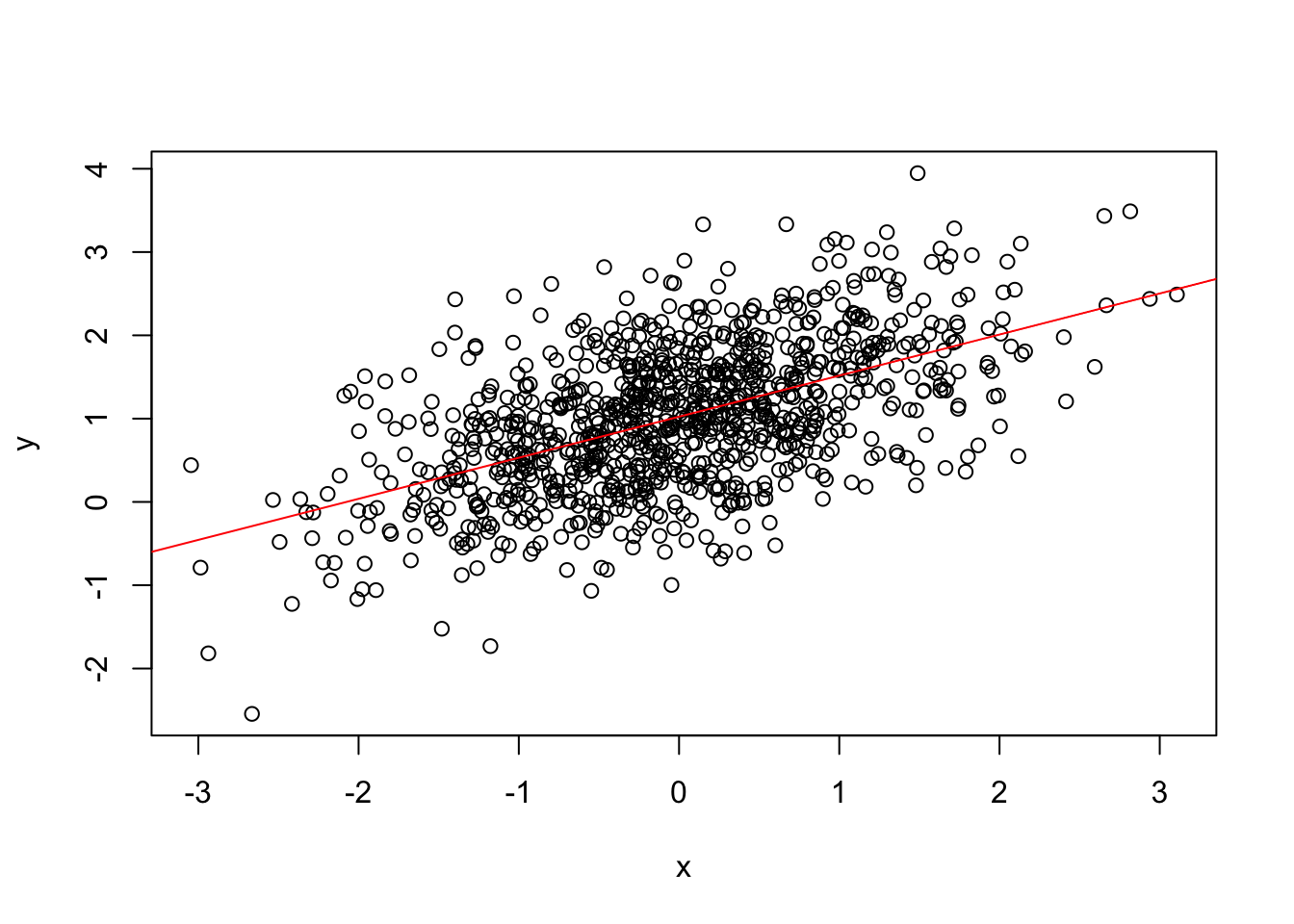
A figura apresenta o gráfico de dispersão entre as variáveis da amostra simulada e as retas dos ajustes de ambos os modelos:
library(stringr)
library(ggplot2)
library(ggExtra)
# Texto da imagem
text.classico <- str_c("Modelo Classico: ","y = ",round(a.classico,4)," x + ",round(b.classico,4))
text.bayes <- str_c("Modelo Bayesiano: ","y = ",round(a.bayes,4)," x + ",round(b.bayes,4))
# Gerando o e ambos:
cbind(y, x) %>%
as.data.frame %>%
ggplot(aes(y = y, x = x)) +
geom_point() +
geom_smooth(method = "lm", se = F, col = "red") +
theme_classic() +
geom_abline(slope = b.bayes,
intercept = a.bayes,
col = "blue") +
labs(title = "",
x = "Covariável",
y = "Reposta")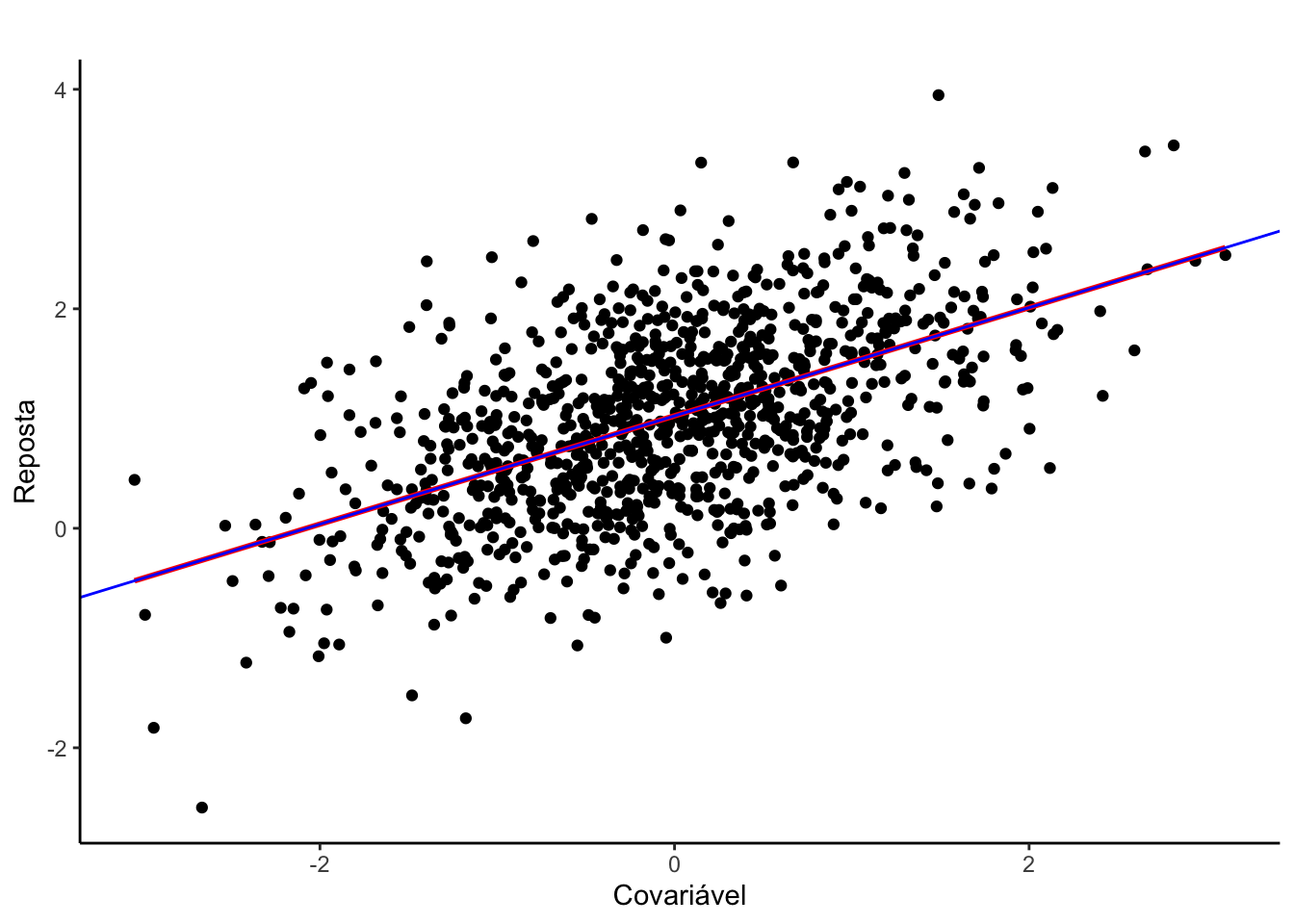
Agora que os resultados no algoritmo já foram conferidos e avaliados de maneira satisfatória utilizando os dados simulados, é a vez de fazer o ajuste para dados reais.
Ajuste do modelo para dados reais
O conjunto de dados que será utilizado como exemplo foi disponibilizado por @Ezekiel_cars e hoje faz parte do conjunto de banco de dados nativos do R (a base de dados pode ser obtida ao escrever cars no console). Os dados informam a velocidade dos carros e as distâncias tomadas para parar, esses dados foram registrados na década de 1920 e são de grande utilidade didática até os dias de hoje.
Considere que deseja-se modelar a velocidade dos carros de acordo com as distâncias tomadas para parar, portanto a variável resposta será a velocidade e a variável explicativa do modelo será a distância tomada para parar.
Amostra utilizada
y <- cars$speed
x <- cars$dist
n <- nrow(cars)o valor p para o teste de Shapiro para conferir a suposição de normalidade da variável resposta foi de 0.4576319 enquanto que o valor p para conferir a normalidade da variável explicativa foi de 0.0390997
Distribuição a priori
Serão utilizados os mesmos valores que foram propostos na simulação como hiperparametros e chutes iniciais para a cadeia, o código usado foi exatamente o mesmo.
Resultados da cadeia
Definiremos novamente a variável inds que indica os valores após a amostra de aquecimento (ou burn-in), desta vez não haverá a variável real pois não conhecemos os valores reais utilizados para gerar a amostra para conferir se o modelo foi capaz de recuperá-los. Desta vez utilizaremos a variável classico, que guarda os valores obtidos com o ajuste do modelo linear pela abordagem clássica.
# Juntando resultados:
inds <- seq(burnin, nsim) # Definindo os indices
results <- cbind(cadeia.b0, cadeia.b1, cadeia.tau) %>% as.data.frame() %>% .[inds, ]
classico <- c(coefficients(lm(cars)), 1 / var(lm(cars)$residuals))
name <- c(expression(beta[0]), expression(beta[1]), expression(tau))Histograma e densidade
A figura abaixo exibe os histogramas com as densidades de três cadeias obtidas ao se iniciar o amostrador em pontos diferentes de todos os parâmetros \(\theta\) mas dessa vez sem a linha vermelha que indicava o valor do parâmetro real pois agora ele é desconhecido.
g1 <- hist_den(results[, 1], name = name[1])
g2 <- hist_den(results[, 2], name = name[2])
g3 <- hist_den(results[, 3], name = name[3])
grid.arrange(g1, g2, g3, ncol = 1)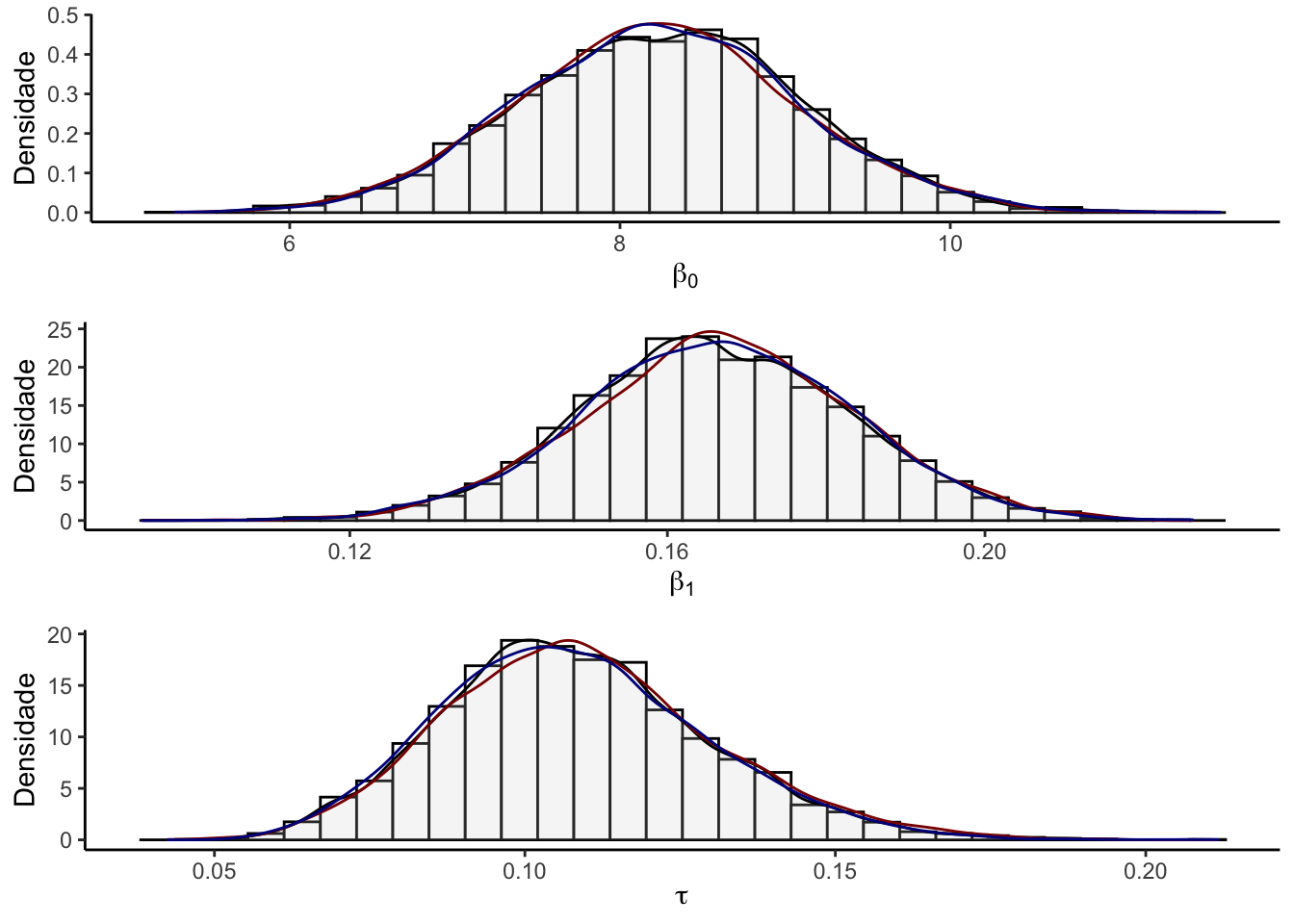
Nota-se que ambas as cadeias convergiram uma mesma distribuição e que as últimas três cadeias apresentaram valores próximos.
Cadeias
A figura abaixo apresenta os traços das cadeias dos parâmetros amostrados. Note que há indícios de convergência.
cadeia(results,name)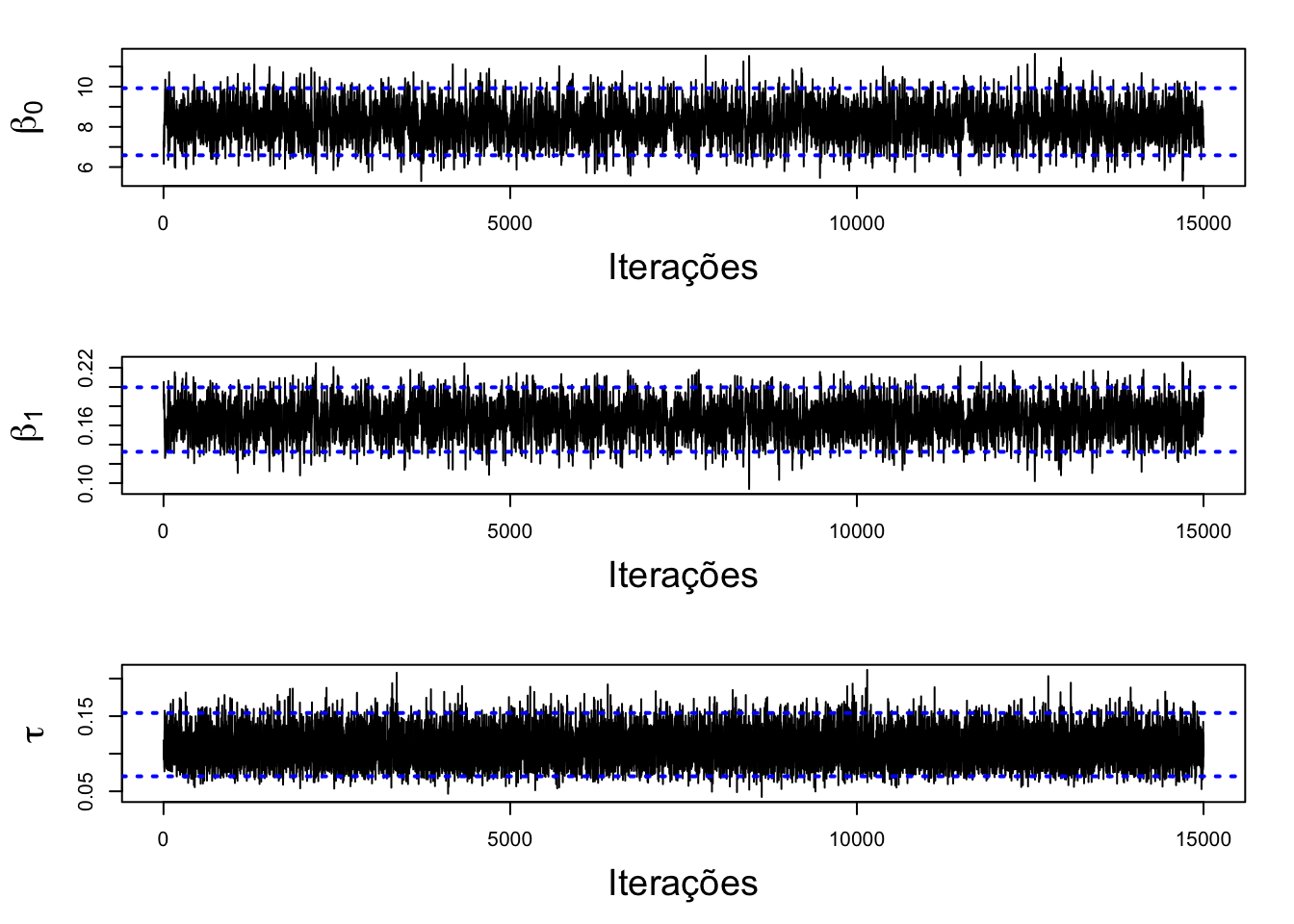
Autocorrelação
A Figura abaixo apresenta os gráficos de autocorrelação dos parâmetros amostrados.
FAC(results)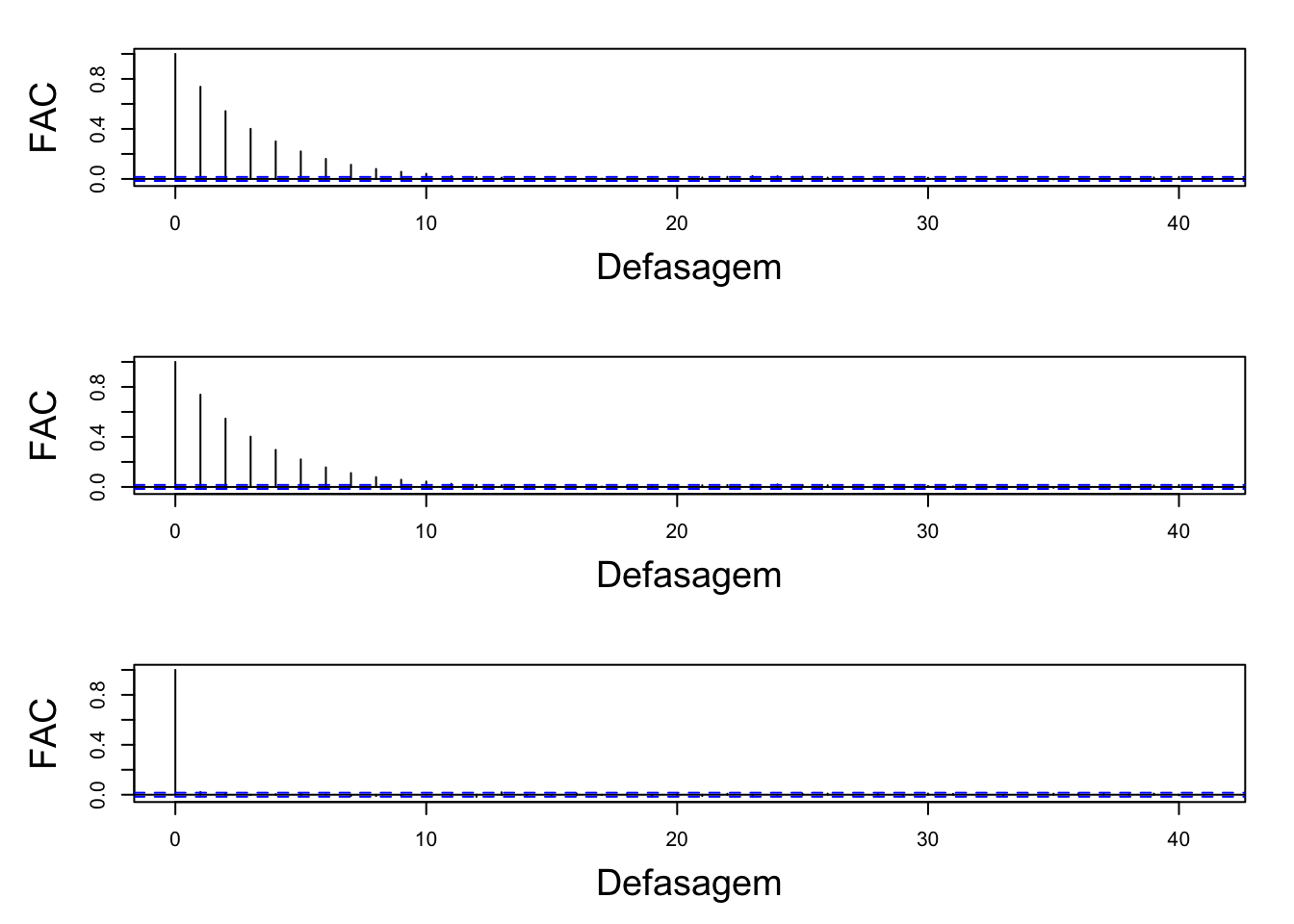
É possível notar que apenas nas primeiras defasagens das cadeias das estimativas para os parâmetros \(\beta_0\) e \(\beta_1\) se apresentaram de forma autocorrelacionada e que a partir dessa defasagem o gráfico de autocorrelação se apresentou de forma desejável.
Estimativas
Como todas as características da cadeia gerada foram avaliadas de maneira satisfatória agora será possível conferir o ajuste dos parâmetros de maneira mais segura pois já foi constatada a convergência da cadeia
Comparando com o modelo linear clássico
Agora que os resultados sob o paradigma bayesiano já foram conferidos novamente será ajustado um modelo de regressão linear simples pelo método dos mínimos quadrados sob o paradigma clássico para comparar com os resultados do um modelo de regressão linear simples sob o paradigma bayesiano utilizando os resultados calculados na seção.
# Reta do modelo classico
plot(x, y)
modelo.classico <- lm(y ~ 1 + x)
a.classico <- modelo.classico$coefficients[1]
b.classico <- modelo.classico$coefficients[2]
abline(a <- a.classico, b = b.classico, col = "blue")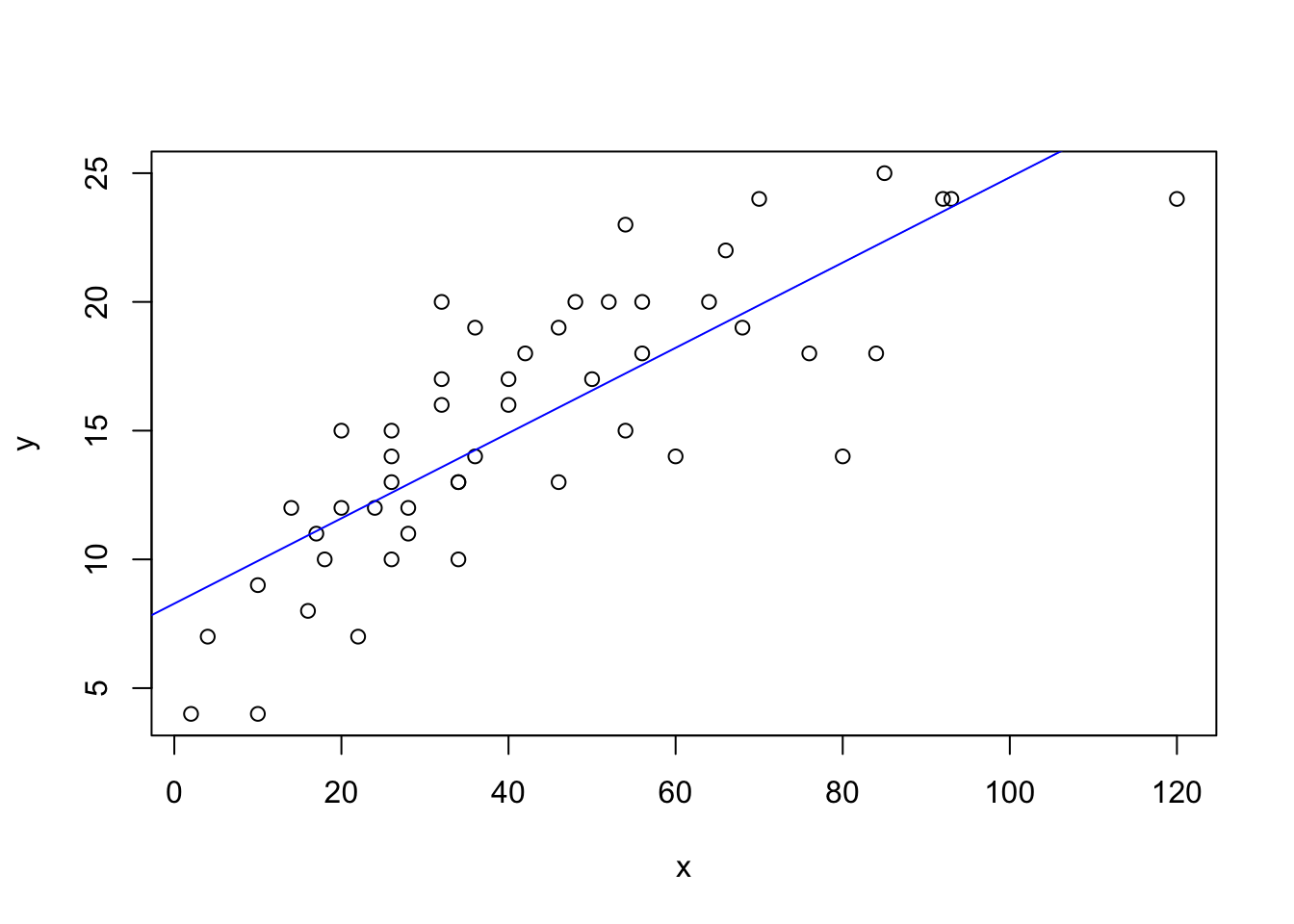
# Reta do modelo bayesiano
plot(x, y)
a.bayes <- mean(results[, 1])
b.bayes <- mean(results[, 2])
abline(a = a.bayes, b = b.bayes, col = "red")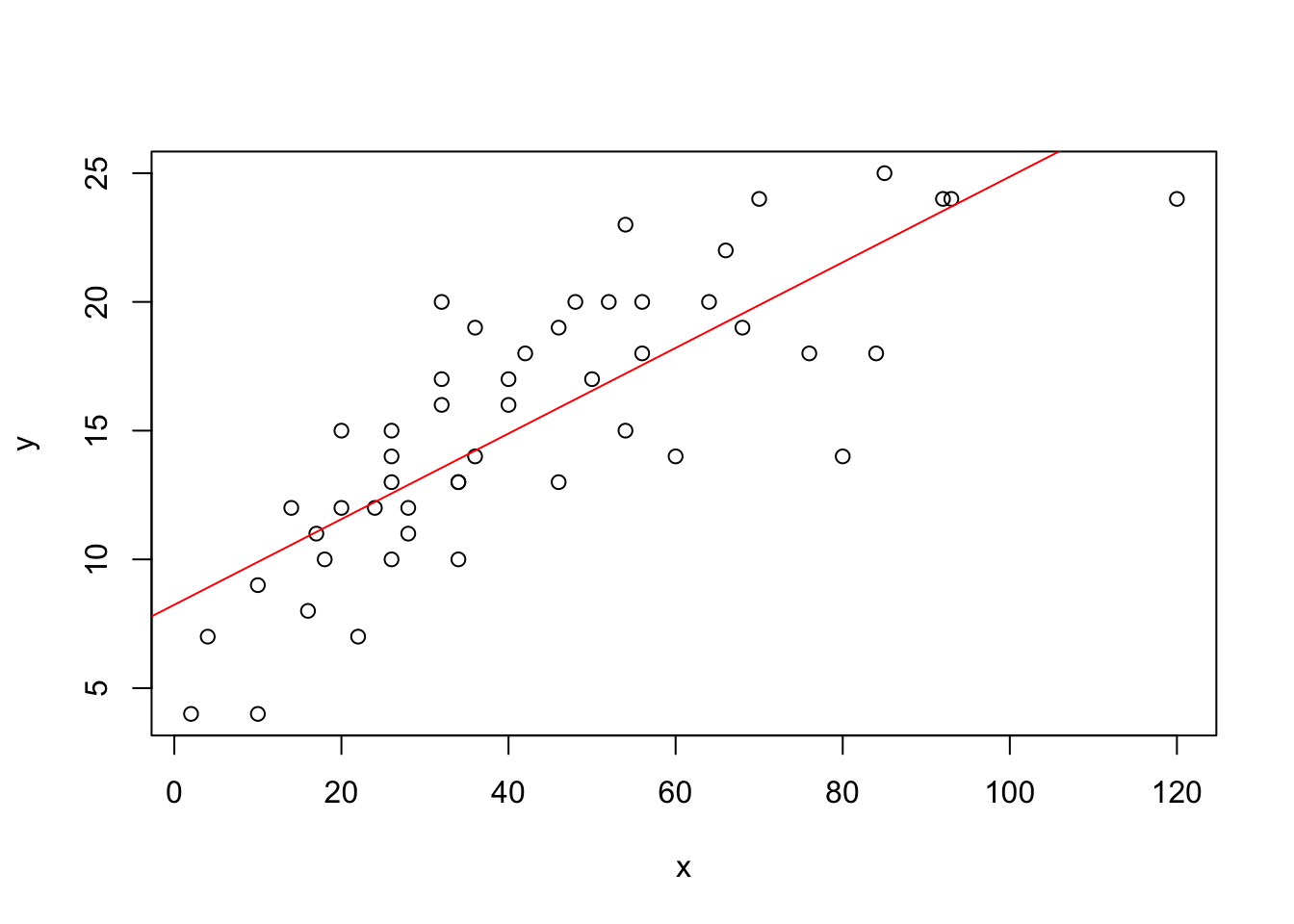
A Tabela abaixo apresenta o resumo a posteriori dos parâmetros estimados da cadeia e note que esta tabela não conta com a coluna dos valores reais como no exemplo anterior e sim as estimativas sob o paradigma clássico.
coef <-
coeficientes(results,real = classico) %>% as.data.frame()
tabela_coeficientes(coef)O modelo estimado sob este paradigma pode ser escrito da seguinte maneira: \(\hat{y} = 8,2839 x + 0,1656\), ou seja, os valores de \(\beta_0\) e de \(\beta_1\) novamente foram muito próximos dos parâmetros obtidos ao estimar sob o paradigma clássico.
Comparando de forma visual
A Figura ilustra o gráfico de dispersão dos dados citados acima, com a intenção de exibir quanto uma variável é afetada por outra, onde no eixo vertical representa a velocidade do carro e no eixo horizontal a distância tomada para parar.
Além do comportamento das variáveis, neste gráfico é exibido também os resultados obtidos do ajuste ao se utilizar o método de mínimos quadrados (representada pela linha em vermelho) para estimar os parâmetros e o ajuste do modelo ao se utilizar o método apresentado acima em (representada pela linha azul).
# Texto da imagem
text.classico <- str_c("Modelo Classico: ","y = ",round(a.classico,4)," x + ",round(b.classico,4))
text.bayes <- str_c("Modelo Bayesiano: ","y = ",round(a.bayes,4)," x + ",round(b.bayes,4))
#Gerando o scatter.plot
cbind(y, x) %>%
as.data.frame %>%
ggplot(aes(y = y, x = x)) +
geom_point() +
geom_smooth(method = "lm", se = F, col = "red") +
theme_classic() +
geom_abline(slope = b.bayes,
intercept = a.bayes,
col = "blue") +
labs(title = "Relação entre a Distância e a Velocidade com \nreta do modelo linear clássico vs bayesiano",
x = "Distância",
y = "Velocidade")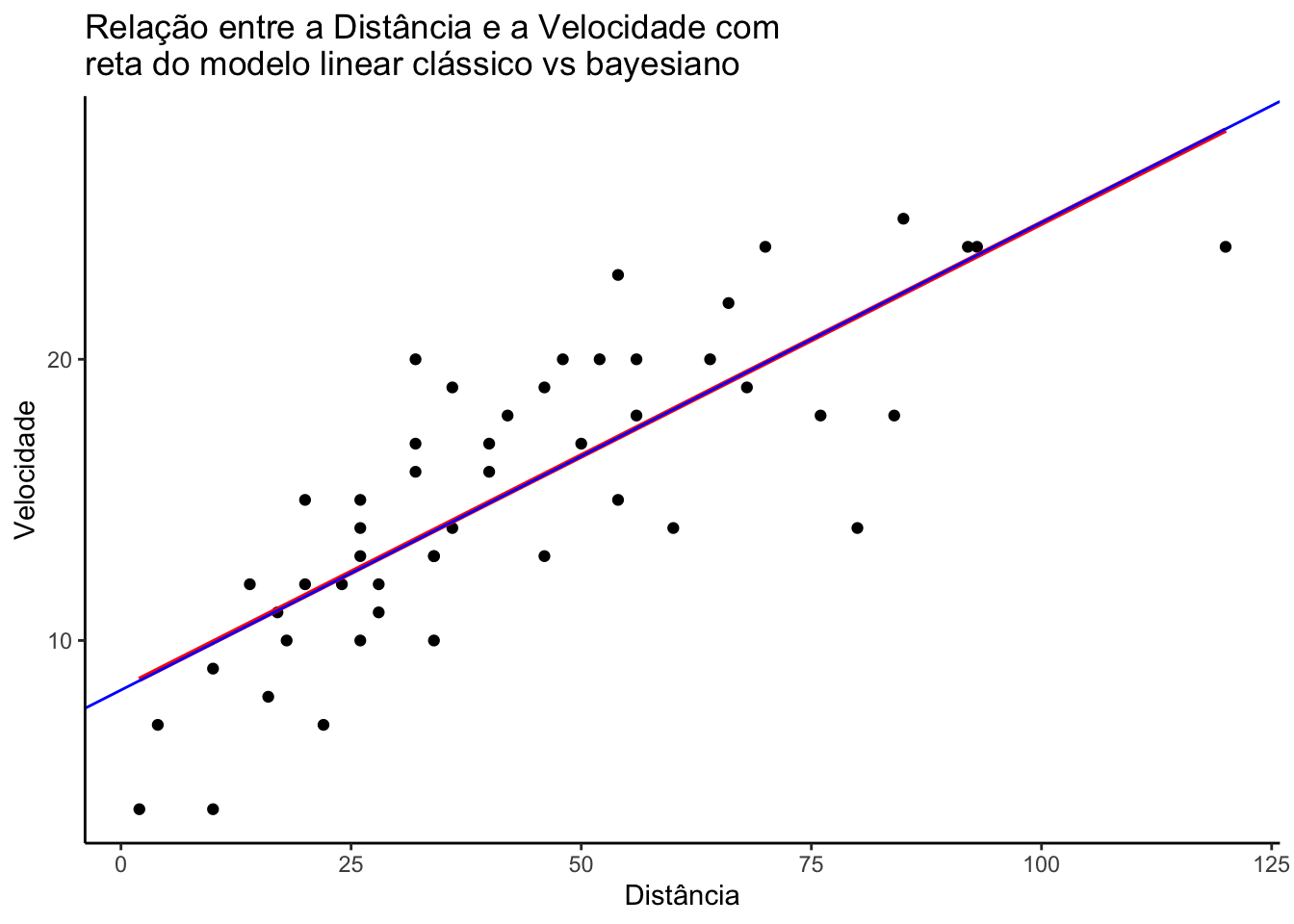
É possível notar que os coeficientes calculados foram muito parecidos, mesmo apresentando pequenas diferenças decimais no valor dos coeficientes ainda é possível notar que as retas estão basicamente sobrepostas, ou seja, os valores estimados em ambas as abordagens foram praticamente os mesmos.
Apesar dos valores dos ajustes terem apresentado basicamente os mesmo resultados, a maneira de se conferir a qualidade do ajuste é diferente em ambas as abordagens. Enquanto sob o paradigma clássico o ajuste do modelo pode ser checado ao avaliar os pre-supostos quanto à distribuição dos resíduos, como recomenda @GaussClarice, ao utilizar um método de MCMC faz-se necessário conferir também outros aspectos como por exemplo se houve convergência da cadeias além do comportamento das autocorrelações, vide @migon.
Conclusão
O uso do algorítmo para simular os dados da implementação do modelo hierárquico bayesiano envolveu diversas etapas. Inicialmente foi necessária a revisão de literatura para a compreensão dos métodos que seriam utilizados na implementação do algoritmo, bem como em seu desenvolvimento. Essa pesquisa funcionou de maneira muito didática, de forma que a cada semana a abordagem pudesse envolver maior grau de complexidade.
Durante o estudo, diversos valores de parâmetros a priori foram selecionados para que fosse possível avaliar a sensibilidade da qualidade da escolha da distribuição a priori. Observou-se que valores elevados para variância a priori (também consideradas como “não informativas” - fazendo uma analogia à modelos clássicos) obtiveram melhores ajustes atribuindo maior importância à informação provinda da amostra.
O estudo com dados simulados facilitou o entendimento do algoritmo pois foi possível notar com facilidade a inadequabilidade das escolhas das prioris, que resultavam em estimativas muito distante do parâmetro populacional que gerou a amostra.























Share this post
Twitter
LinkedIn
Email