Análise de sobrevivência com dados do jogo PUBG disponíveis no Kaggle
O que interefere na probabilidade de um indivíduo sobreviver? Quais fatores apresentam efeito no risco de morte em um intervalo de tempo? Neste post buscaremos evidências estatísticas para responder estas perguntas em dados abertos do PUBG hospedados no Kaggle

Análise de sobrevivência e PUBG
Análise de sobrevivência é um termo que se refere a situações médicas e é caracterizada pela sua variável resposta, que pode ser apresentada de três formas: probabilidade de sobrevivência, taxa de incidêcia e taxa de incidência acumulada.
Na engenharia este termo também é conhecido como confiabilidade, no entanto, condições parecidas podem ocorrer em (inusitadas) outras áreas.
PUBG é um jogo online multiplayer de batalha em que 100 jogadores são lançados em uma ilha e tem como objetivo principal sobreviver, a área de jogo diminui progressivamente, confinando os sobreviventes a um espaço cada vez menor e forçando encontros e o vencedor é o último jogador (ou time) a permanecer vivo.
Um único jogo dura aproximadamente de 30-35 minutos e neste tempo o jogador coleta itens (arma, cura, boost), abate outros jogadores, comete e leva dano de seus adversários, pode dirigir veículos dentre outras ações enquanto tentam sobrevier ao mesmo tempo.
Questões que surgiram em mente após um período de estudos de análise de sobrevivência e confiabilidade e ouvindo pessoas falarem sobre esta modalidade de jogo:
- O que interefere na probabilidade de um indivíduo sobreviver?
- O que tem efeito no risco de um jogador ser abatido em um intervalo de tempo?
Faremos uma abordagem estatística aqui, após uma breve análise exploratória os dados serão avaliados utilizando o modelo de Kaplan-Meier, que é um estimador de forma não paramétrica para a função de sobrevivência e o modelo semiparamétrico de regressão de riscos proporcionais de Cox.
A Base de dados
A base de dados utilizada foi obtida através do Kaggle em “PUBG Match Deaths and Statistics”: https://www.kaggle.com/skihikingkevin/pubg-match-deaths que conta com mais de 65 milhões de registros de mortes no jogo PlayerUnknown Battleground’s matches - PUBG.
Existe uma versão deste post no kaggle e além desta base, existe uma competição em andamento que vai até o dia 30 de Janeiro no link:https://www.kaggle.com/c/pubg-finish-placement-prediction que desafia os jogadores a prever o posicionamento do vencedor em percentil, onde 1 corresponde ao 1º lugar e 0 corresponde ao último lugar do jogo. Fiz uma participação com um script testando os resultados do algorítmo xgboost com caret e também testei uns ajustes com random forest utilizando o tidyverse. Esses scripts são abertos e estão prontos para uso, não me renderam a melhor posição mas a intensão aqui é, principalmente, aprender e testar os métodos pois São muitas possibilidade para aprender e praticar. Voltando a base de dados:
Segundo a descrição da base no kaggle:
agg_match_stats_x.csv fornece informações de correspondência mais agregadas sobre os dados de mortes, como tamanho da fila, fpp/tpp, morte do jogador, etc.
As colunas são as seguintes:
match_id: O id único de correspondência gerado por pubg.op.gg. É possível fazer uma junção disso com os dados das mortes para ver todas as informaçõesparty_size: o número máximo de jogadores por equipe. por exemplo, 2 implica que era um sistema de fila duplaplayer_dist_ride: unidades de distancia total (metros?) que o jogador percorreu em um veículoplayer_dist_walk: unidades de distancia total (metros?) percorrida pelo jogador a pématch_mode: se o jogo foi jogado em primeira pessoa (fpp) ou em terceira pessoa (tpp)team_placement: a classificação final da equipe dentro da partidaplayer_dmg: Total de pontos de vida que o jogador distribuiuplayer_assists: Número de assistências que o jogador marcougame_size: o número total de equipes que estavam no jogoplayer_dbno: Número de knockdowns que o jogador marcouplayer_kills: Número de mortes que o jogador marcouteam_id: o ID da equipe à qual o jogador pertenciadate: a data e a hora em que a partida ocorreuplayer_name: nome do jogador

A rotinas abaixo carregam os pacotes, funções customizadas e salva em extensão .rdsuma amostra da base de dados utilizadas ao longo do post:
# Carregar pacotes --------------------------------------------------------
packages <- c("data.table", "dplyr", "purrr", "survival" , "survminer",
"ggfortify","GGally", "ggplot2","moments", "gridExtra","ggExtra",
"cowplot","lubridate", "scales", "knitr", "kableExtra", "grid",
"broom", "formattable", "grid")
purrr::walk(packages,library, character.only = TRUE, warn.conflicts = FALSE)
rm(packages)
# Funcoes customizadas do github ------------------------------------------
source("https://raw.githubusercontent.com/gomesfellipe/functions/master/inicio_e_fim_da_base.R")
source("https://raw.githubusercontent.com/gomesfellipe/functions/master/grafico_descritivo.R")
source("https://raw.githubusercontent.com/gomesfellipe/functions/master/sumario_custom_num.R")
# Opcoes do documento -----------------------------------------------------
# options(scipen = 99999)
# Tema dos graficos -------------------------------------------------------
theme_set(theme_bw()+
theme(axis.text.x = element_text(size=17),
axis.text.y = element_text(size=17),
axis.title.y = element_text(size=20), legend.position = "bottom"))
# Tema das tabelas kable --------------------------------------------------
kable2 <- function(x,linhas=NULL,colunas=NULL, ...){
k <-
kable(x,digits = 4,...) %>%
kable_styling(bootstrap_options = "striped", full_width = F) %>%
kable_styling(c("striped", "bordered"))
if (!is.null(linhas)) {
# destque na linha:
k <- k %>% row_spec(linhas, bold = T, color = "white", background = "#FFE8BD")
}
if (!is.null(colunas)) {
# destque na colunas:
k <- k %>% column_spec(colunas,bold=T, color="white", background = "#FFE8BD")
}
k %>%
scroll_box(width = "850px")
}Em uma análise de sobrevivência é comum a presença de observações censuradas, (isto é, quando ocorre a perda de informação decorrente de não se ter observado a data de ocorrência do desfecho). No caso dessa base de dados não existe uma variável que define a censura, pois apenas a morte do jogador é registrada e é possível que se os jogadores se desconectarem do jogo mesmo que não sejam mortos seja contado como morte de qualquer jeito. Os detalhes por trás da aquisição de dados não trazem essa informação portanto pode não ser possível distinguir a censura do desfecho e isso é um detalhe relevante que deve ser levado em conta.
# Carregar base -----------------------------------------------------------
set.seed(2) # reprodutivel
pubg_tpp1 <- # Informacoes dos criterios de selecao no corpo do texto
map_df(paste0("agg_match_stats_",0:4,".csv"),
~ fread(.x, showProgress = T,
data.table = T)[match_mode == "tpp" & party_size == 1 & year(date) == 2018 & player_dist_walk>10 & player_dmg != 0 ][, !c("match_mode","party_size","game_size","date", "team_id","player_dbno", "team_placement"), with=FALSE][,player_survive_time := player_survive_time/60] %>%
group_by(match_id) %>%
do(sample_n(.,1)) %>%
ungroup()
)
# Salvar base coletada ----------------------------------------------------
saveRDS(pubg_tpp1,"pubg_tpp1.rds")Descrição da rotina acima e os critérios para a seleção da amostra:
- percorre as 5 bases disponíveis:
paste0("agg_match_stats_",0:4,".csv") - seleciona partidas em terceira pessoa:
match_mode == "tpp" - com tamanho da equipe = 1 (individual):
party_size == 1 - do ano de 2018:
year(date) == 2018 - andaram mais que 10 unidades de distancia (metros?):
player_dist_walk>10 - fizeram algum dano (evitar jogadores ausentes):
player_dmg != 0
- remove colunas não utilizadas na analise
- converte do tempo para minutos:
player_survive_time := player_survive_time/60 - agrupa por partida:
group_by(match_id) - seleciona um jogador de cada partida:
do(sample_n(.,1))
Note que apenas um jogador de cada partida é selecionado na intenção de obter independência entre observações, isso reduziu drasticamente seu tamanho. Agora que a base já foi importada e filtrada, faremos a leitura de 200 linhas aleatórias com a finalidade de diminuir o tempo computacional das operações realizadas em seguida.
set.seed(1)
pubg_tpp1 <- readRDS("pubg_tpp1.rds") %>% sample_n(200)%>%
select(-one_of(c("match_id", "player_name")))Veja a seguir de forma visual como as variáveis numéricas se correlacionam:
pubg_tpp1 %>%
rev %>%
grafico_descritivo()
Variável resposta
Vejamos o que acontece ao analisar o tempo de sobrevivência de cada jogador
A seguir, a distribuição da variável resposta player_survive_time :
plot_grid(pubg_tpp1 %>%
ggplot(aes(x=player_survive_time))+
geom_histogram(aes(y = ..density..), bins = 30, fill="white", color="black")+
geom_density(alpha=.2, fill="white")+
scale_x_continuous(labels = scales::comma, limits = c(0,40), breaks = seq(0,40,5))+
labs(x="",y="", title = "Tempo de sobrevivência dos jogadores selecionados")
,
pubg_tpp1 %>%
ggplot(aes(x=" ", y=player_survive_time))+
geom_boxplot()+
labs(x="")+
coord_flip()
,
ncol = 1, nrow = 2, align = "v", rel_heights = c(3,1))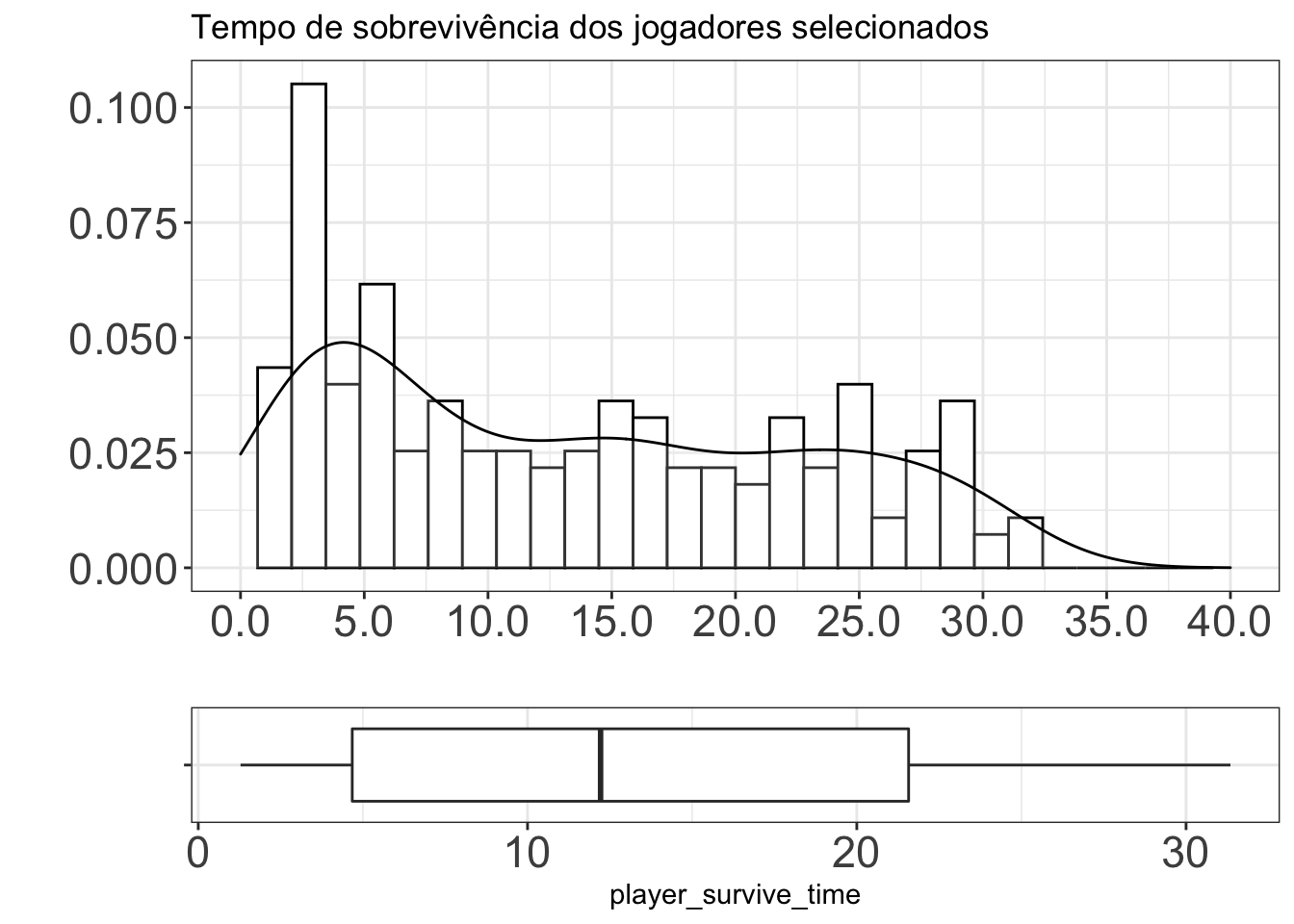
Note que possue uma assimetria positiva
Data Wrangling
Primeiramente, vejamos as variáveis se relacionam entre si e com a variável resposta com os coeficientes de correlação de Pearson:
# Correlations
pubg_tpp1 %>%
select_if(is.numeric) %>%
cor() %>%
corrplot::corrplot(method = "number",type = "upper",diag = F, order = "hclust",number.cex = 0.7, title = "Correlation correlated numerics", mar=c(0,0,1,0))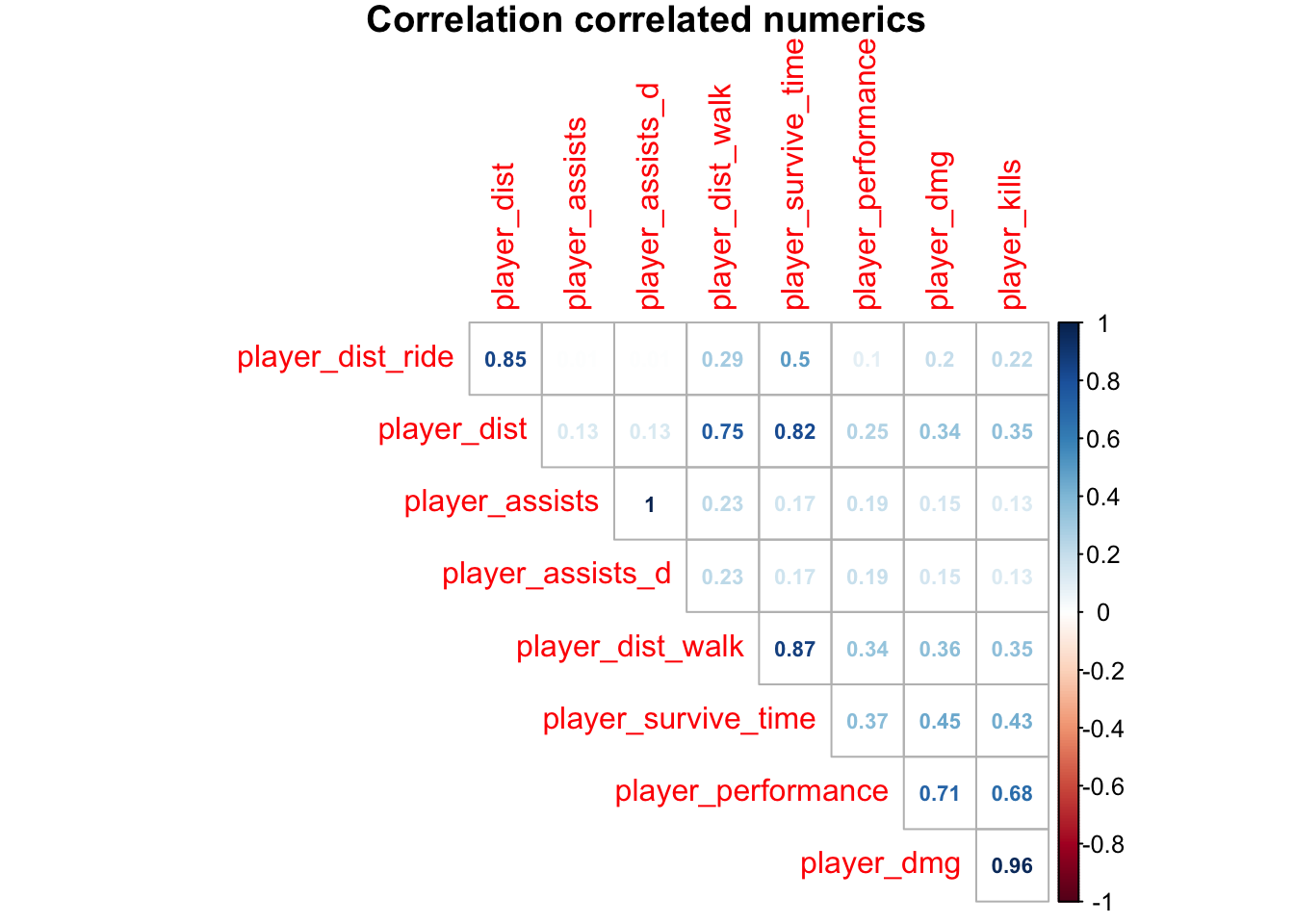
É possível notar que apenas a variável player_assists não correlaciona-se com a variável resposta nem com as demais variáveis e player_dmg e player_kills são fortemente correlacionadas, isso indica que pode ser interessante remover uma delas ou juntar toda essa informação em uma única variável, veremos…
Além disso nota-se que a distância percorrida a pé é fortemente correlacionada com a variável resposta enquanto que a distância de quem andou de carro não é tão correlacionada. Uma transformação na variável player_dist_ride para uma dummy drive indicando se o indivíduo dirigiu ou não pode representar melhor esta informação.
Vejamos algumas características peculiares:
pubg_tpp1 %>%
select(player_kills, player_dist_ride, player_assists) %>%
map_dfr(~quantile(.x, probs = seq(0,1,0.25)) %>% round(2)) %>%
t %>% tidy() %>%
`colnames<-`(c("variável",percent(seq(0,1,0.25)))) %>%
kable2()Praticamente metade da amostra não registrou abates nem possui marcação de player_dist_ride. Como a variável player_dmg apresentou correlação com a variável resposta player_survive_time, vamos fazer algumas transformações:
- Criar uma variável dummy
drivese jogador usou carro - Somar a
player_dist_rideeplayer_dist_walkem uma única variável:player_dist - Juntar
player_kills,player_dmgeplayer_assistsem uma única variável:player_performance
Player performance
Como criar a variável player_performance?
Tentei inventar uma metodologia e com certeza devem existir maneiras mais eficientes de se fazer isso, porém, deixa eu explicar o que eu pensei, considere a formula:
\[ Playerperformance = log(WPlayerDmg + WPlayerAssists + WPlayerKills) \]
onde:
\[ WPlayerKills = log(PlayerKills+0.5)\\ WPlayerDmg = log(PlayerDmg)\\ WPlayerAssists = PlayerAssists \]
Note que:
- \(WPlayerAssists\): Não é feita qualquer transformação;
- \(WPlayerDmg\): A distribuição fica “quase simétrica” após a transformação log;
- \(WPlayerKills\): adiciona-se 0.5 para poder tirar o log pois podem existir zeros nessa variável e além disso, quem não marcou abate será penalizado com \(-1\) na soma final do score:
player_performance.
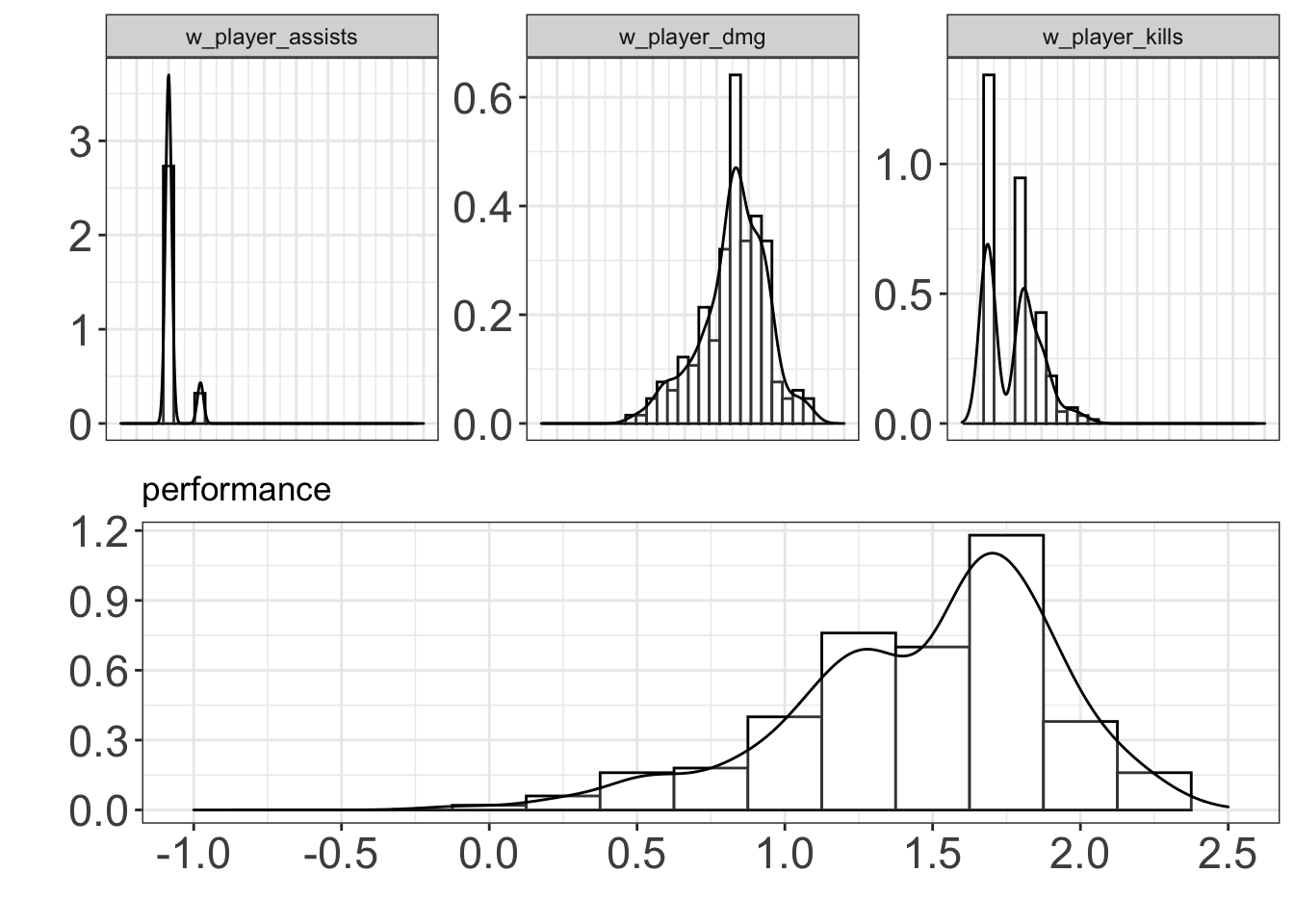
Veja a seguir de forma visual a distribuição das variáveis que farão parte da variável player_performance na parte de cima e na parte inferior o que acontece após sua soma, gerando a nova variável player_performance :
performance <- tibble(w_player_kills = log(pubg_tpp1$player_kills+0.5),
w_player_dmg = log(pubg_tpp1$player_dmg),
w_player_assists = pubg_tpp1$player_assists) %>%
mutate(player_performance = log(w_player_dmg + w_player_assists + w_player_kills))
grid.arrange(
performance %>%
select(-player_performance) %>%
tidyr::gather() %>%
ggplot(aes(x=value))+
geom_histogram(aes(y = ..density..), bins = 30, fill="white", color="black")+
geom_density(alpha=.2, fill="white")+
scale_x_continuous(labels = scales::comma, limits = c(-1.5,8), breaks = seq(-1,8,1))+
labs(x="", y="")+
theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank())+
facet_wrap(~key, scales = "free")
,
performance %>%
select(player_performance) %>%
tidyr::gather() %>%
ggplot(aes(x=value))+
geom_histogram(aes(y = ..density..), fill="white", color="black",bins = 15)+
geom_density(alpha=.2, fill="white")+
scale_x_continuous(limits = c(-1.,2.5), breaks = seq(-1,3,0.5))+
labs(x="", y="", title = "performance"),
ncol=1
)
Transformações na base
A seguir faremos as mudanças diretamente no dataset que estamos trabalhando:
pubg_tpp1 <-
pubg_tpp1 %>%
mutate(player_dist = log(player_dist_ride + player_dist_walk)) %>%
mutate(player_assists_d = if_else(player_assists ==0, 0, 1)) %>%
mutate(player_performance = performance$player_performance )%>%
mutate(drive = ifelse(player_dist_ride==0, "no", "yes") %>% as.factor()) %>%
mutate(player_kills_d = ifelse(player_kills==0, "no", "yes") %>% as.factor()) A manipulação acima cria as seguintes variáveis:
player_distcomo o log da soma deplayer_dist_rideeplayer_dist_walkplayer_assists_dcomo uma dummy: 1 se o jogador deu assistência; 0 c.c.player_performaeccomo a combinação deplayer_dmg,player_assistseplayer_killsdrivecomo uma dummy: 1 se o jogador dirigiu; 0 c.c.player_kills_dcomo uma dummy: 1 se jogador matou alguém; 0 c.c.
Vejamos como ocorre a distribuição das variáveis numéricas após as transformações:
g1 <-
pubg_tpp1 %>%
# select_if(~ !length(table(.x))==2 & is.numeric(.x)) %>% colnames() %>%
select(player_survive_time,player_performance,player_dist) %>% colnames() %>%
map2(c("Densidade", "", ""),
~ plot_grid(
pubg_tpp1 %>%
ggplot(aes_string(x=.x)) +
geom_histogram(aes(y=..density..),colour="black", fill="white", bins = 15) +
geom_density(alpha=.2, fill="lightgrey") +
scale_x_continuous()+
ggtitle(.x)+
labs(x="", y=.y)+
theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank())
,
pubg_tpp1 %>%
ggplot(aes_string(, y=.x))+
geom_boxplot(aes(x=" "))+
labs(x="", y="")+
coord_flip()+
theme(axis.title.x=element_blank(),
axis.text.x=element_blank(),
axis.ticks.x=element_blank()),
ncol = 1, nrow = 2, align = "v", rel_heights = c(3,1)
)
)
dat <-
pubg_tpp1 %>%
select_if(~.x %>% table %>% length == 2) %>%
mutate_at(2,~if_else(.x==0, "no", "yes")) %>%
.[,-1]
g2 <- map2(colnames(dat),
c( "Porcentagem", "",""),
~ dat[,.x] %>%
tidyr::gather() %>%
group_by(key, value) %>%
summarise(n = n()) %>%
mutate(prop = n/sum(n)) %>%
ggplot(aes(x = key, y = prop,fill = value)) +
geom_bar(position = "fill",stat = "identity", alpha=0.7) +
scale_y_continuous(labels = percent_format())+
labs(x="", y = .y)+
scale_fill_manual(values = c("grey", "#FCC14B"), name = "Legenda:")
)
grid.arrange(g1[[1]], g1[[2]], g1[[3]],g2[[1]], g2[[2]], g2[[3]], ncol=3, heights=c(3/5, 2/5))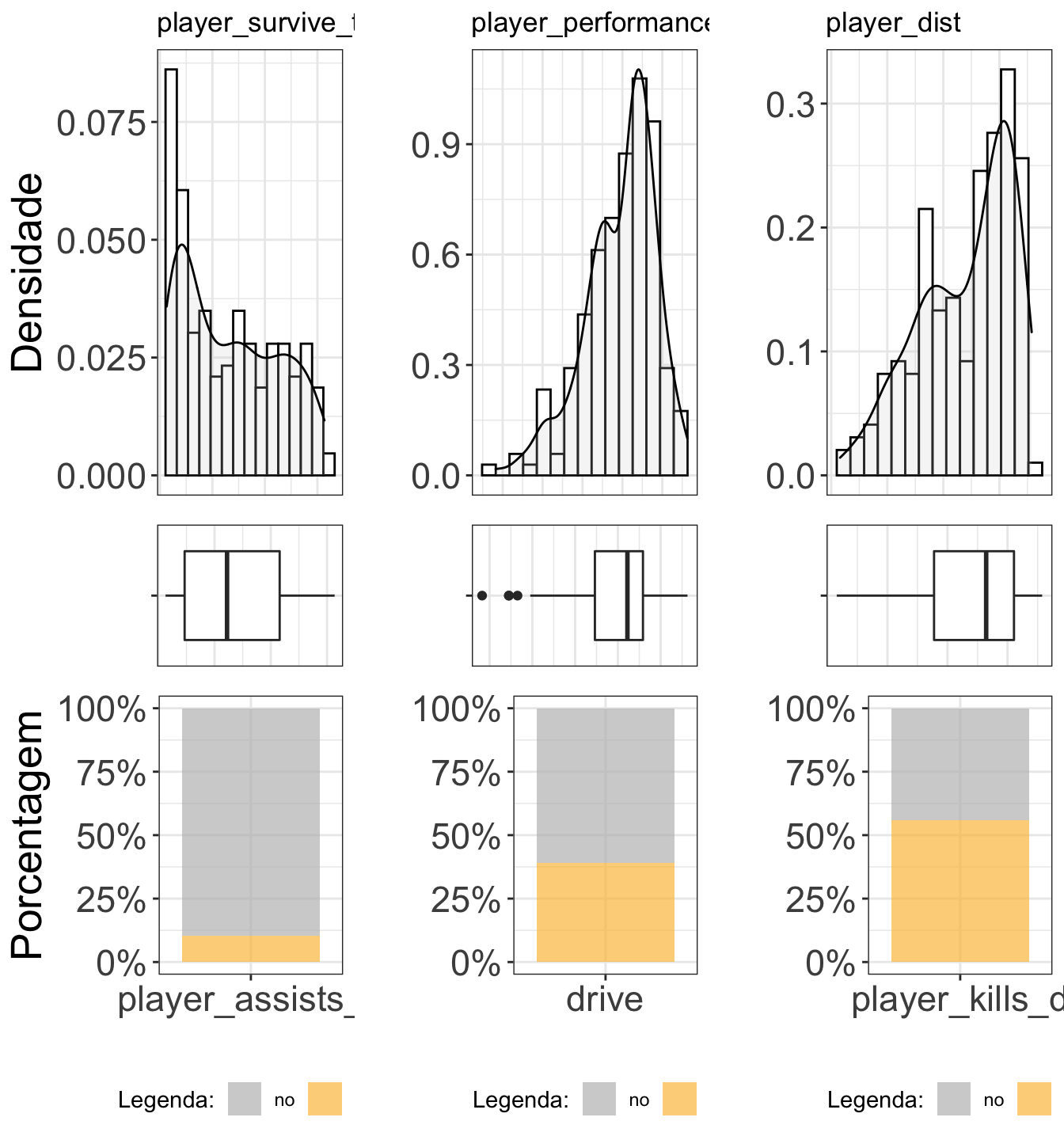
Apos a transformação a distribuição e demais informações dos dados, vejamos novamente a distribuição das variáveis da amostra com os gráficos de dispersão, densidade e correlações levando em conta se dirigiu ou não:
grafico_descritivo(x = pubg_tpp1,
colNames = c('player_survive_time', "player_performance", 'player_dist',
'player_assists_d',"player_kills_d", 'drive'),
color='drive',
colors = c("grey", "#FCC14B"))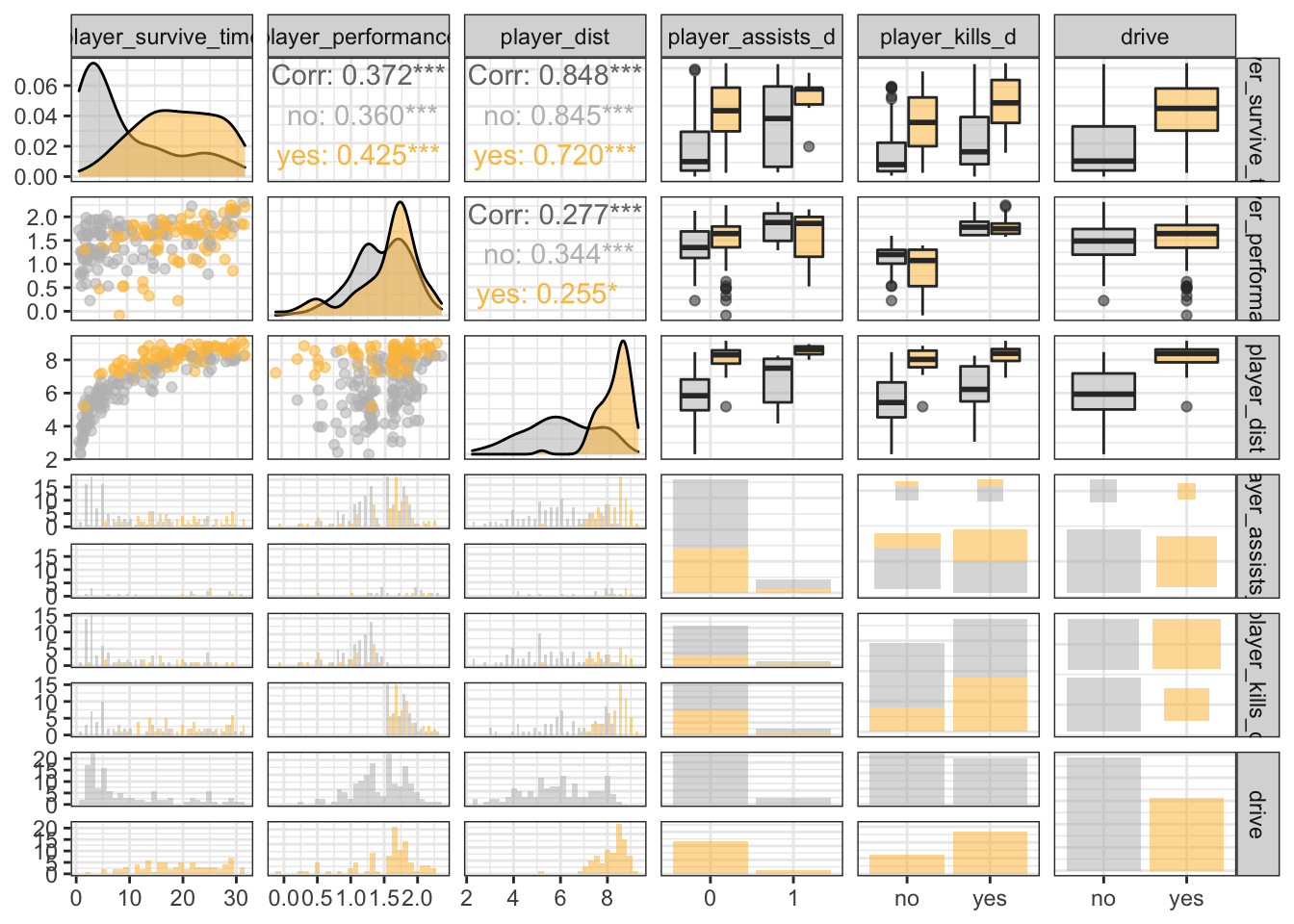
O fato do jogador ter dirigido ou não exibiu padrões interessantes, pode ser que seja significante no ajuste do modelo final.
Análise de sobrevivencia
O passo inicial de qualquer análise estatística consiste em uma descrição dos dados e o principal componente da análise descritiva envolvendo dados de tempo de vida é a função de sobrevivência: \(S(t) = P(T>t)\), que determina a probabilidade de um indivíduo sobreviver por mais do que um determinado tempo \(t\), ou por no mínimo um tempo igual a \(t\).
A descrição dos dados já foi realizada, agora faremos a descrição envolvendo a função de sobrevivência.
Kaplan-Meier
Para isso existem algumas alternativas como o estimador de Kaplan-Meier, que utiliza os conceitos de independência e de probabilidade condicional para deduzir a probabilidade de sobreviver até o tempo \(t\).
Veja a seguir são ajustados os modelos univariados de Kaplan-Meier para cada uma das coivaráveis da amostra:
surv <- Surv(pubg_tpp1$player_survive_time)
resultado_km <-
list(geral = survfit(surv ~ 1 ,data = pubg_tpp1),
player_assists_d = survfit(surv ~ player_assists_d ,data = pubg_tpp1),
drive = survfit(surv ~ drive,data = pubg_tpp1 ),
player_kills_d = survfit(surv ~ player_kills_d,data = pubg_tpp1))Veja os resultados da função de sobrevivência sem levar em consideração nenhuma das coivaráveis:
surv_summary(resultado_km[[1]], pubg_tpp1) %>% .[1:5,-ncol(.)] %>% cbind(variable = "Geral") %>%
select(variable, everything())%>%
kable2()A função surv_summary() retorna um quadro de dados com as seguintes colunas:
- time: o tempo em que a curva tem um passo.
- n.risk: o número de sujeitos em risco em t.
- n.evento: o número de eventos que ocorrem no tempo t.
- n.censor: número de eventos censurados.
- surv: estimativa da probabilidade de sobrevivência.
- std.err: erro padrão de sobrevivência.
- superior: extremidade superior do intervalo de confiança
- inferior: extremidade inferior do intervalo de confiança
- estratos: indica a estratificação da estimativa de curvas. Os níveis de estratos (um fator) são os rótulos das curvas (se houver).
Log-rank
Além da análise visual das estimativas é importante comparar as curvas de sobrevivência com testes de hipóteses para obter-se significância estatística para nossas afirmações.
O teste log rank é um teste não paramétrico, que não faz suposições sobre as distribuições de sobrevivência. Essencialmente, o teste log rank compara o número observado de eventos em cada grupo com o que seria esperado se a hipótese nula fosse verdadeira. Considere então \(H_0: S_1(t)=S_2(t)\) para todo \(t\) no período de acompanhamento (ou seja, se as curvas de sobrevivência fossem idênticas). A estatística utilizada no teste é um \(T\) com distribuição aproximadamente \(\chi^2\) com 1 grau de liberdade.
O objeto criado abaixo guarda o valor p para o teste de log-rank de cada em cada um dos modelos:
resultado_log_rank <-
c(geral = "",
player_assists_d=round(1-pchisq(survdiff(surv~player_assists_d,data = pubg_tpp1)$chisq,1),5),
drive=round(1-pchisq(survdiff(surv~drive,data=pubg_tpp1)$chisq,1),5),
player_kills_d=round(1-pchisq(survdiff(surv~player_kills_d,data=pubg_tpp1)$chisq,1),5)
)Os gráficos gerados a partir dos modelos ajustados acima bem como o resultado dos testes de log-rank são exibidos na imagem a seguir:
survplot <- map2(resultado_km,
case_when(resultado_log_rank == '0' ~ "log-rank: \n p < 0,00001",
resultado_log_rank == "" ~ "log-rank não se aplica",
resultado_log_rank != '0' | resultado_log_rank != '' ~
paste0("log-rank: \n p =",as.numeric(resultado_log_rank))),
~ autoplot(.x)+
ggtitle(stringr::str_remove_all(names(.x$strata)[1],"(=no|=yes)"))+
annotate("label",y = 0.20, x = 5,
label = .y,
size = 4, colour = "red",hjust=0.1)+
scale_fill_manual(values = c("grey", "#FCC14B"))+
scale_color_manual(values = c("grey", "#FCC14B"))+
theme(legend.position = c(0.85,0.7))+
scale_x_continuous(limits = c(0,30), breaks = seq(0,30,5))
)
grid.arrange(survplot[[1]], survplot[[2]] ,survplot[[3]], survplot[[4]], ncol=2)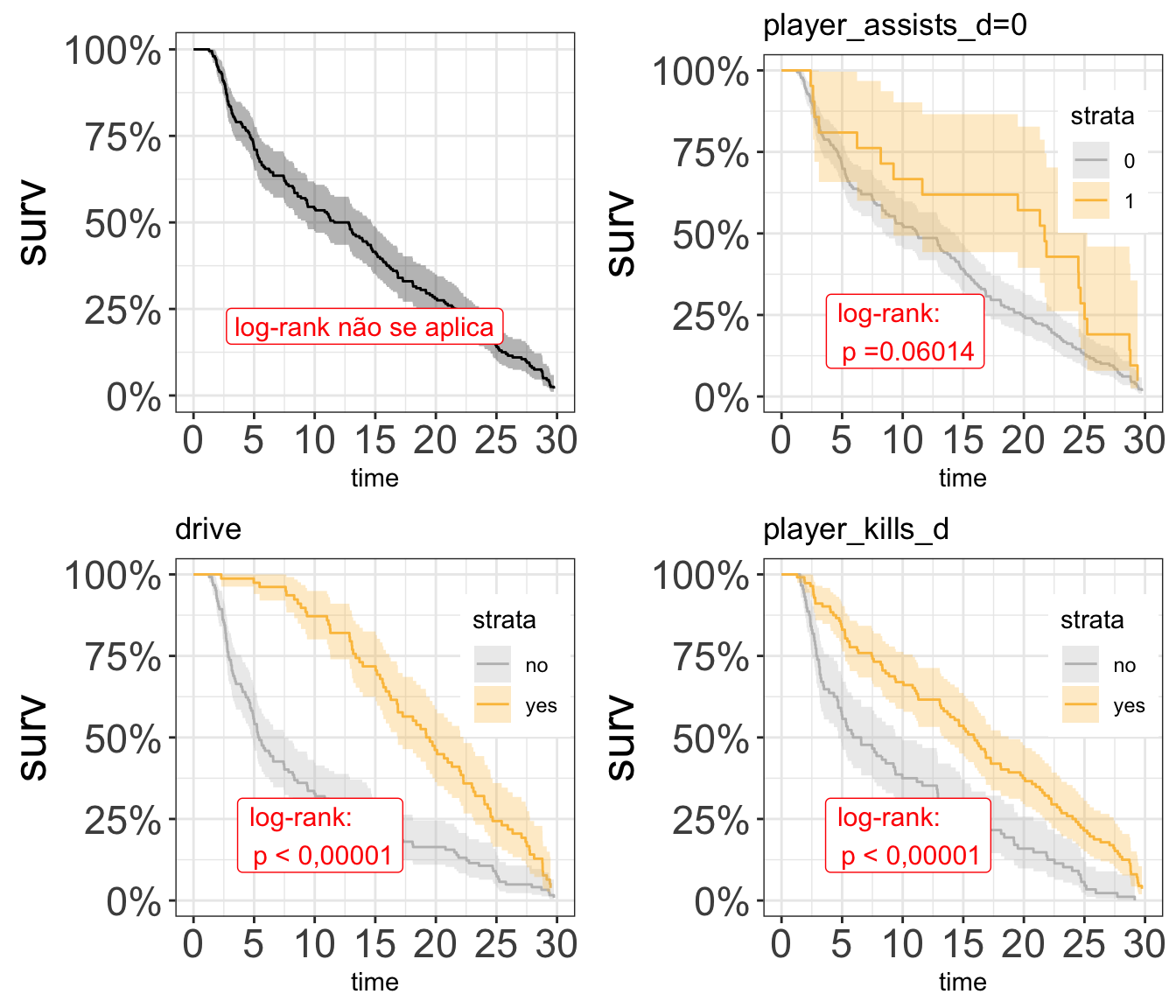
O eixo horizontal (eixo x) representa o tempo em minutos, e o eixo vertical (eixo y) mostra a probabilidade de sobrevivência ou a proporção de jogadores que sobrevivem. As linhas representam curvas de sobrevivência dos dois grupos.
Uma queda vertical nas curvas indica um evento. No tempo zero, a probabilidade de sobrevivência é de 1,0 (ou 100% dos jogadores vivos).
Interpretação: Pelo gráfico, aparentemente não existe diferença no tempo de sobrevivência com estratificação dos dados de acordo com quem deu assistência ou não, já para o teste que compara igualdade de funções de sobrevivência das demais variáveis, existem evidencias estatísticas para rejeitar a hipótese de que não há diferença na sobrevida entre os dois grupos
Função de risco (hazard) ou taxa de falha
Função de risco (hazard) ou taxa de falha é o risco “instantâneo” denotada por \(\lambda(t)\) é uma taxa, não uma probabilidade e pode assumir qualquer valor real maior que zero.
No exemplo representa a taxa de incidência ou risco acumulado para um indivíduo morrer até o momento \(t\), dado que sobreviveu até este momento. É muito informativa quando comparada com a função de sobrevivência pois diferentes \(S(t)\) podem ter formas semelhantes, enquanto que respectivas \(\lambda(t)\) podem diferir drasticamente.
survplot <-
map(resultado_km ,
~ ggsurvplot(.x, conf.int = TRUE,
palette = c("grey", "#FCC14B"),
risk.table = F,break.time.by = 5,
fun = "cumhaz",title = stringr::str_remove_all(names(.x$strata)[1],"(=no|=yes)"))
)
arrange_ggsurvplots(survplot, print = TRUE,
ncol = 2, nrow = 2)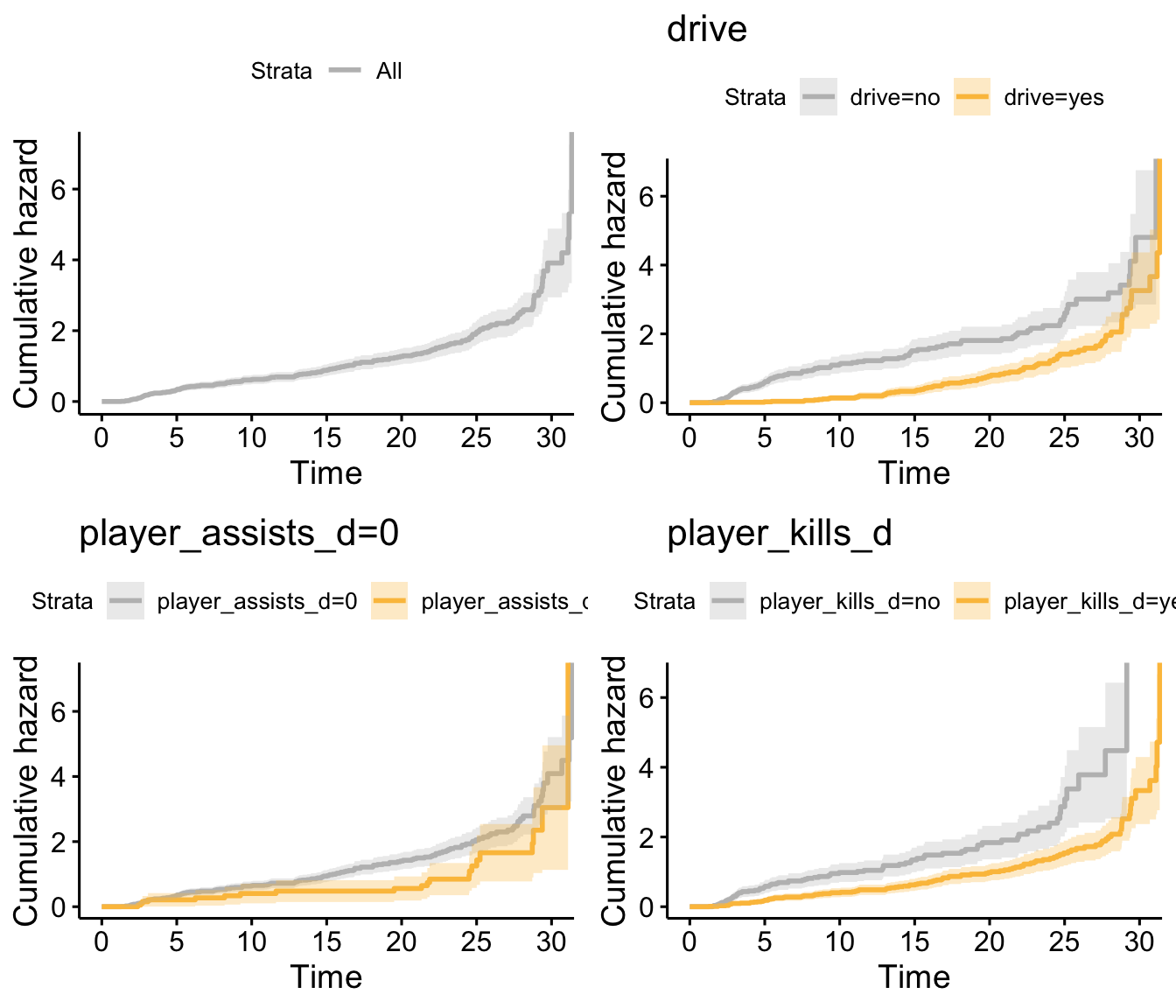
O risco cumulativo \(H( t)\) pode ser interpretado como a força cumulativa da mortalidade. Em outras palavras, corresponde ao número de eventos que seriam esperados para cada indivíduo pelo tempo t se o evento fosse um processo repetitivo.
Modelo de cox
É caracterizado pela presença dos coeficientes \(\beta\)s que medem os efeitos (semelhantes à análise de regressão logística múltipla e linear múltipla) das variáveis explicativas sobre a função de risco. Em um modelo de regressão de riscos proporcionais de Cox, a medida do efeito é a taxa de risco, que é o risco de falha, dado que o participante sobreviveu até um tempo específico.
Algumas das suposições para o correto uso do modelo de regressão de riscos proporcionais de Co incluem:
- independência dos tempos de sobrevivência entre indivíduos distintos na amostra,
- relação multiplicativa entre os preditores e o risco,
- uma taxa de risco constante ao longo do tempo.
O modelo de riscos proporcionais de Cox é chamado de modelo semi-paramétrico , porque não há suposições sobre o formato da função de risco de linha de base. No entanto, existem outras suposições, como observado acima.
É possível utilizar as estatísticas de Wald, da razão de verossimilhança e escore para fazer inferências sobre os parâmetros do modelo
Veja a seguir a significância dos coeficiente estimado em modelos univariados para cada variável candidata ao modelo:
# Modelos univariados
covariates <- c("player_kills","player_dist_ride","player_performance",
"player_dist_walk","player_dmg", "player_dist",
"player_assists_d","drive", "player_kills_d")
univ_formulas <- map(covariates,~ as.formula(paste('Surv(player_survive_time) ~', .x)))
univ_models <- map( univ_formulas, ~coxph(.x, data = pubg_tpp1))
# estrair resultados
map2_df(univ_models,
covariates,
function(x,y){
x = summary(x)
p.value = signif(x$wald["pvalue"], digits=2)
wald.test = signif(x$wald["test"], digits=2)
beta = signif(x$coef[1], digits=2);#coeficient beta
HR = signif(x$coef[2], digits=2);#exp(beta)
HR.confint.lower = signif(x$conf.int[,"lower .95"], 2)
HR.confint.upper = signif(x$conf.int[,"upper .95"],2)
HR = paste0(HR, " (", HR.confint.lower, "-", HR.confint.upper, ")")
res = tibble(y,beta, HR, wald.test, p.value)
colnames(res) = c("covariates","beta", "HR (95% CI for HR)", "wald.test", "p.value")
res
}) %>%
kable2(linhas = 7)Modelo de Cox usando uma variável categórica retorna uma razão de risco, que, acima de 1 indica uma covariável que está positivamente associada à probabilidade do evento e, portanto, negativamente associada ao tempo de sobrevida. O oposto vale para HR menor que um e HR = 1 indica que a covariável não tem efeito.
final_model <-
coxph(Surv(player_survive_time) ~ player_performance+player_dist+drive,
data = pubg_tpp1,x=T,method="breslow")
summary(final_model)## Call:
## coxph(formula = Surv(player_survive_time) ~ player_performance +
## player_dist + drive, data = pubg_tpp1, x = T, method = "breslow")
##
## n= 200, number of events= 200
##
## coef exp(coef) se(coef) z Pr(>|z|)
## player_performance -0.7469 0.4738 0.1787 -4.179 2.92e-05 ***
## player_dist -1.7599 0.1721 0.1150 -15.307 < 2e-16 ***
## driveyes 0.8832 2.4186 0.2091 4.225 2.39e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## exp(coef) exp(-coef) lower .95 upper .95
## player_performance 0.4738 2.1105 0.3338 0.6726
## player_dist 0.1721 5.8117 0.1374 0.2156
## driveyes 2.4186 0.4135 1.6055 3.6434
##
## Concordance= 0.883 (se = 0.008 )
## Likelihood ratio test= 362.7 on 3 df, p=<2e-16
## Wald test = 274 on 3 df, p=<2e-16
## Score (logrank) test = 407.8 on 3 df, p=<2e-16No modelo ajustado note-se que existe uma associação negativa entre player_performance e mortalidade e entre player_dist e mortalidade (ou seja, o risco de morte diminui para jogadores que percorrem maiores distâncias e possuem melhor performance).
As estimativas dos parâmetros representam o aumento no log esperado do risco relativo para cada aumento de uma unidade no preditor, mantendo os outros preditores constantes.
Para interpretabilidade, calcularemos as taxas de risco exponenciando das estimativas dos parâmetros. Para a player_performance, \(exp(-0.7469196)= 0.4738239\). Isso implica que diminui para \(47.38\) do valor original do risco esperado em relação a um aumento de uma unidade na performance, mantendo as demais variáveis constantes. A interpretação de player_dist em escala logarítimica é feita de maneira semelhante.`
Já para os jogadores onde drive = 1 (que dirigiram durante a partida) existe uma relação positiva, como \(exp(0.8831835)= 2.4185871\). O risco esperado corresponde à \(2.4185871\) do valor original nos que dirigiram em comparação aos que não dirigiram, mantendo as demais variáveis constantes.
map2_df(1:3,final_model$coefficients %>% names(),~
tibble(
variable = .y,
beta = signif(summary(final_model)$coef[.x,1], digits=2), #coeficient beta
HR = signif(summary(final_model)$coef[.x,2], digits=2), #exp(beta)
HR.confint.lower = signif(summary(final_model)$conf.int[.x,"lower .95"], 2),
HR.confint.upper = signif(summary(final_model)$conf.int[.x,"upper .95"],2)) %>%
mutate(HR= paste0(HR, " (", HR.confint.lower, "-", HR.confint.upper, ")")
)
) %>% kable2()Em suma:
- HR = 1: sem efeito
- HR <1: Redução do risco
- HR> 1: aumento do risco
Resíduos de Martingal e Deviance
Como foi visto, o modelo de regressão de riscos proporcionais de Cox faz diversas suposições que precisam ser conferidas após o ajuste do modelo para chegar a qualidade de seus resultados pois um modelo mais ajustado pode trazer resultados enganosos e que não façam sentido algum
Gráficos dos resíduos Martingal ou deviance contra os tempos fornecem uma forma de verificar a adequação do modelo ajustado, bem como ajudar na detecção de observações atípicas.
Deviance
Esses resíduos, que são uma tentativa de tornar os resíduos Martingal mais simétricos em torno do zero, facilitam, em geral, a detecção de pontos atípicos (outliers). Se o modelo for apropriado, esses resíduos devem apresentar um comportamento aleatório em torno de zero.
Martingal
Esses resíduos são vistos como uma estimativa do numero de falhas em excesso observada nos dados mas não predito pelo modelo. Os mesmos são usados, em geral, para examinar a melhor forma funcional (linear, quadrática, etc.) para uma dada covariavel em um modelo de regressão assumido para os dados do estudo.
res <-
tibble(residuo_deviance = resid(final_model,type="deviance") ,
residuo_martingal = resid(final_model,type="martingal"),
linear_predictors = final_model$linear.predictors)
# Graficos:
grid.arrange(
ggplot(res, aes(x=linear_predictors, y=residuo_martingal))+ geom_point()+geom_hline(yintercept=0, color='coral')+ylab("Resíduos Martingual"),
ggplot(res, aes(x=linear_predictors, y=residuo_deviance))+ geom_point()+geom_hline(yintercept=0, color='coral')+ylab("Deviance"),
ncol=2
)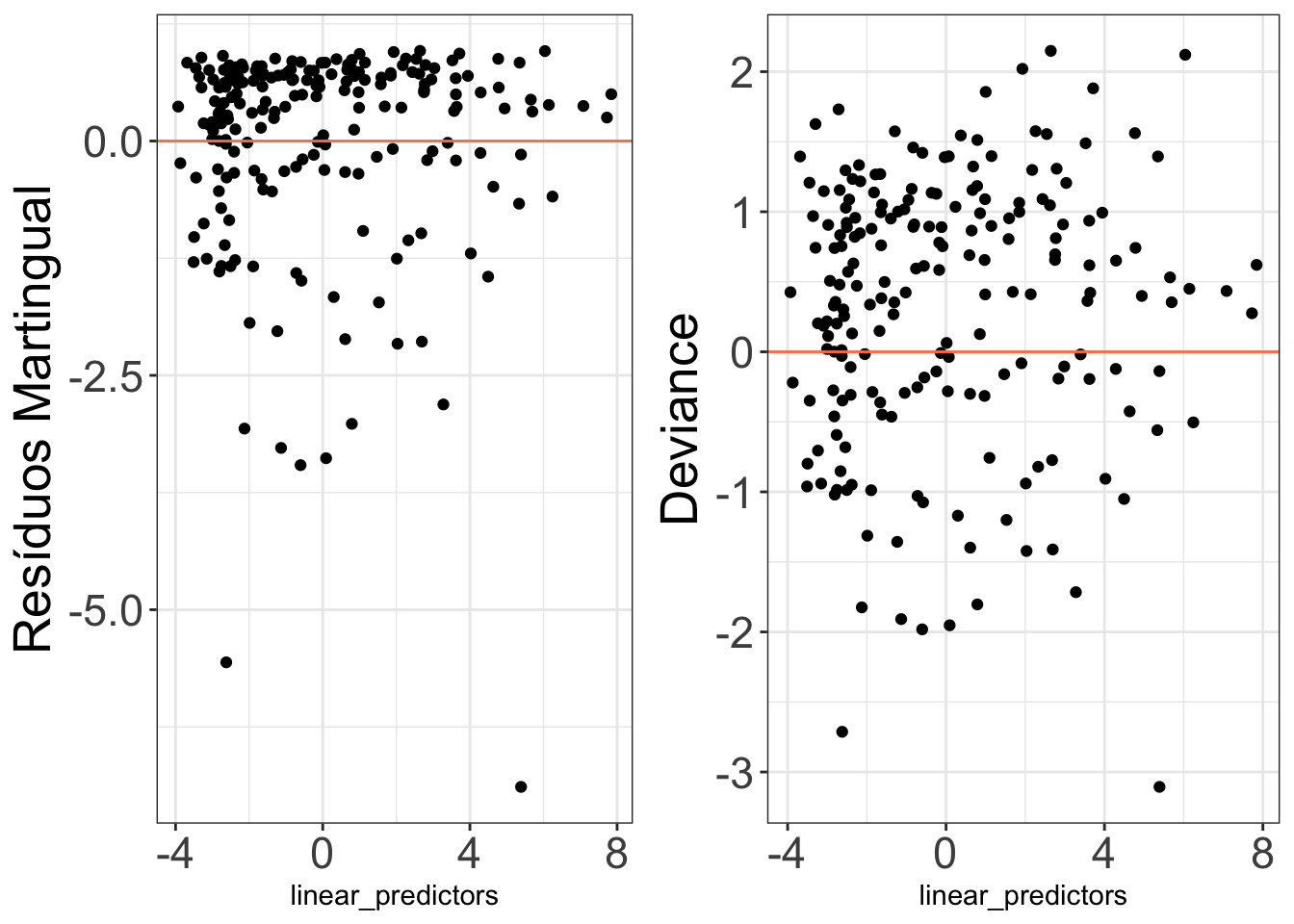
Interpretação:
- Martingal: Parecido com deviance mais acentuado;
- Deviance: Modelo não eh tao ruim assim, se fosse um modelo linear talvez deveríamos tomar cuidado.
Residuos de Schoenfeld
Em princípio, os resíduos de Schoenfeld são independentes do tempo. Um gráfico que mostra um padrão não aleatório contra o tempo é evidência de violação da suposição de hipótese.
Para testar a suposição de riscos proporcionais:
final_model %>% cox.zph %>% ggcoxzph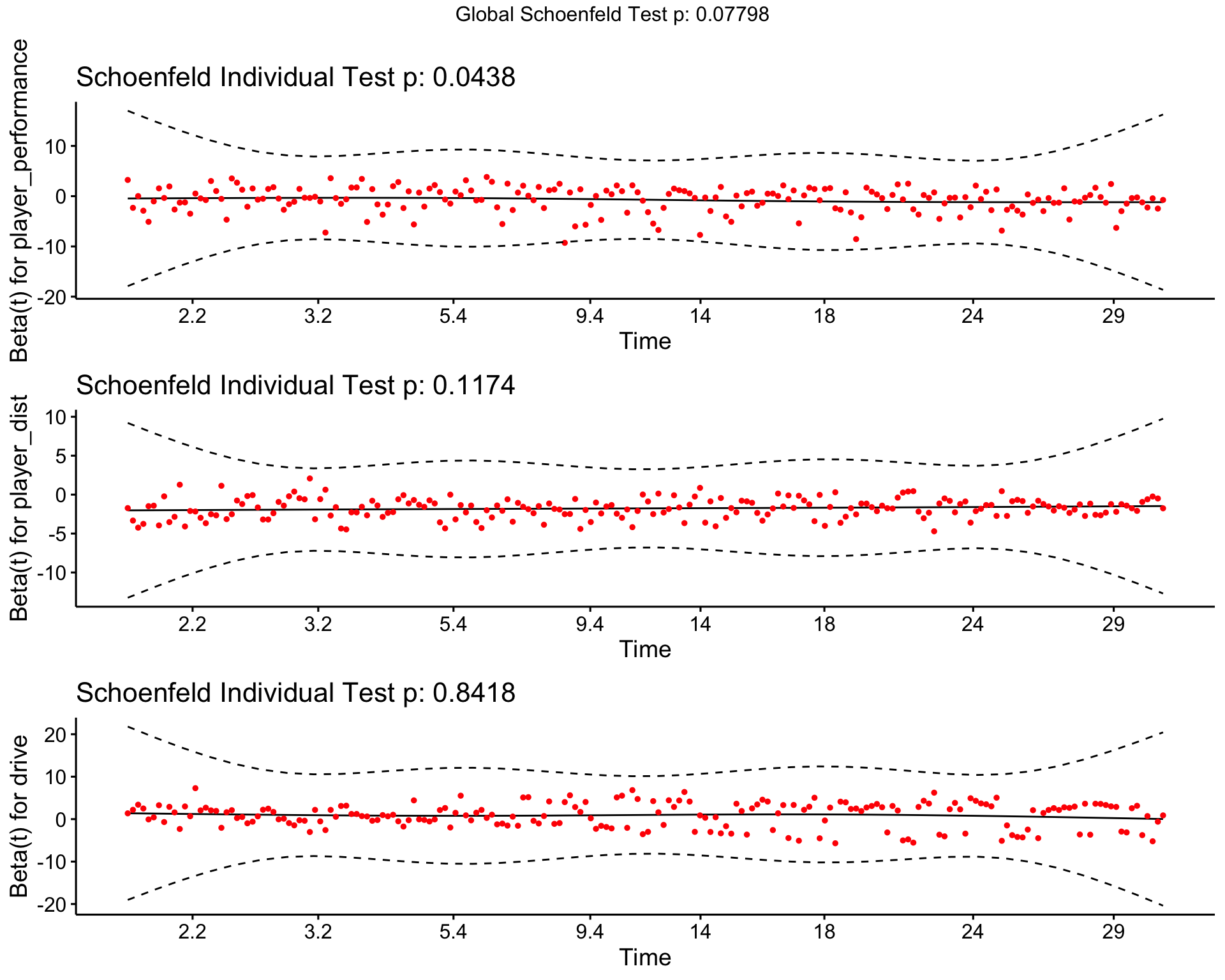
A partir da inspeção gráfica, não há padrão com o tempo. A suposição de riscos proporcionais parece ser suportada pelas covariáveis
Considerações finais
Como era de se esperar, o risco de ser abatido diminui para jogadores que possuem melhor performance e também para os jogadores que percorrem maiores distâncias (o que mostra que ficar parado no jogo em uma zona pode não ser a melhor ideia, já é quanto mais se movimenta maior a quantidade de itens que podem ser coletados).
Interessante notar que a curva de sobrevivência para os jogadores que dirigiram apresenta resultado oposto ao risco esperado nos que dirigiram, isso ocorre pois esses dois modelos calculam medidas diferentes.
Referências
- Carvalho,M.A., Andreozzi,V.L., Codec¸o,C.T., Campos,D.P., Barbosa,M.T.S., Shimakura,S.E., Análise de sobrevivência: Teoria e aplicações em saúde, Segunda Edição, Editora FIOCRUZ, Rio de Janeiro, 2011.
- Colosimo,E.A., Giolo,S.R., Análise de sobrevivência aplicada, ABE-Projeto Fisher, São Paulo, 2010
- Lewis,E.E., Introduction to reliability engineering, John Wiley, New York, 1987
- http://sphweb.bumc.bu.edu/otlt/MPH-Modules/BS/BS704_Survival/BS704_Survival6.html
- http://www.sthda.com/english/wiki/cox-model-assumptions
Cuiriosidades / Leituras futuras:
- Evaluating Random Forests for Survival Analysis Using Prediction Error Curves: https://www.jstatsoft.org/article/view/v050i11
- randomForestSRC: https://cran.r-project.org/web/packages/randomForestSRC/index.html
- WTTE-RNN - Less hacky churn prediction: https://ragulpr.github.io/2016/12/22/WTTE-RNN-Hackless-churn-modeling/
- Weibull Time To Event Recurrent Neural Network: https://github.com/ragulpr/wtte-rnn/
- Neural Networks as Statistical Methods in Survival Analysis: https://www.stats.ox.ac.uk/pub/bdr/NNSM.pdf
- Continuous and Discrete Time Survival Analysis: Neural Network Approaches: http://pcwww.liv.ac.uk/~afgt/eleuteri_lyon07.pdf
- Cox Proportional Hazards Model - h2O Documentation: http://s3.amazonaws.com/h2o-release/h2o/master/1579/docs-website/datascience/coxph.html
- Introduction to H2OCoxPH: https://www.slideshare.net/0xdata/introduction-to-h2ocoxph






























Share this post
Twitter
LinkedIn
Email