Um estudo sobre modelos de aprendizagem baseados em árvores com desafio do Kaggle
Um estudo aplicado de modelos de aprendizagem baseados em árvores utilizando a base de dados do Kaggle para prever o preço final de casas residenciais em Ames, Iowa, utilizando uma variedade de aspectos

Kaggle
Segundo o Wikipédia: “Kaggle é a maior comunidade mundial de cientistas de dados e machine learning.” Aprendo muito estudando as resoluções de alguns competidores pois lá é possível conferir tanto as metodologias utilizadas pelos competidores quando os códigos e é notável o cuidado dos participantes para que seja possível a reprodutibilidade dos resultados, o que pode impulsionar o aprendizado.
O Kaggle trabalha com a ideia de gamificação, que é um assunto do qual já escrevi em um post sobre gamificação e porque aprender R é tão divertido e gosto deste conceito de se criar jogos para motivar e engajar as pessoas em atividades profissionais e a ideia de se estar em um jogo possibilita doses de motivação especialmente a quem gosta de competir.
A plataforma é focada em competições que envolvem modelagem preditiva, que julgam apenas o seu desempenho preditivo, embora a inteligibilidade não deixe de ser importante. Neste post farei também a modelagem descritiva com modelos de aprendizagem baseados em árvores, na qual o principal objetivo será obter informações sobre os dados para o ajuste dos modelos preditivos que iremos submeter à competição do Kaggle House Prices: Advanced Regression Techniques.
A diferença entre modelos preditivos e descritivos não é tão rigorosa assim pois algumas das técnicas podem ser utilizadas para ambos e geralmente um modelo pode servir para ambos os propósitos (mesmo que de de forma insuficiente).
Além dos modelos de machine learning baseados em árvores, também será ajustado um modelo de regressão linear multivariado para compararmos os resultados dos ajustes e submeter nossas previsões no site do kaggle.
Os pacotes que serão utilizados serão os seguintes:
library(purrr) # Programacao funciona
library(broom) # Arrumar outputs
library(dplyr) # Manipulacao de dados
library(magrittr) # pipes
library(funModeling) # df_status()
library(plyr) # revalue()
library(gridExtra) # Juntar ggplots
library(reshape) # funcao melt()
library(rpart) # Arvore de Decisoes
library(rpart.plot) # Plot da Arvore de Decisoes
library(data.table) # aux na manipulacao do heatmap
library(readr) # Leitura da base de dados
library(stringr) # Manipulacao de strings
library(ggplot2) # Graficos elegantes
library(caret) # Machine Learning
library(GGally) # up ggplot
library(ggfortify) # autoplot()Base de dados
A base de dados deste post vem de uma competição ótima para estudantes de ciência de dados de dados com alguma experiência com R ou Python e noções básicas de machine learning e estatística.
Pode ser útil para aqueles que desejam expandir seu conjunto de habilidades em uma tarefa de regressão, quando a variável \(y\) que desejamos estimar é do tipo numérico (contínuo ou discreto).
Trata-se do conjunto de dados Ames Housing que foi compilado por Dean De Cock para uso em educação de ciência de dados.
train <- read_csv("train.csv")
test <- read_csv("test.csv")
full <- bind_rows(train, test)
id <- test$Id
full %<>% select(-Id)Descrição da Competição
Traduzido do site oficial do kaggle:
"Peça a um comprador que descreva a casa dos seus sonhos, e eles provavelmente não começarão com a altura do teto do porão ou a proximidade de uma ferrovia leste-oeste. Mas o conjunto de dados desta competição de playground prova que muito mais influencia as negociações de preço do que o número de quartos ou uma cerca branca.
Com 79 variáveis explicativas descrevendo (quase) todos os aspectos de casas residenciais em Ames, Iowa, esta competição desafia você a prever o preço final de cada casa."
Portanto, primeiramente vamos entender o comportamento da variável resposta, depois buscar quais dessas 79 variáveis explicativas são mais importantes para representar a variação do preço de venda das casas através dos métodos baseados em árvores e por fim ajustar os modelos propostos e submeter nossas estimativas no site!
Análise exploratória dos dados
Antes de pensar em ajustar algum modelo é extremamente necessário entender como se comportam os dados, portanto, tanto a variável resposta quanto as variáveis explicativas serão avaliadas.
Variável resposta:
SalePrice - o preço de venda da propriedade em dólares. Essa é a variável de destino que estamos tentando prever.
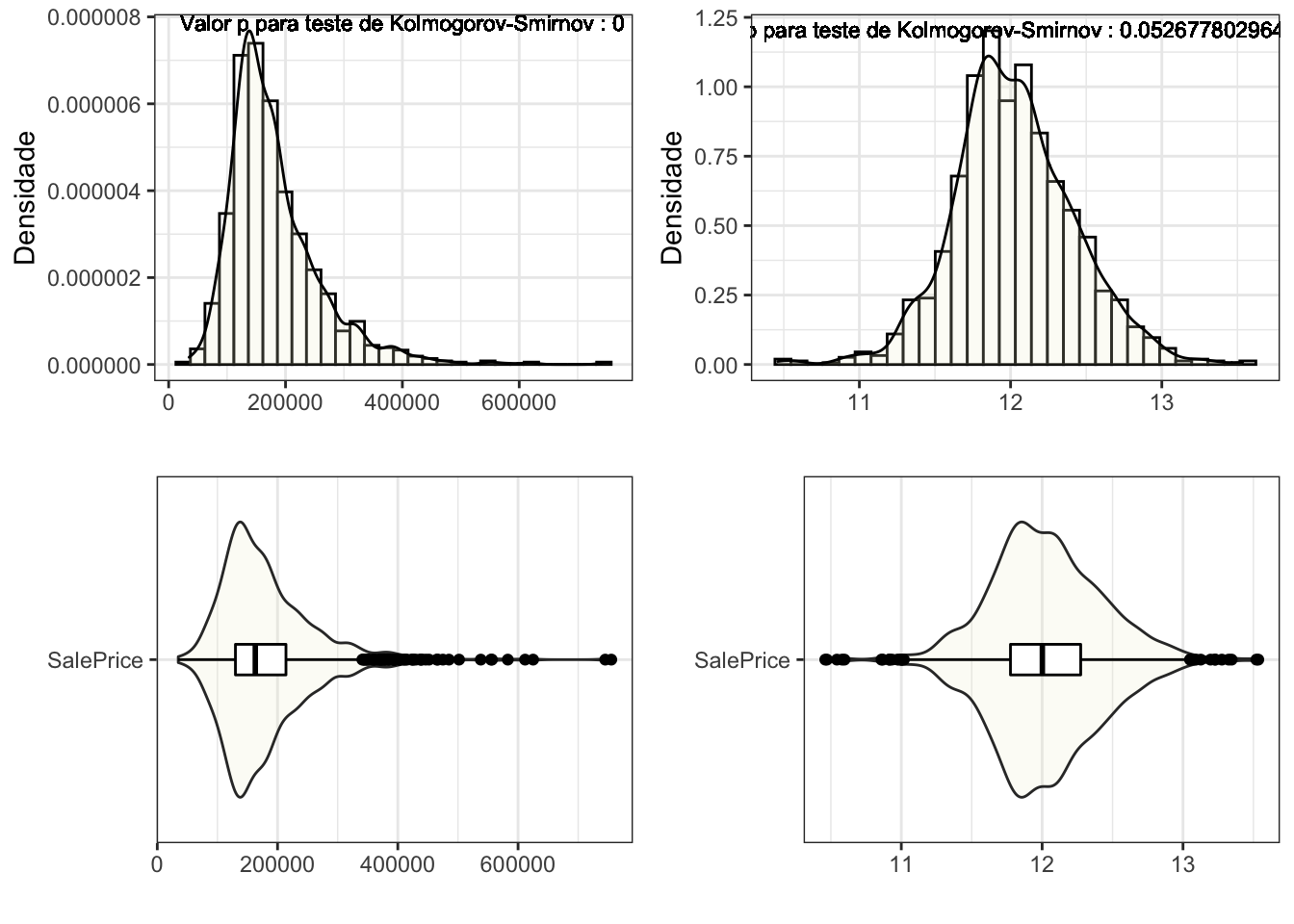
Note que a distribuição dos dados referentes ao preço de venda se distribui de maneira assimétrica e não possuem evidências de normalidade dos dados. Apesar dos métodos baseados em árvore se tratarem de técnicas não paramétricas essa transformação será feita pois ao final deste post desejo comparar os resultados com um modelo de regressão linear múltipla.
Árvore de decisão
Uma técnica muito popular que é mais comumente usada para resolver tarefas de classificação de dados porém a árvore conhecida como CART (Classification and Regression Trees)(Breiman, 1986) lida com todos os tipos de atributos (incluindo atributos numéricos que são tratados a partir da criação de intervalos). Para seu ajuste é possível realizar podas e produzir árvores binárias.
A construção da árvore é realizada por meio do algoritmo que iterativamente analisa os atributos descritivos de um conjunto de dados previamente rotulado. Sua popularidade como apoio para a tomada de decisão se deve principalmente ao fato da fácil visualização do conhecimento gerado e o fácil entendimento.
Outra característica legal da árvore de decisões é que ela permite ajustar um modelo sem um pré-processamento detalhado, pois é fácil de ajustar, aceita valores faltantes e é de fácil interpretação, veja:
library(rpart)
control <- rpart.control(minsplit =10, # o número mínimo de observações em um nó
cp = 0.006 # parametro de complexidade q controla o tamanho da arvore
)
rpartFit <- rpart(exp(SalePrice) ~ . , train, method = "anova", control = control)
rpart.plot::rpart.plot(rpartFit,cex = 0.6)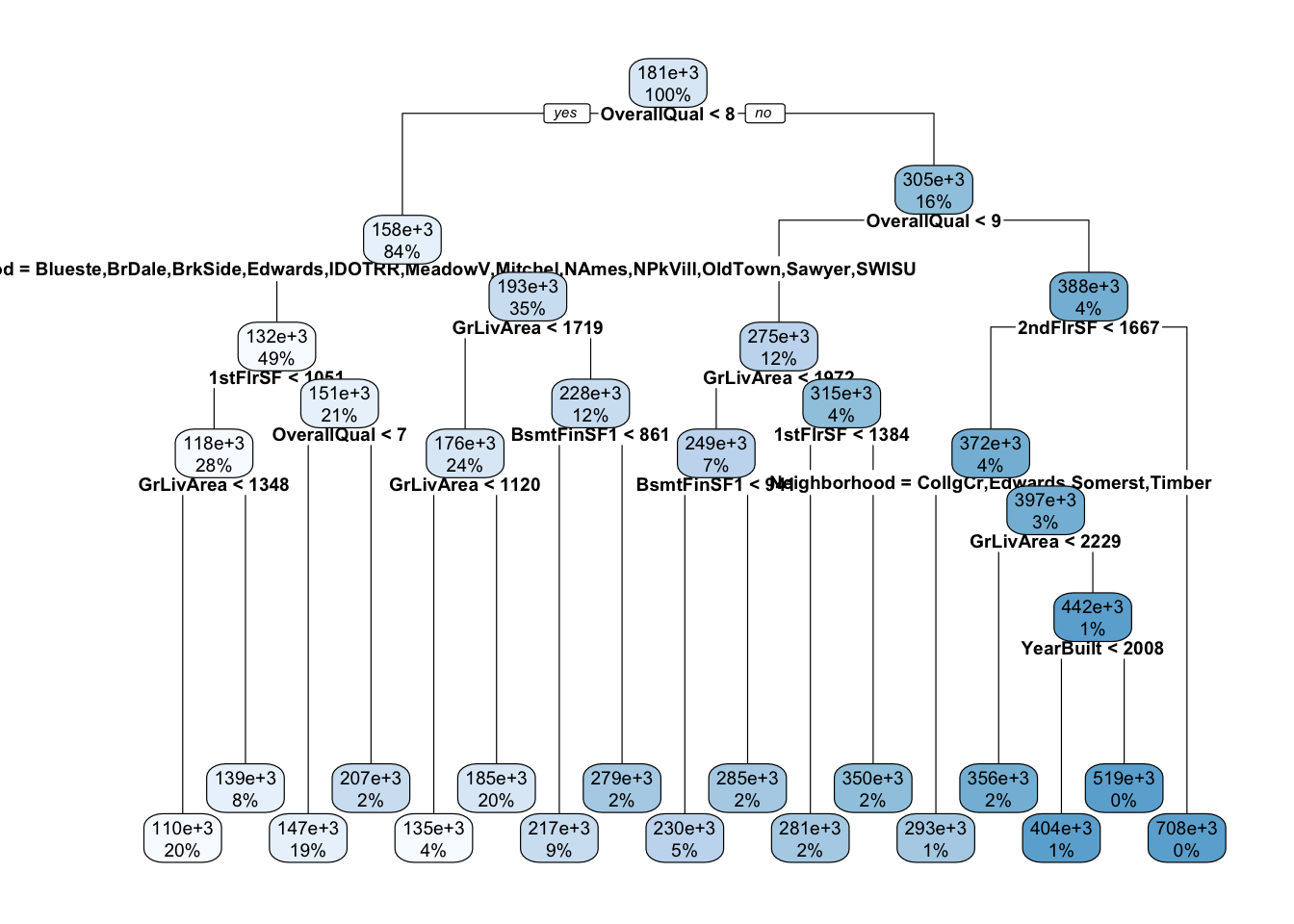
No topo, vemos o primeiro nó com 100% das observações, que representa o total da base (100%). Em seguida, vemos que a primeira variável que determina o preço de venda das casas SalePrice é a variável OverallQual. As casas que apresentaram OverallQual < 7.5 ocorrem em maior proporção do que as que tiveram OverallQual>7.5. A interpretação pode continuar dessa forma recursivamente.
É possível notar que as variáveis OverallQual,Neighborhood,1stFlrSF,2ndFlrSF,GrLivArea, BsmtFinSF1 foram as que melhor representaram os dados de acordo com os parâmetros que determinamos para ajustar esta árvore, vejamos com mais detalhes se existe relação linear e intensidade e direção dessa relação com o coeficiente de correlação de Pearson entre estas variáveis dois a dois e em relação à variável resposta:
devtools::source_url("https://raw.githubusercontent.com/gomesfellipe/functions/master/correlations_for_ggpairs.R")
train %>%
select(SalePrice,OverallQual,`1stFlrSF`,`2ndFlrSF`,GrLivArea,BsmtFinSF1) %>%
ggpairs(lower = list(continuous = my_fn))+
theme_bw()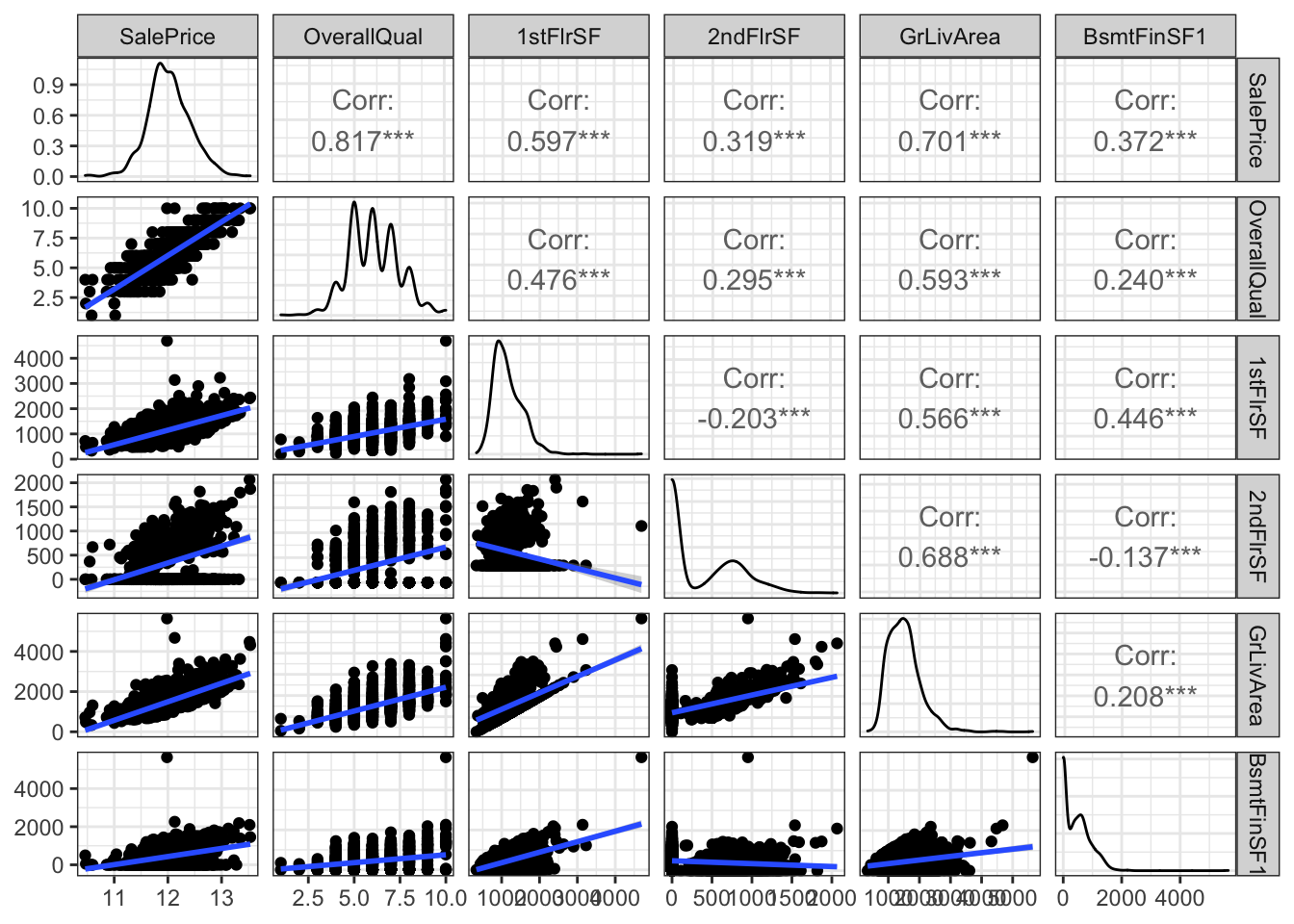
Com esta figura temos muitas informações, destaca-se que todas essas variáveis possuem algum tipo de relação linear com a variável resposta, a menor correlação observada foi com o BsmtFinSF1 e a variável que apresentou a maior correlação foi a OverallQual. Atenção para a correlação entre SalePrice e OverallQual, pois Overallqual parece ser uma variável ordinal e uma outra medida de correlação que melhor representaria esta relação é o coeficiente de correlação de Spearman, veja:
cor(full$SalePrice, full$OverallQual, method = "spearman", use = "complete.obs")## [1] 0.8098286Um pouco diferente do resultado da correlação de Pearson pois avalia relações lineares, já a correlação de Spearman avalia relações monótonas, sejam elas lineares ou não.
Análise exploratória e input de NAs
Arrumar a base de dados é uma tarefa longa e que geralmente consome grande parte no tempo em um projeto de ciência de dados. Não adianta usar o algorítimo mais poderoso de machine learning se a base de dados não estiver arrumada de maneira que possibilite a análise dos dados.
Para obter informações da amostra, confira no link do dataset da competição no Kaggle. Na página é possível conferir a descrição da amostra e nela nota-se que alguns dos valores faltantes possuem significado, então é necessário rotulá-los para que o R possa interpretar estes valores da maneira correta.
Status da amostra
Conferindo o status da amostra com a função df_status() do pacote funModeling:
full %>%
df_status(print_results = F) %>%
as_tibble() %>%
arrange(-p_na, -p_zeros)## # A tibble: 80 x 9
## variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
## <chr> <int> <dbl> <int> <dbl> <int> <dbl> <chr> <int>
## 1 PoolQC 0 0 2909 99.7 0 0 character 3
## 2 MiscFeature 0 0 2814 96.4 0 0 character 4
## 3 Alley 0 0 2721 93.2 0 0 character 2
## 4 Fence 0 0 2348 80.4 0 0 character 4
## 5 SalePrice 0 0 1459 50.0 0 0 numeric 663
## 6 FireplaceQu 0 0 1420 48.6 0 0 character 5
## 7 LotFrontage 0 0 486 16.6 0 0 numeric 128
## 8 GarageYrBlt 0 0 159 5.45 0 0 numeric 103
## 9 GarageFinish 0 0 159 5.45 0 0 character 3
## 10 GarageQual 0 0 159 5.45 0 0 character 5
## # … with 70 more rowsNote que as variáveis problemáticas foram ordenadas de forma decrescente (maior número de dados faltantes e zeros) vamos tratar uma de cada vez partindo da variável mais crítica
Pool
PoolQCé a variável que possui maisNAe a descrição da base informa que:
PoolQC: qualidade da piscina
- Ex Excelente
- Gd Good
- TA Média / Típica
- Fa Pequena
- NA sem piscina
É possível observar que se trata de uma variável ordinal, portanto vamos criar uma variável auxiliar (pois esta descrição se repete em outras variáveis):
# Criando variável auxilar ordinal
Qualidade <- c('None' = 0, 'Po' = 1, 'Fa' = 2, 'TA' = 3, 'Gd' = 4, 'Ex' = 5)
full %<>%
mutate(PoolQC = ifelse(PoolQC %>% is.na, "None", PoolQC) %>% as.factor() ) %>%
mutate(PoolQC = as.integer(revalue(PoolQC, Qualidade)))Além disso, existe outra variável relacionada à piscina, veja:
full %>%
select(names(full)[names(full) %>% str_detect("Pool")]) %>%
table ## PoolQC
## PoolArea 1 2 3 4
## 0 0 0 0 2906
## 144 1 0 0 0
## 228 1 0 0 0
## 368 0 0 0 1
## 444 0 0 0 1
## 480 0 0 1 0
## 512 1 0 0 0
## 519 0 1 0 0
## 555 1 0 0 0
## 561 0 0 0 1
## 576 0 0 1 0
## 648 0 1 0 0
## 738 0 0 1 0
## 800 0 0 1 0full %>%
select(names(full)[names(full) %>% str_detect("Pool")]) %>%
map(~sum(is.na(.x)))## $PoolArea
## [1] 0
##
## $PoolQC
## [1] 0# Arrumando inconsistëncias:
full %<>%
mutate(PoolQC = ifelse(PoolQC == 0 & PoolArea !=0, 2, PoolQC))
# Arrumando inconsistëncias:
full %<>%
mutate(Pool = ifelse(PoolQC == 0 & PoolArea ==0, "no", "yes"))Misc
Se referem aos recursos diversos
full %>%
select(names(full)[names(full) %>% str_detect("Misc")],
SalePrice
) %>%
map(~sum(is.na(.x)))## $MiscFeature
## [1] 2814
##
## $MiscVal
## [1] 0
##
## $SalePrice
## [1] 1459MiscFeature: recurso diverso não coberto em outras categorias
- Elevador elev
- Gar2 2nd Garage (se não for descrito na seção de garagem)
- Othr Outro
- Galpão derramado (mais de 100 SF)
- TenC Campo de ténis
- NA Nenhum
Desta vez não se trata de uma variável ordinal, vejamos:
full %<>%
mutate(MiscFeature = if_else(MiscFeature %>% is.na, "None", MiscFeature) %>% as.factor)
# Breve resumo:
g1 <-
full %>%
select(names(full)[names(full) %>% str_detect("Misc")], SalePrice) %>%
ggplot(aes(y=MiscVal,x= reorder(MiscFeature, -MiscVal,FUN = median) ,fill=MiscFeature))+
geom_boxplot()+
theme_bw() +
scale_fill_viridis_d() +
labs(x = "Recurso Diverso")
g2 <-
full %>%
select(names(full)[names(full) %>% str_detect("Misc")], SalePrice) %>%
ggplot(aes(y=SalePrice,x= reorder(MiscFeature, -MiscVal,FUN = median) ,fill=MiscFeature))+
geom_boxplot()+
theme_bw() +
scale_fill_viridis_d() +
labs(x = "Preço de Venda")
grid.arrange(g1, g2)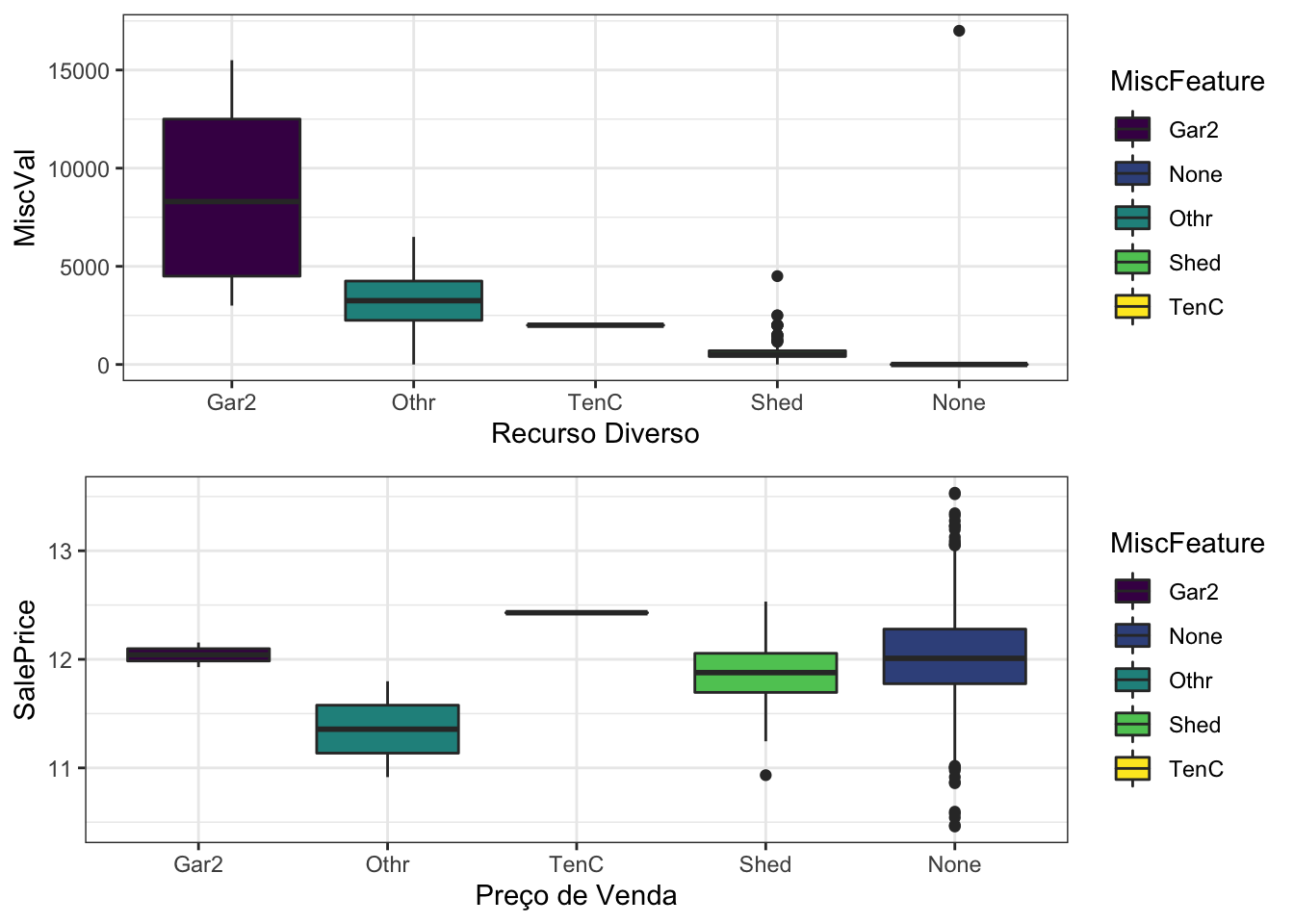
rm(g1,g2)Além disso, MiscVal: Valor do recurso variado
Alley
Alley: Tipo de acesso ao beco para a propriedade
- Grvl Cascalho
- Pave pavimentado
- NA Nenhum acesso de beco
Basta realizar o input:
full %<>%
mutate(Alley = Alley %>% str_replace_na("None")) %>%
mutate(Alley = as.factor(Alley))full[!is.na(full$SalePrice),] %>%
select(Alley, SalePrice) %>%
ggplot(aes(y=SalePrice,x= reorder(Alley, -SalePrice,FUN = median) ,fill=Alley))+
geom_boxplot()+
theme_bw() +
scale_fill_viridis_d() +
labs(x = "tipo de Acesso")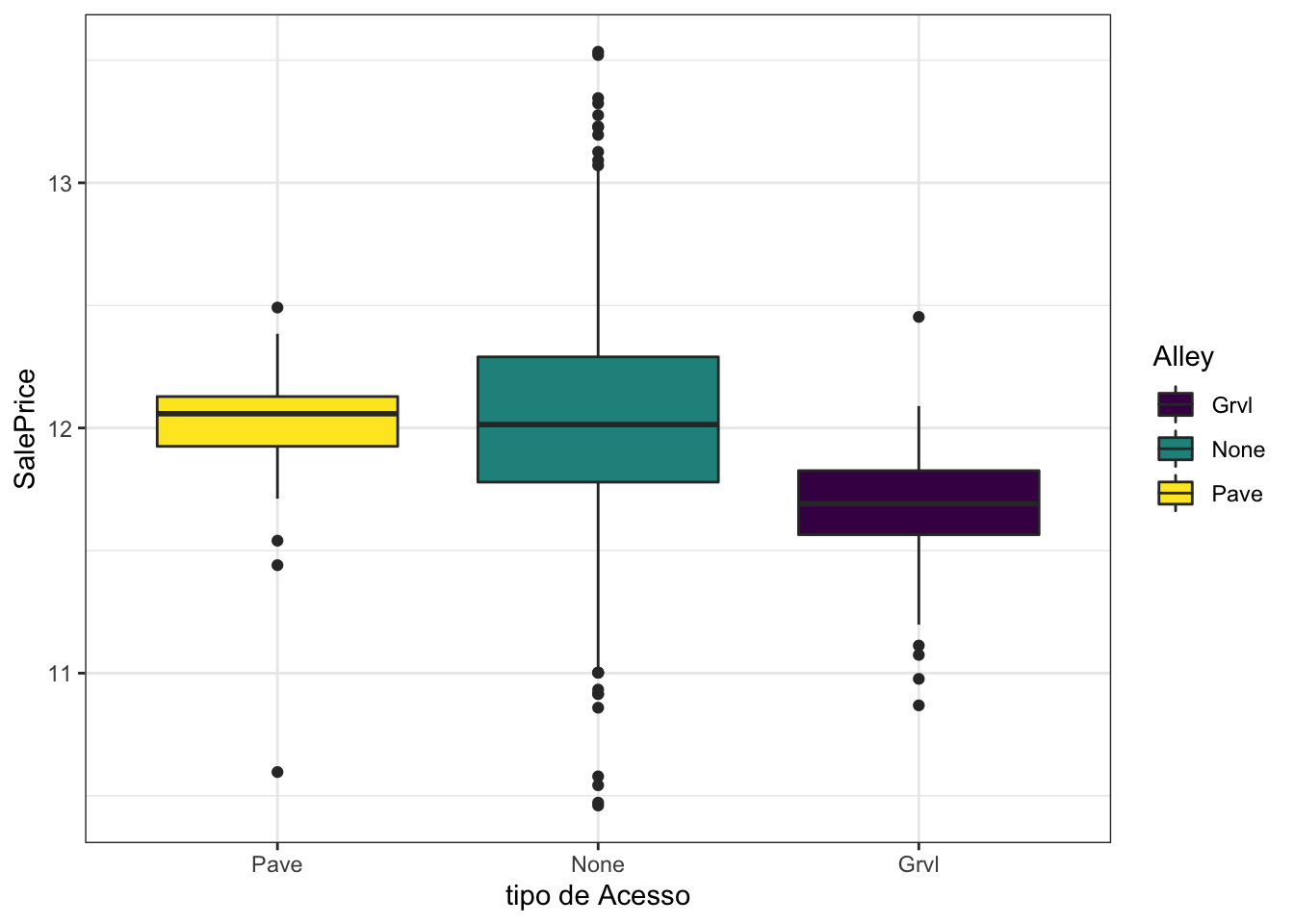
Fence
Fence: qualidade da cerca
- GdPrv Boa privacidade
- MnPrv minima privacidade
- GdWo boa madeira
- MnWw Mínima Madeira / Fio
- NA Sem cerca
Input será da seguinte forma:
full %<>%
mutate(Fence = Fence %>% str_replace_na("None"))full[1:nrow(train),] %>%
select(Fence, SalePrice) %>%
ggplot(aes(y=SalePrice,x= reorder(Fence, -SalePrice, median) ,fill=Fence))+
geom_boxplot()+
theme_bw() +
scale_fill_viridis_d() +
labs(x = "tipo de Acesso")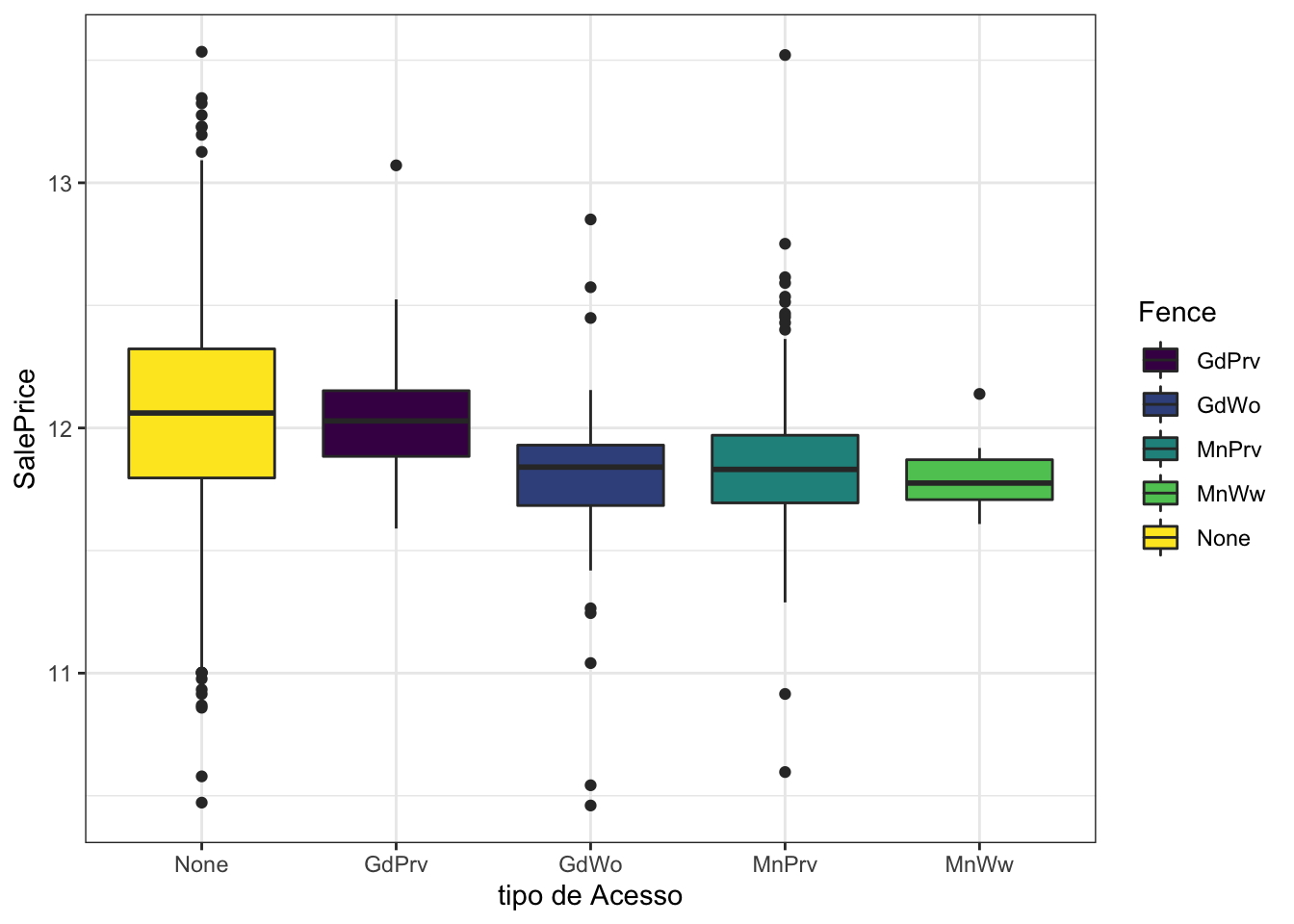
full %<>% mutate(Fence = as.factor(Fence))Aparentemente não parece existir uma relação ordinal sobre o tipo de cerca quanto ao pre;o de venda da casa, portanto foi convertida para fator
FirePlace
Variáveis relacionadas com lareira. Segundo a descrição, temos:
full %>%
select(names(full)[names(full) %>% str_detect("Fireplace")], SalePrice)## # A tibble: 2,919 x 3
## Fireplaces FireplaceQu SalePrice
## <dbl> <chr> <dbl>
## 1 0 <NA> 12.2
## 2 1 TA 12.1
## 3 1 TA 12.3
## 4 1 Gd 11.8
## 5 1 TA 12.4
## 6 0 <NA> 11.9
## 7 1 Gd 12.6
## 8 2 TA 12.2
## 9 2 TA 11.8
## 10 2 TA 11.7
## # … with 2,909 more rowsFireplaces: Numero de lareiras
FireplaceQu: Qualidade da lareira
- Ex Excellente - Excepcional Lareira de Alvenaria
- Gd Boa - Lareira de alvenaria no nível principal
- TA Média - lareira pré-fabricada na sala principal ou Lareira de alvenaria no porão
- Fa Pequena - Lareira pré-fabricada no porão
- Po Pobre - Fogão Ben Franklin
- NA sem lareira
Nota-se que se trata de uma variável ordinal de acordo com a qualidade, portanto:
full %<>%
mutate(FireplaceQu = if_else(FireplaceQu %>% is.na, "None", FireplaceQu) ) %>%
mutate(FireplaceQu = as.integer(revalue(FireplaceQu, Qualidade)))Conferindo se existem inconsistências:
full %>%
select(names(full)[names(full) %>% str_detect("Fireplace")]) %>%
table ## FireplaceQu
## Fireplaces 0 1 2 3 4 5
## 0 1420 0 0 0 0 0
## 1 0 46 63 495 627 37
## 2 0 0 10 92 112 5
## 3 0 0 1 4 5 1
## 4 0 0 0 1 0 0Lot
full %>%
select(names(full)[names(full) %>% str_detect("Lot")], SalePrice) %>%
map_dbl(~sum(is.na(.x)))## LotFrontage LotArea LotShape LotConfig SalePrice
## 486 0 0 0 1459Segundo a descrição:
LotFrontage: Ruas linearmente conectadas à propriedade
LotArea : Tamanho do lote em pés quadrados
LotShape: forma geral da propriedade
- Regue Regular
- IR1 ligeiramente irregular
- IR2 moderadamente irregular
- IR3 Irregular
LotConfig: configuração de lote
- Inside Lote muito para dentro
- Corner Canto de esquina
- CulDSac Cul-de-sac
- FR2 Frente em 2 lados da propriedade
- FR3 Frente em 3 lados da propriedade
Input para o LotFrontage será feito considerando a configuração do lote, veja:
inputsLot <- full %>%
select(LotFrontage, LotConfig) %>%
group_by(LotConfig) %>%
dplyr::summarise(Media = mean(LotFrontage, na.rm = T),
Mediana = median(LotFrontage, na.rm = T))
full$LotFrontage[is.na(full$LotFrontage) & full$LotConfig == inputsLot$LotConfig[1]] <- inputsLot$Mediana[1]
full$LotFrontage[is.na(full$LotFrontage) & full$LotConfig == inputsLot$LotConfig[2]] <- inputsLot$Mediana[2]
full$LotFrontage[is.na(full$LotFrontage) & full$LotConfig == inputsLot$LotConfig[3]] <- inputsLot$Mediana[3]
full$LotFrontage[is.na(full$LotFrontage) & full$LotConfig == inputsLot$LotConfig[4]] <- inputsLot$Mediana[4]
full$LotFrontage[is.na(full$LotFrontage) & full$LotConfig == inputsLot$LotConfig[5]] <- inputsLot$Mediana[5] Arrumando variáveis nominais e ordinais:
full %<>%
mutate(LotShape = as.integer(revalue(full$LotShape, c('IR3'=0, 'IR2'=1, 'IR1'=2, 'Reg'=3))))Garages
Variáveis relacionadas, segundo a descrição, temos:
full %>%
select(names(full)[names(full) %>% str_detect("Garage")], SalePrice) %>%
map_dbl(~sum(is.na(.x)))## GarageType GarageYrBlt GarageFinish GarageCars GarageArea GarageQual
## 157 159 159 1 1 159
## GarageCond SalePrice
## 159 1459GarageType: localização da garagem
- 2Types Mais de um tipo de garagem
- Attchd anexa a casa
- Basement tipo porao
- BuiltIn (garagem parte da casa - normalmente tem sala acima da garagem)
- CarPort Porta do carro
- Detchd nao anexa a casa
- NA Sem Garagem
GarageYrBlt: garagem do ano foi construída
GarageFinish: acabamento interior da garagem
- Fin Finished
- RFn Áspero Finalizado
- Unf inacabado
- NA Sem Garagem
GarageCars: Tamanho da garagem na capacidade do carro
GarageArea: Tamanho da garagem em pés quadrados
GarageQual: GarageQuality
- Ex Excelente
- Gd Good
- TA Típico / Médio
- FA Justo
- Po Poor
- NA Sem Garagem
GarageCond: condição de garagem
- Ex Excelente
- Gd Good
- TA Típico / Médio
- Fa Justo
- Po Poor
- NA Sem Garagem
full %<>%
mutate(GarageType = if_else(GarageType %>% is.na, "None", GarageType) ) %>%
mutate(GarageYrBlt = if_else(GarageYrBlt %>% is.na,YearBuilt, GarageYrBlt) ) %>%
mutate(GarageFinish = if_else(GarageFinish %>% is.na, "None", GarageFinish) ) %>%
mutate(GarageFinish = as.integer(revalue(GarageFinish, c('None'=0, 'Unf'=1, 'RFn'=2, 'Fin'=3)))) %>%
mutate(GarageCars = ifelse(GarageCars %>% is.na, 0, GarageCars) ) %>%
mutate(GarageArea = ifelse(GarageArea %>% is.na, 0, GarageArea)) %>%
mutate(GarageQual = if_else(GarageQual %>% is.na, "None", GarageQual)) %>%
mutate(GarageQual = as.integer(revalue(GarageQual, Qualidade))) %>%
mutate(GarageCond = if_else(GarageCond %>% is.na, "None", GarageCond)) %>%
mutate(GarageCond = as.integer(revalue(GarageCond, Qualidade)))
table(full$GarageCond)##
## 0 1 2 3 4 5
## 159 14 74 2654 15 3Bsmt
full %>%
select(names(full)[names(full) %>% str_detect("Bsmt")], SalePrice) %>%
map_dbl(~sum(is.na(.x)))## BsmtQual BsmtCond BsmtExposure BsmtFinType1 BsmtFinSF1 BsmtFinType2
## 81 82 82 79 1 80
## BsmtFinSF2 BsmtUnfSF TotalBsmtSF BsmtFullBath BsmtHalfBath SalePrice
## 1 1 1 2 2 1459BsmtQual: Avalia a altura do porão
- Ex Excelente (100+ polegadas)
- Gd Bom (90-99 polegadas)
- TA Típica (80-89 polegadas)
- Fa Justo (70-79 polegadas)
- Po Pobre (<70 polegadas
- NA Sem Porão
BsmtCond: Avalia o estado geral do porão
- Ex Excelente
- Gd Bom
- TA Típica - umidade ligeira permitida
- Fa Razoável - umidade ou alguma rachadura ou sedimentação
- Po Insuficiente - Craqueamento severo, sedimentação ou umidade
- NA Sem Porão
BsmtExposure: Refere-se a paralisações ou paredes no nível do jardim
- Gd Good Exposição
- Av Média Exposição (níveis divididos ou foyers normalmente pontuação média ou acima)
- Mn Exposição Mínima
- No Não Exposição
- NA Sem porão
BsmtFinType1: Avaliação da área acabada do porão
- GLQ Bons Viver
- ALQ Média Living Quarters
- BLQ Abaixo da média Living Quarters
- Rec Média Rec Room
- LwQ Baixa Qualidade
- Unf unfinshed
- NA nenhum porão
BsmtFinSF1: pes quadrados do tipo 1 terminado
BsmtFinType2: Avaliação do porão área terminado (se vários tipos)
- GLQ Bons aposentos
- ALQ Medianos
- BLQ abaixo da media
- Rec Aposentos média qualidade
- LwQ Baixa Qualidade
- Unf
- Não Sem Porão
BsmtFinSF2: Pés quadrados acabados do Tipo 2
BsmtUnfSF: Pés quadrados inacabados da área do porão
TotalBsmtSF: Total pés quadrados da área do porão
Input das variáveis não numéricas com None e convertendo para ordinal as variáveis com relação de ordem. Para os faltantes das variáveis numéricas foram imputados o valor 0 (zeros).
# Categóricos:
full[,names(full)[names(full) %>% str_detect("Bsmt")]] <-
full[,names(full)[names(full) %>% str_detect("Bsmt")]] %>%
select(names(full)[names(full) %>% str_detect("Bsmt")]) %>%
mutate_if( ~ !is.numeric(.x) , ~ ifelse(is.na(.x), "None", .x)) %>%
mutate(BsmtQual = as.integer(revalue(BsmtQual, Qualidade))) %>%
mutate(BsmtCond = as.integer(revalue(BsmtCond, Qualidade))) %>%
mutate(BsmtExposure = as.integer(revalue(BsmtExposure, c('None'=0, 'No'=1, 'Mn'=2, 'Av'=3, 'Gd'=4)))) %>%
mutate(BsmtFinType1 = as.integer(revalue(BsmtFinType1,c('None'=0, 'Unf'=1, 'LwQ'=2, 'Rec'=3, 'BLQ'=4, 'ALQ'=5, 'GLQ'=6))))
# Numéricos:
full[,names(full)[names(full) %>% str_detect("Bsmt")]] <-
full[,names(full)[names(full) %>% str_detect("Bsmt")]] %>%
select(names(full)[names(full) %>% str_detect("Bsmt")]) %>%
mutate_if( ~ is.numeric(.x) , ~ ifelse(is.na(.x), 0, .x))MasVnr
full %>%
select(names(full)[names(full) %>% str_detect("MasVnr")], SalePrice) %>%
map_dbl(~sum(is.na(.x)))## MasVnrType MasVnrArea SalePrice
## 24 23 1459MasVnrType: Alvenaria tipo de verniz
- BrkCmn Brick Common
- BrkFace Face de tijolos
- CBlock Bloco cinza
- None Nenhum
- Stone Pedra
MasVnrArea: Área de folheado de alvenaria em pés quadrados
full %<>%
mutate(MasVnrType = if_else(is.na(MasVnrType), "None", MasVnrType)) %>%
mutate(MasVnrType = as.integer(revalue(MasVnrType, c('None'=0, 'BrkCmn'=0, 'BrkFace'=1, 'Stone'=2)))) %>%
mutate(MasVnrArea = if_else(is.na(MasVnrArea), 0, 1))Variáveis restantes com poucos NA
A estratégia adotada para imputar estes dados será tomada de maneira arbitrária. Os valores faltantes serão preenchidos com o valor comum mais frequente daquela variável. As variáveis que restam são:
full %>%
df_status(print_results = F) %>%
as_tibble() %>%
arrange(-p_na, -p_zeros)## # A tibble: 81 x 9
## variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
## <chr> <int> <dbl> <int> <dbl> <int> <dbl> <chr> <int>
## 1 SalePrice 0 0 1459 50.0 0 0 numeric 663
## 2 MSZoning 0 0 4 0.14 0 0 character 5
## 3 Utilities 0 0 2 0.07 0 0 character 2
## 4 Functional 0 0 2 0.07 0 0 character 7
## 5 Exterior1st 0 0 1 0.03 0 0 character 15
## 6 Exterior2nd 0 0 1 0.03 0 0 character 16
## 7 Electrical 0 0 1 0.03 0 0 character 5
## 8 KitchenQual 0 0 1 0.03 0 0 character 4
## 9 SaleType 0 0 1 0.03 0 0 character 9
## 10 PoolArea 2906 99.6 0 0 0 0 numeric 14
## # … with 71 more rowsVejamos:
MSZoning: Identifica a classificação geral de zoneamento da venda.
- Será convertida para fator, variável nominal
KitchenQual: Qualidade da cozinha
- Será convertida para ordinal
Utilities: Tipo de utilidade disponível
- Será removida
Functional: Funcionalidade doméstica
- Será considerada como ordinal
Exterior1st: revestimento Exterior em casa
- Convertida para fator, variável nominal
Electrical: Sistema elétrico
- Convertida para fator, variável nominal
SaleType: Tipo de venda
- Convertida para fator, variável nominal
full <- full %>%
mutate(MSZoning = ifelse(is.na(MSZoning),
full$MSZoning %>% table %>% sort %>% names %>% last, MSZoning)) %>%
mutate(MSZoning = as.factor(MSZoning)) %>%
mutate(KitchenQual = ifelse(is.na(KitchenQual),
full$KitchenQual %>%
table %>% sort %>% names %>% last, KitchenQual)) %>%
mutate(KitchenQual = as.integer(revalue(as.character(full$KitchenQual), Qualidade))) %>%
select(-Utilities) %>%
mutate(Exterior1st = ifelse(is.na(Exterior1st),
full$Exterior1st %>% table %>% sort %>% names %>% last, Exterior1st)) %>%
mutate(Exterior1st = as.factor(Exterior1st)) %>%
mutate(Exterior2nd = ifelse(is.na(Exterior2nd),
full$Exterior2nd %>% table %>% sort %>% names %>% last, Exterior2nd)) %>%
mutate(Exterior2nd = as.factor(Exterior2nd)) %>%
mutate(Electrical = ifelse(is.na(Electrical),
full$Electrical %>% table %>% sort %>% names %>% last, Electrical)) %>%
mutate(Electrical = as.factor(Electrical)) %>%
mutate(SaleType = ifelse(is.na(SaleType ),
full$SaleType %>% table %>% sort %>% names %>% last, SaleType )) %>%
mutate(SaleType = as.factor(SaleType ))
full[is.na(full$Functional),"Functional"] <- full$Functional %>% table %>% sort %>% names %>% last
full$Functional = as.integer(revalue(full$Functional, c('Sal'=0, 'Sev'=1, 'Maj2'=2, 'Maj1'=3, 'Mod'=4, 'Min2'=5, 'Min1'=6, 'Typ'=7)))
full[is.na(full$KitchenQual),"KitchenQual"] <- full$KitchenQual %>% table %>% sort %>% names %>% last %>% as.numeric()
full$KitchenQual = as.integer(revalue(as.character(full$KitchenQual), Qualidade))
# full[is.na(full$Electrical),"Electrical"] <- 3
to_remove <- full %>% map(~table(.x) %>% length()) %>% .[.== 1] %>% names()
full <- full %>% select(-one_of(to_remove))Status da base no momento:
full %>%
df_status(print_results = F) %>%
as_tibble() %>%
arrange(-p_na,-p_zeros, type)## # A tibble: 79 x 9
## variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
## <chr> <int> <dbl> <int> <dbl> <int> <dbl> <chr> <int>
## 1 SalePrice 0 0 1459 50.0 0 0 numeric 663
## 2 PoolArea 2906 99.6 0 0 0 0 numeric 14
## 3 3SsnPorch 2882 98.7 0 0 0 0 numeric 31
## 4 LowQualFinSF 2879 98.6 0 0 0 0 numeric 36
## 5 MiscVal 2816 96.5 0 0 0 0 numeric 38
## 6 BsmtHalfBath 2744 94 0 0 0 0 numeric 3
## 7 ScreenPorch 2663 91.2 0 0 0 0 numeric 121
## 8 BsmtFinSF2 2572 88.1 0 0 0 0 numeric 272
## 9 EnclosedPorch 2460 84.3 0 0 0 0 numeric 183
## 10 HalfBath 1834 62.8 0 0 0 0 numeric 3
## # … with 69 more rowsTransformando o character para factor:
full %<>% mutate_if(is.character, as.factor)Transformando novamente nossa base de treino e de teste:
train <- full[1:nrow(train),] %>% as.data.frame()
test <- full[(nrow(train)+1):nrow(full),] %>% select(-SalePrice) %>% as.data.frame()
# # Input Missing
# train_miss_model = preProcess(train, "knnImpute")
# train = predict(train_miss_model, train)
# test = predict(train_miss_model, test)
#
# train$SalePrice <- yMachine Learning com algorítmos de aprendizagem baseados em árvores
Os métodos baseados em árvores fornecem modelos preditivos de alta precisão, estabilidade e facilidade de interpretação. Ao contrário dos modelos lineares, eles são capazes de lidar bem com relações não-lineares além de poderem ser adaptados para resolver tanto problemas de classificação quanto problemas de regressão.
Algoritmos como árvores de decisão, random forest e “gradient boosting” estão sendo muito usados em todos os tipos de problemas de data science e é notável o uso desses algorítimos para resolver os desafios do Kaggle. Para resolver este problema utilizaremos estes três algoritmos e ao final, pegando carona na seleção de variáveis para os algoritmos de árvore, será ajustado um modelo de regressão linear para compararmos e conferirmos a significância estatística de cada uma das variáveis.
VarImp com Random Forest
Um dos benefícios da floresta aleatória é o poder de lidar com grande conjunto de dados com maior dimensionalidade e identificar as variáveis a importância das variáveis, que pode ser uma característica muito útil porém deve ser feita com cautela.
Veja uma reflexão (traduzida) da nota de Leo Breiman (Universidade da Califórnia em Berkeley)
“Uma nota filosófica: RF é um exemplo de uma ferramenta que é útil para fazer análises de dados científicos; Mas os algoritmos mais inteligentes não substituem a inteligência humana e o conhecimento dos dados do problema; Pegue a saída de florestas aleatórias não como verdade absoluta, mas como suposições geradas por um computador inteligente que podem ser úteis para levar a uma compreensão mais profunda do problema.”
O ajuste da árvore será feito com o pacote caret e o estudo de estimativas de erro foi definido como o Out of bag que remove a necessidade de um conjunto de teste pois é o erro médio de previsão em cada amostra de treinamento \(x_i\) , usando apenas as árvores que não tinham \(x_i\) em sua amostra de bootstrap.
set.seed(1)
control <- trainControl(method = "oob",verboseIter = F)
rfFit1 <- train(SalePrice ~. ,
data=train,
method="rf",
metric = "Rsquared",
trControl = control,
preProcess = c("knnImpute")
)
randomForest::varImpPlot(rfFit1$finalModel)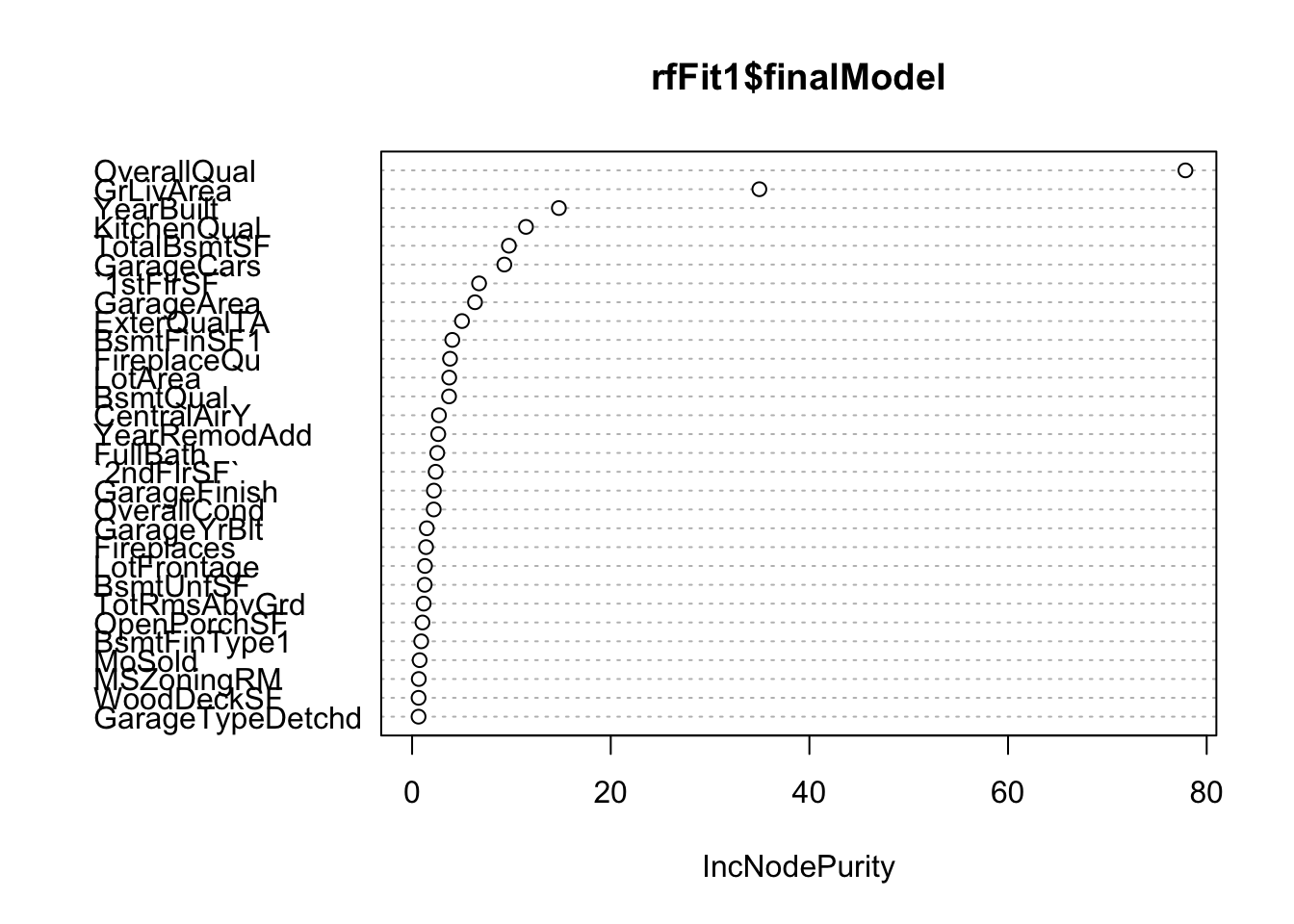
rfFit1$finalModel$importance %>%
as.data.frame %>%
mutate(row = rownames(.)) %>%
arrange(desc(IncNodePurity)) %>%
as_tibble()## # A tibble: 217 x 2
## IncNodePurity row
## <dbl> <chr>
## 1 77.9 OverallQual
## 2 35.0 GrLivArea
## 3 14.8 YearBuilt
## 4 11.5 KitchenQual
## 5 9.75 TotalBsmtSF
## 6 9.29 GarageCars
## 7 6.74 `1stFlrSF`
## 8 6.33 GarageArea
## 9 5.02 ExterQualTA
## 10 4.04 BsmtFinSF1
## # … with 207 more rowsApós inspecionar a importância das variáveis vamos selecionar as seguintes variáveis:
full %<>%
select(
SalePrice , Neighborhood, OverallQual , GrLivArea , YearBuilt , KitchenQual,
GarageCars , GarageArea , `1stFlrSF` , ExterQual , BsmtFinSF1 , FireplaceQu,
BsmtQual , `2ndFlrSF` , CentralAir , GarageFinish, YearRemodAdd, FullBath,
GarageYrBlt, Fireplaces , LotFrontage , BsmtUnfSF , TotalBsmtSF , BsmtFinType1,
OpenPorchSF, GarageType , BsmtExposure, OverallCond , TotalBsmtSF , LotArea
)Portanto, vamos definir novamente o conjunto de dados de treino e de teste:
train <- full[1:nrow(train),] %>% as.data.frame()
test <- full[(nrow(train)+1):nrow(full),-1] %>% as.data.frame()Variáveis numéricas
Após a seleção dessas variáveis, vamos entender como elas estão correlacionadas dois a dois com o coeficiente de correlação de pearson, exibindo a matrix em um Heatmap (ou mapa de calor ), que é uma representação gráfica de dados em que os valores individuais contidos em uma matriz representados como cores.
cormat <-
full %>%
select(SalePrice, everything()) %>%
select_if(is.numeric) %>%
as.data.frame() %>%
cor(use = "na.or.complete") %>%
melt
cormat %>%
ggplot( aes(reorder(Var1,value), reorder(Var2,value), fill=value))+
geom_tile(color="white")+
scale_fill_gradient2(low="blue", high="red", mid="white", midpoint=0, limit=c(-1,1), space="Lab", name="Pearson\nCorrelation")+
theme_bw()+
theme(axis.text.x=element_text(angle=45, vjust=1, size=10, hjust=1))+
coord_fixed()+
labs(x="",y="")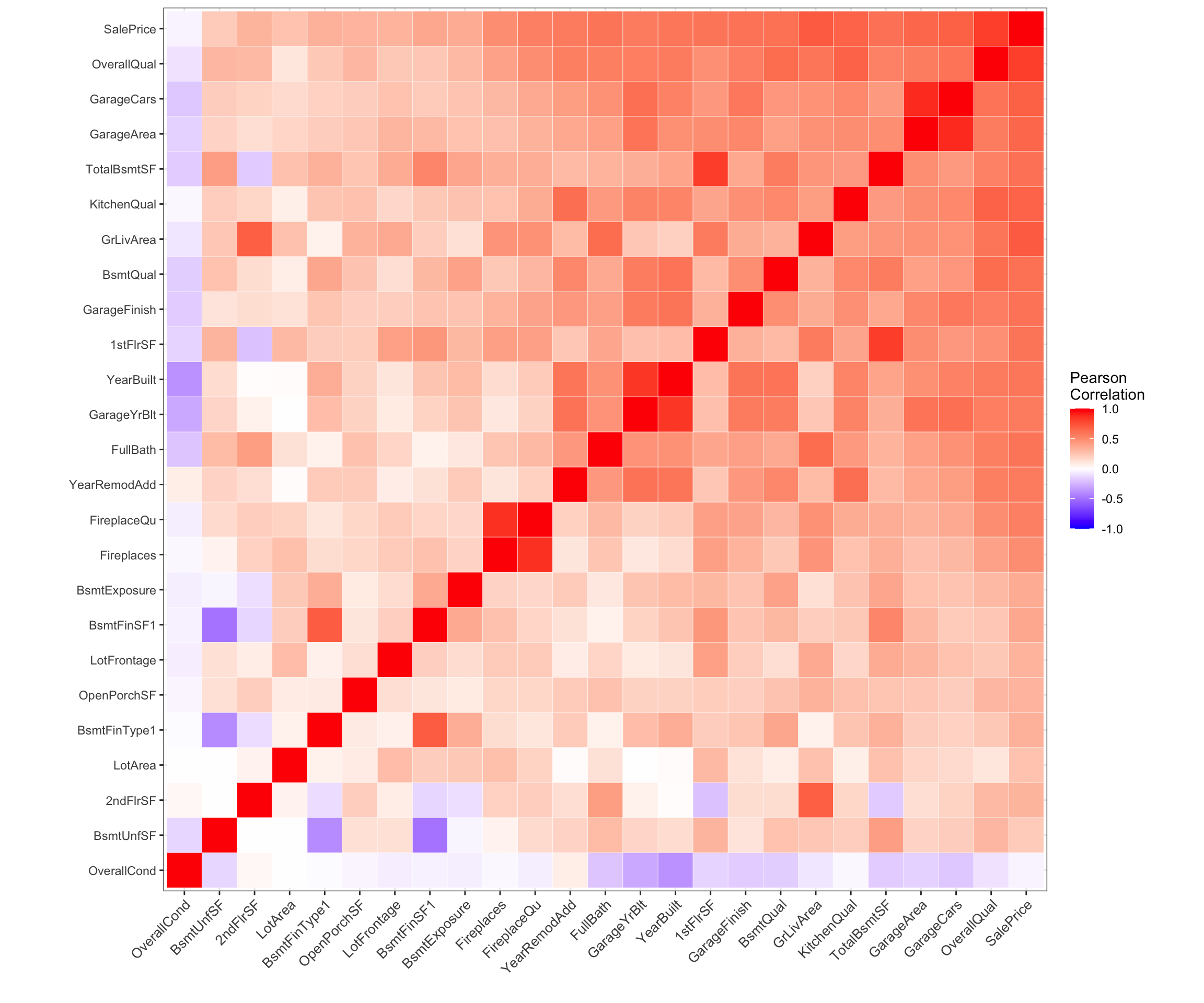
É possível notar que existem variáveis explicativas correlacionadas o que indica que a presença de algumas variáveis pode possivelmente interferir no ajuste final do modelo linear multivariado.
Variáveis categóricas
Já a relação das varáveis categóricas não podem ser calculada com o coeficiente de correlação calculado anteriormente, para avaliar como elas estão associadas será calculado a medida de associação V de Cramér. Novamente a matrix dos resultados serão novamente apresentados em um Heatmap (ou mapa de calor ) que foi inspirado neste post (neste post também é apresentada uma função para o cálculo da matrix, adaptei de forma que se tornasse mais geral e disponibilizei no meu github neste link).
# Carrega funcao que calcula o V de Cramer:
devtools::source_url("https://raw.githubusercontent.com/gomesfellipe/functions/master/cv_test.R")
# Carrega a funcao que realiza as interações dos calculos dois a dois:
devtools::source_url("https://raw.githubusercontent.com/gomesfellipe/functions/master/interaction_all.R")Veja:
cvmat <-
train %>%
select_if(~!is.numeric(.x)) %>%
as.data.table() %>%
interaction_all(cv_test) %>%
as_tibble()
cvmat %>%
ggplot( aes(variable_x, variable_y, fill=v_cramer))+
geom_tile(color="white")+
scale_fill_gradient2(low="blue", high="red", mid="white", midpoint=0, limit=c(-1,1), space="Lab", name="Cramer's V")+
theme_bw()+
theme(axis.text.x=element_text(angle=45, vjust=1, size=10, hjust=1))+
coord_fixed()+
labs(x="",y="")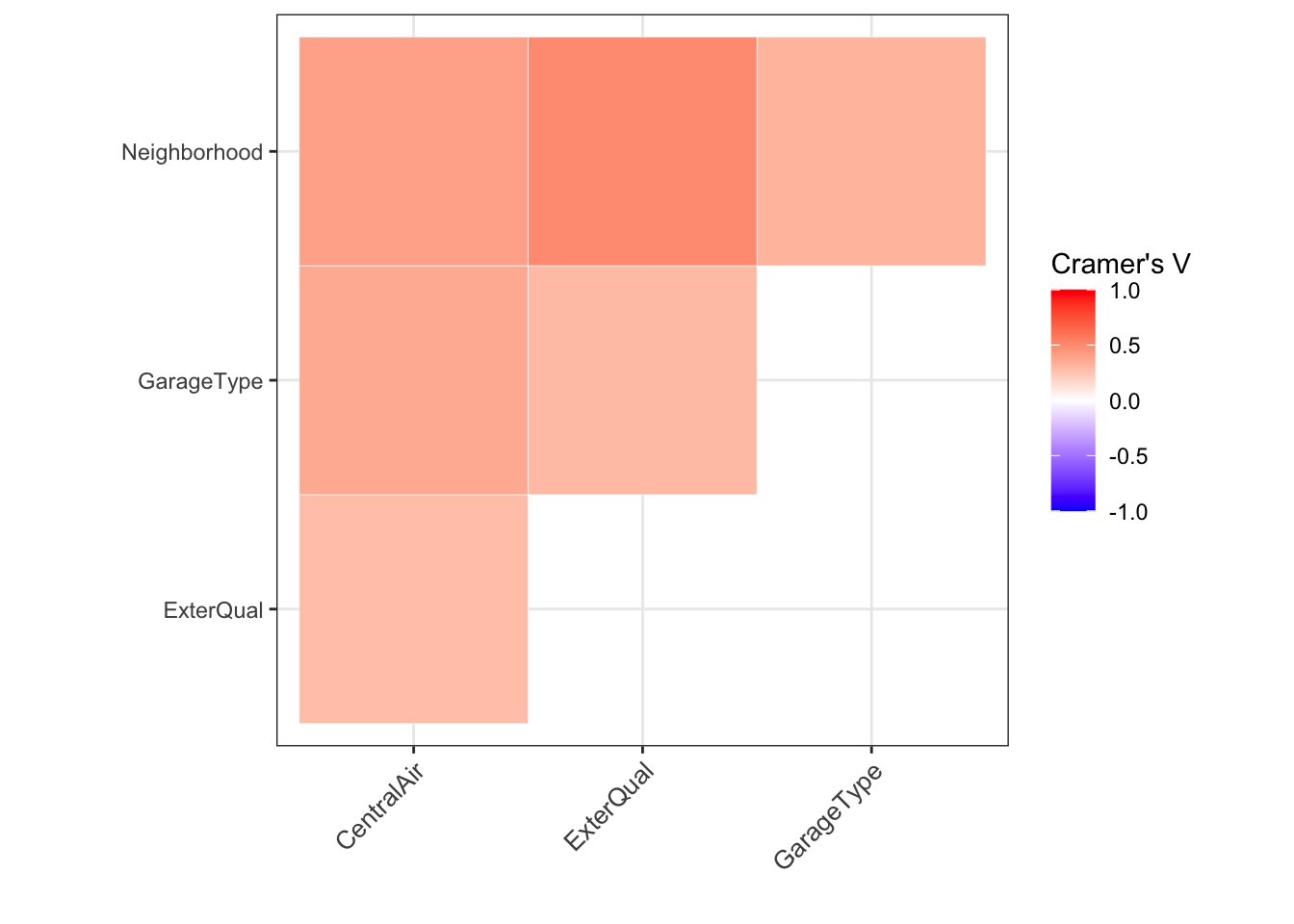
Ajustando modelos
Arvore de decisao
O modelo de árvore de decisão já foi comentado e deixei algumas referências ao final do post portanto vejamos a seguir o ajusto no R. Segundo a documentação:
cp: parâmetro de complexidade. No nosso caso isso significa que o \(R^2\) total deve aumentar em cp em cada etapa. O principal papel desse parâmetro é economizar tempo de computação removendo as divisões que obviamente não valem a pena. Essencialmente, informamos ao programa que qualquer divisão que não melhore o ajuste por cp provavelmente será eliminada por validação cruzada, e que, portanto, o programa não precisa buscá-la.
Para pesquisa de grade existem duas maneiras de ajustar um algoritmo no pacote caret: permitir que o sistema faça isso automaticamente ou especificar o tuneGride manualmente onde cada parâmetro do algoritmo pode ser especificado como um vetor de valores possíveis. Confira o ajuste manual em R:
set.seed(1)
control <- trainControl(method = "cv", number = 5,verboseIter = F)
tunegrid <- expand.grid(cp=seq(0.001, 0.01, 0.001))
rpartFit2 <-
train(y=train$SalePrice, x=train[,-1],
method="rpart",
trControl=control,
tuneGrid=tunegrid,
metric = "Rsquared"
)
rpartFit2## CART
##
## 1460 samples
## 28 predictor
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 1169, 1169, 1168, 1168, 1166
## Resampling results across tuning parameters:
##
## cp RMSE Rsquared MAE
## 0.001 0.1918932 0.7757730 0.1386651
## 0.002 0.1943654 0.7690391 0.1410967
## 0.003 0.2016485 0.7513005 0.1457213
## 0.004 0.2029596 0.7462748 0.1457752
## 0.005 0.2098812 0.7279462 0.1534384
## 0.006 0.2090073 0.7291130 0.1539830
## 0.007 0.2110066 0.7227211 0.1544402
## 0.008 0.2120734 0.7198280 0.1555415
## 0.009 0.2142488 0.7143975 0.1570535
## 0.010 0.2148236 0.7126454 0.1575360
##
## Rsquared was used to select the optimal model using the largest value.
## The final value used for the model was cp = 0.001.Podemos conferir os resultados novamente de maneira visual:
rpart.plot(rpartFit2$finalModel, cex = 0.5)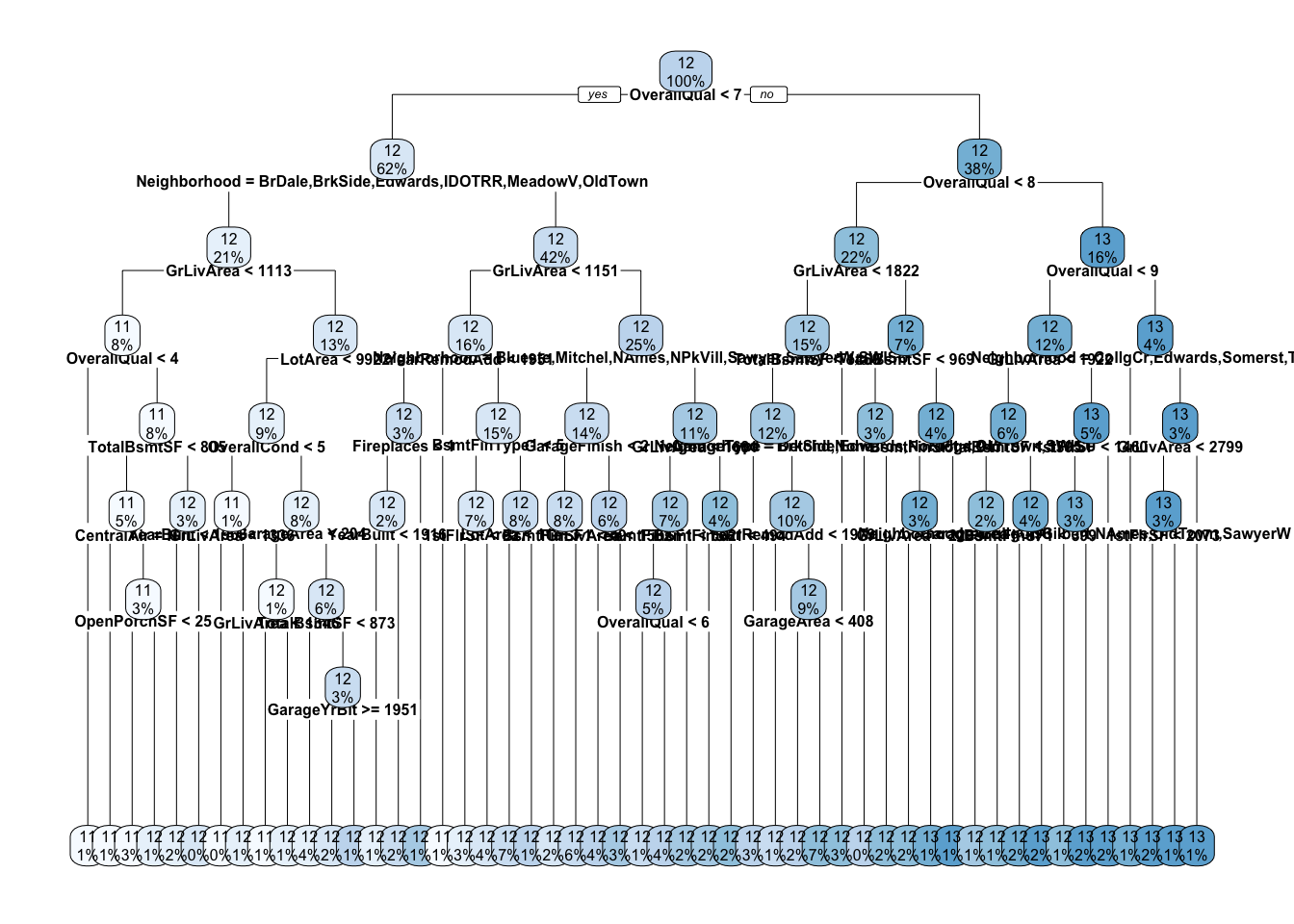
Gerando arquivo para submissão no kaggle:
id %>% cbind(predict(rpartFit2, test) %>% exp) %>%
`colnames<-`(c("Id", "SalePrice")) %>%
write.csv("rpartFit2.csv",row.names = F)Bagging
“Bagging” é usado quando desejamos reduzir a variação de uma árvore de decisão. Ela combina o resultado de vários modelos onde todas as variáveis são considerados para divisão um nó. Em R:
set.seed(1)
control <- trainControl(method = "cv", number = 5,verboseIter = F)
treebagFit <- train(y=train$SalePrice,
x=train[,-1],
method = "treebag",
metric = "Rsquared",
trControl=control
)
treebagFit## Bagged CART
##
## 1460 samples
## 28 predictor
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 1169, 1169, 1168, 1168, 1166
## Resampling results:
##
## RMSE Rsquared MAE
## 0.1831872 0.7946059 0.1288626Note que o \(R^2\) aumentou e o \(RMSE\) diminuiu após o uso desta técnica.
Resultados para enviar para o Kaggle:
id %>% cbind(predict(treebagFit, test)%>% exp) %>%
`colnames<-`(c("Id", "SalePrice")) %>%
write.csv("treebagFit.csv",row.names = F)Random Forest
A principal diferença entre “bagging” e o algoritmo Random Forest é que em randomForest, apenas um subconjunto de características é selecionado aleatoriamente em cada divisão em uma árvore de decisão enquanto que no bagging todos os recursos são usados.
Para pesquisa de grade especificaremos um vetor com os possíveis valores, pois o default adotado para o parâmetro mtry é mtry = p/3 (Número de variáveis amostradas aleatoriamente como candidatos em cada divisão), onde p é o número de variáveis e pode ser que o modelo se ajuste melhor aos dados ao utilizar outro valor.
Veja:
set.seed(1)
tunegrid <- expand.grid(mtry = seq(4, ncol(train) * 0.8, 2))
control <- trainControl(method = "cv", number = 5,verboseIter = F)
rfFit <- train(SalePrice ~. ,
data=train,
method="rf",
metric = "Rsquared",
tuneGrid=tunegrid,
trControl=control
)
rfFit## Random Forest
##
## 1460 samples
## 28 predictor
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 1169, 1169, 1168, 1168, 1166
## Resampling results across tuning parameters:
##
## mtry RMSE Rsquared MAE
## 4 0.1455656 0.8781772 0.09755474
## 6 0.1417368 0.8817193 0.09435674
## 8 0.1405084 0.8826370 0.09350712
## 10 0.1395367 0.8834153 0.09290816
## 12 0.1385338 0.8845102 0.09181049
## 14 0.1386865 0.8840165 0.09223527
## 16 0.1381776 0.8846283 0.09155563
## 18 0.1384532 0.8837305 0.09222536
## 20 0.1380863 0.8840803 0.09173754
## 22 0.1383788 0.8835938 0.09189772
##
## Rsquared was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 16.Note que o \(R^2\) aumentou e o \(RMSE\) apresentou resultados ainda mais satisfatórios.
Veja visualmente a importância de ada variável:
randomForest::varImpPlot(rfFit$finalModel)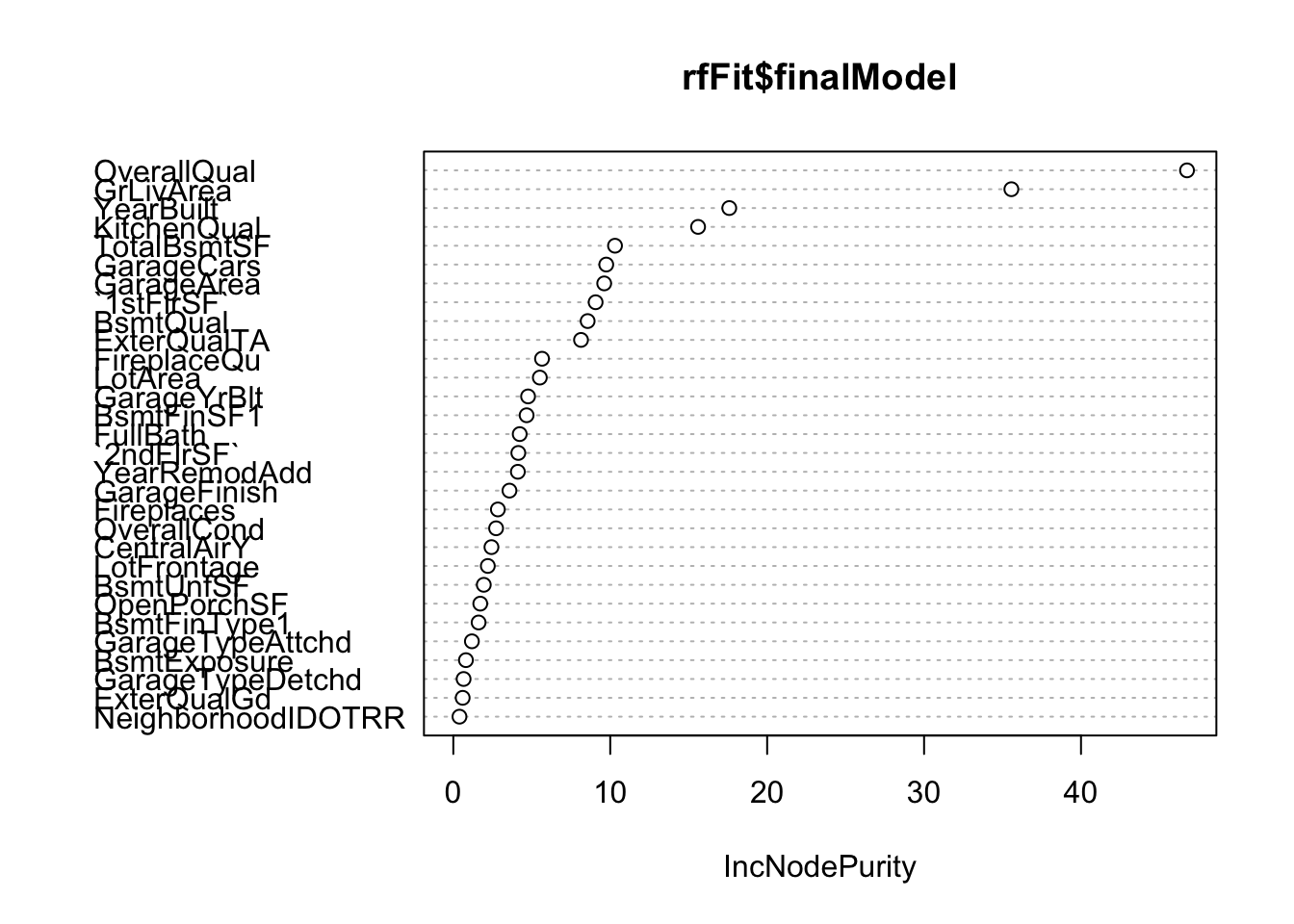
Resultados para enviar para o Kaggle:
id %>% cbind(predict(rfFit, test) %>% exp) %>%
`colnames<-`(c("Id", "SalePrice")) %>%
write.csv("rfFit.csv",row.names = F) GBM
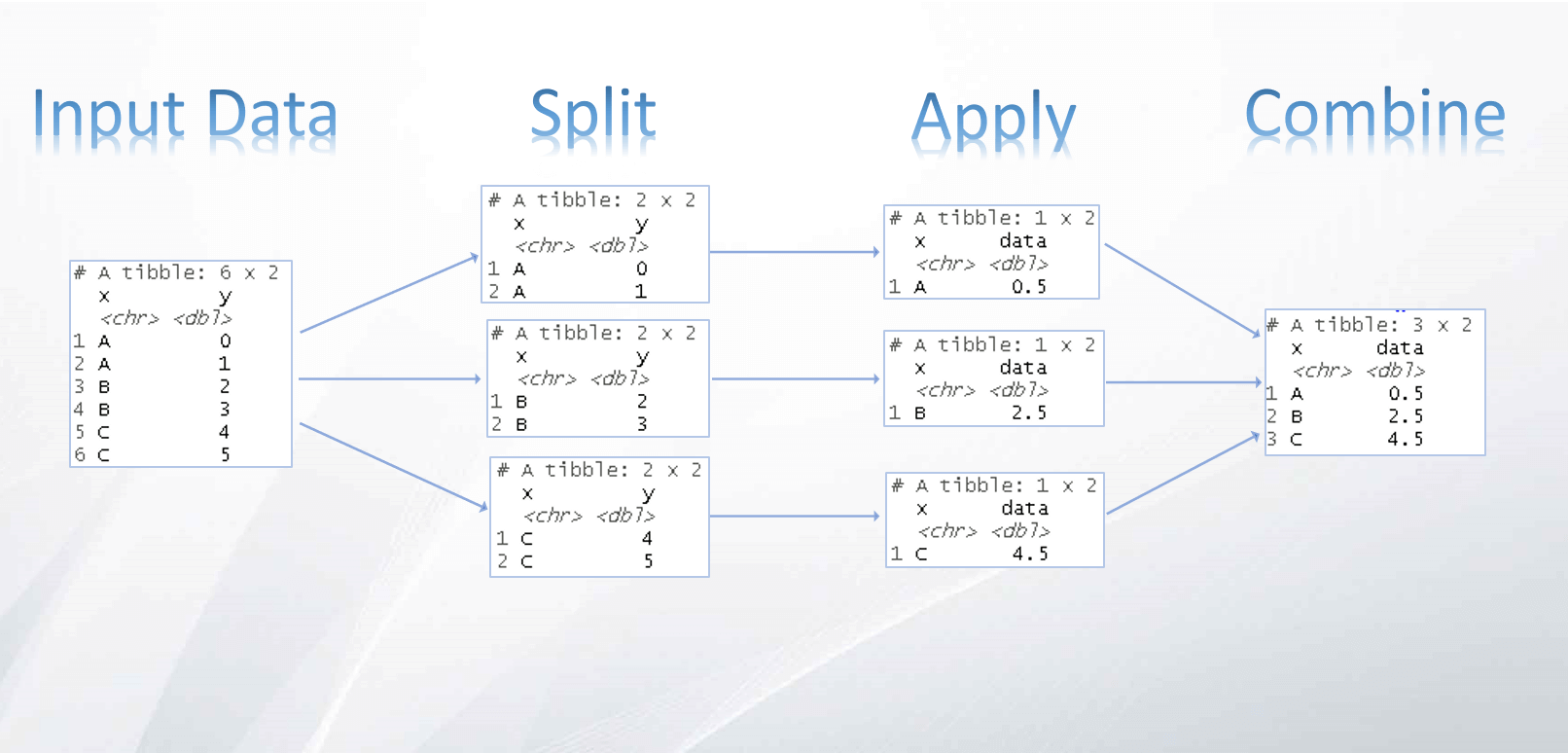
Diferentemente do “bagging”, o “boosting” é uma técnica de ensemble (conjunto) na qual os preditores não são feitos independentemente, mas sequencialmente. Na imagem a seguir é possível ver uma representação visual dessa diferença:
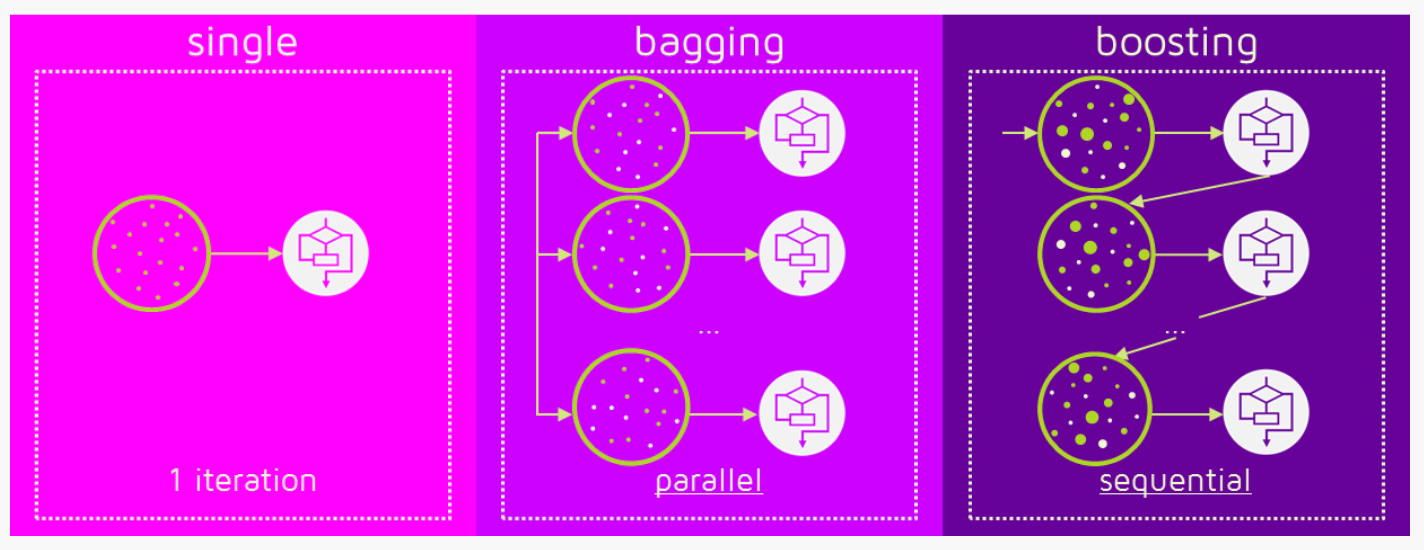
A imagem foi obtida neste artigo: Gradient Boosting from scratch, recomendo a leitura pois da uma boa intuição de como o algoritmo funciona.
Para a pesquisa de grade vamos permitir que o sistema faça isso automaticamente configurando apenas o tuneLength para indicar o número de valores diferentes para cada parâmetro do algoritmo.
set.seed(1)
control <- trainControl(method = "cv", number = 5,verboseIter = F)
gbmFit <- train(SalePrice~.,data=train,
method = "gbm",
trControl=control,
tuneLength=5,
metric = "Rsquared",
verbose = FALSE
)
gbmFit## Stochastic Gradient Boosting
##
## 1460 samples
## 28 predictor
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 1169, 1169, 1168, 1168, 1166
## Resampling results across tuning parameters:
##
## interaction.depth n.trees RMSE Rsquared MAE
## 1 50 0.1736970 0.8346902 0.12145158
## 1 100 0.1474386 0.8663694 0.10371271
## 1 150 0.1400060 0.8775141 0.09804851
## 1 200 0.1381902 0.8803999 0.09607709
## 1 250 0.1375854 0.8817130 0.09502881
## 2 50 0.1511051 0.8640075 0.10557294
## 2 100 0.1379357 0.8815852 0.09546142
## 2 150 0.1360260 0.8846503 0.09326628
## 2 200 0.1355702 0.8852090 0.09248558
## 2 250 0.1362827 0.8841734 0.09254710
## 3 50 0.1434808 0.8743589 0.09910961
## 3 100 0.1363881 0.8838715 0.09355652
## 3 150 0.1346606 0.8868808 0.09163759
## 3 200 0.1339427 0.8880370 0.09062153
## 3 250 0.1336666 0.8886732 0.08979366
## 4 50 0.1376575 0.8824442 0.09516571
## 4 100 0.1334392 0.8884173 0.09192150
## 4 150 0.1330866 0.8890336 0.09156893
## 4 200 0.1334706 0.8886198 0.09096598
## 4 250 0.1335809 0.8884950 0.09101981
## 5 50 0.1384852 0.8813449 0.09535954
## 5 100 0.1350803 0.8863344 0.09231165
## 5 150 0.1340246 0.8878172 0.09112111
## 5 200 0.1342892 0.8874590 0.09088714
## 5 250 0.1349331 0.8867525 0.09104875
##
## Tuning parameter 'shrinkage' was held constant at a value of 0.1
##
## Tuning parameter 'n.minobsinnode' was held constant at a value of 10
## Rsquared was used to select the optimal model using the largest value.
## The final values used for the model were n.trees = 150, interaction.depth =
## 4, shrinkage = 0.1 and n.minobsinnode = 10.Note que este foi o modelo que apresentou os melhores resultados quanto só \(R^2\) e ao \(RMSE\) em comparação com os outros modelos.
Submissão para Kaggle:
id %>% cbind(predict(gbmFit, test) %>% exp) %>%
`colnames<-`(c("Id", "SalePrice")) %>%
write.csv("gbmFit.csv", row.names = F)Regressão Linear
Por fim faremos o ajuste de um modelo de regressão linear multivariado utilizando o pacote caret.
Utilizaremos validação cruzada separando nossa amostra em 5 e utilizaremos o método lmStepAIC que realiza a seleção do modelo escalonado pelo critério de informação de Akaike - AIC.
set.seed(1)
control <- trainControl(method = "cv", number = 5,verboseIter = F)
lmFit <- train(SalePrice~.,data=train,
method = "lmStepAIC",
trControl=control,
metric = "Rsquared",trace=F
)
lmFit## Linear Regression with Stepwise Selection
##
## 1460 samples
## 28 predictor
##
## No pre-processing
## Resampling: Cross-Validated (5 fold)
## Summary of sample sizes: 1169, 1169, 1168, 1168, 1166
## Resampling results:
##
## RMSE Rsquared MAE
## 0.147716 0.8632513 0.09574552Note que o ajuste do modelo se apresenta de maneira satisfatória com \(R^2\) e \(RMSE\) semelhantes aos modelos de bagging e boosting e além disso, diferente dos modelos baseados em árvore, com este ajuste é possível notar a significância estatística de cada parâmetro ajustado, o que possibilita tanto o uso tanto como modelo preditivo quanto como modelo descritivo. Veja:
ggcoef(
lmFit$finalModel, #O modelo a ser conferido
vline_color = "red", #Reta em zero
errorbar_color = "blue", #Cor da barra de erros
errorbar_height = .25,
shape = 18, #Altera o formato dos pontos centrais
size=2, #Altera o tamanho do ponto
color="black",
exclude_intercept = TRUE, #Altera a cor do ponto
mapping = aes(x = estimate, y = term, size = p.value))+
scale_size_continuous(trans = "reverse")+ #Essa linha faz com que inverta o tamanho
theme_bw()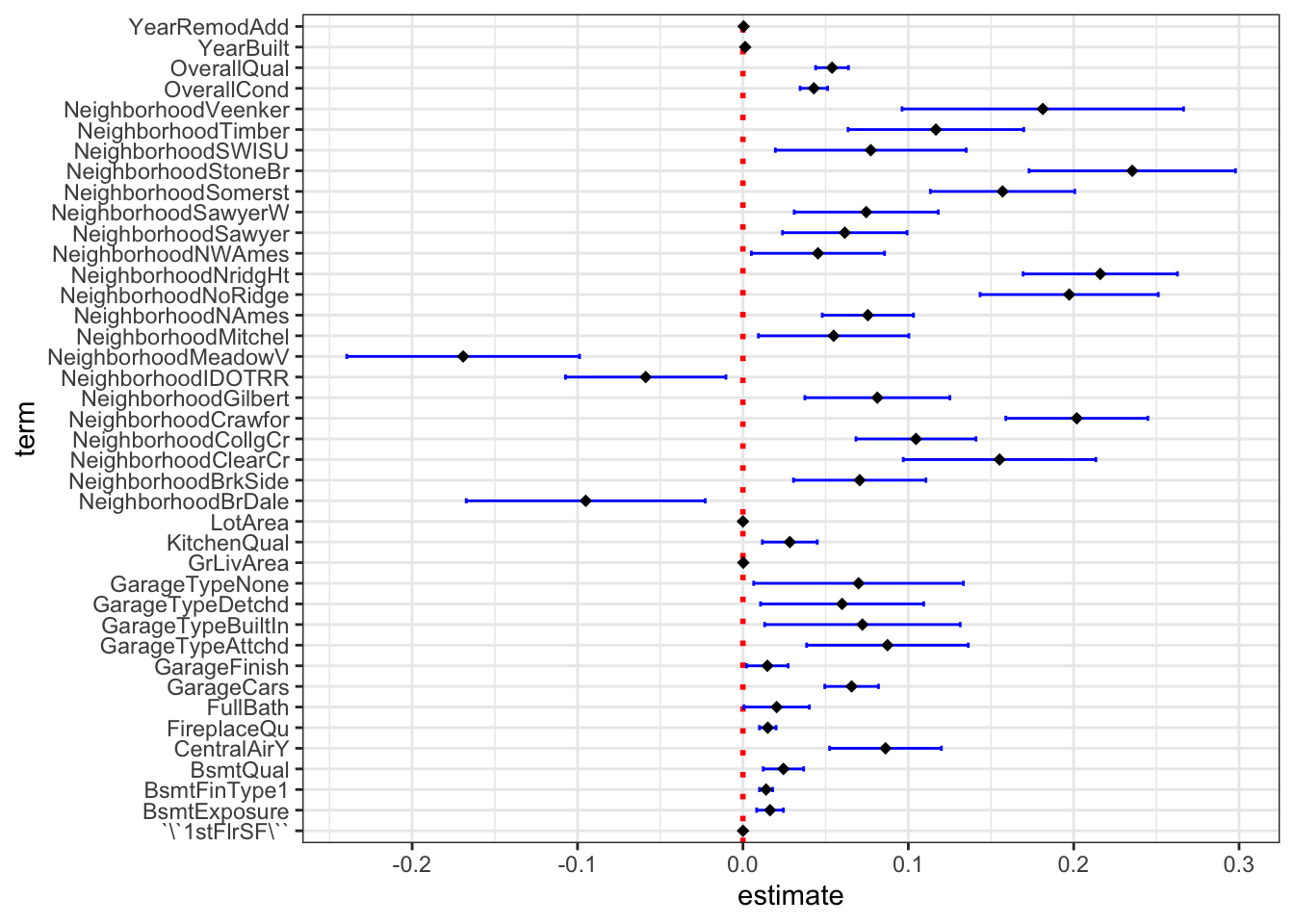
Note que o intercepto \(\beta_0\) foi retirado da imagem pois é muito superior aos demais coeficientes. Note também que \(\beta_i\) informa quão sensível é \(y\), no caso log(SalePrice) às variações de cara umas das \(x_{i,j}\) variáveis explicativas. Mais concretamente, se \(x_{i,j}\) aumenta em uma unidade, o valor de \(y\) varia em \(\beta_1\) unidades.
Uma rápida Análise dos Resíduos:
lmFit$finalModel %>%
autoplot(which = 1:2) +
theme_bw()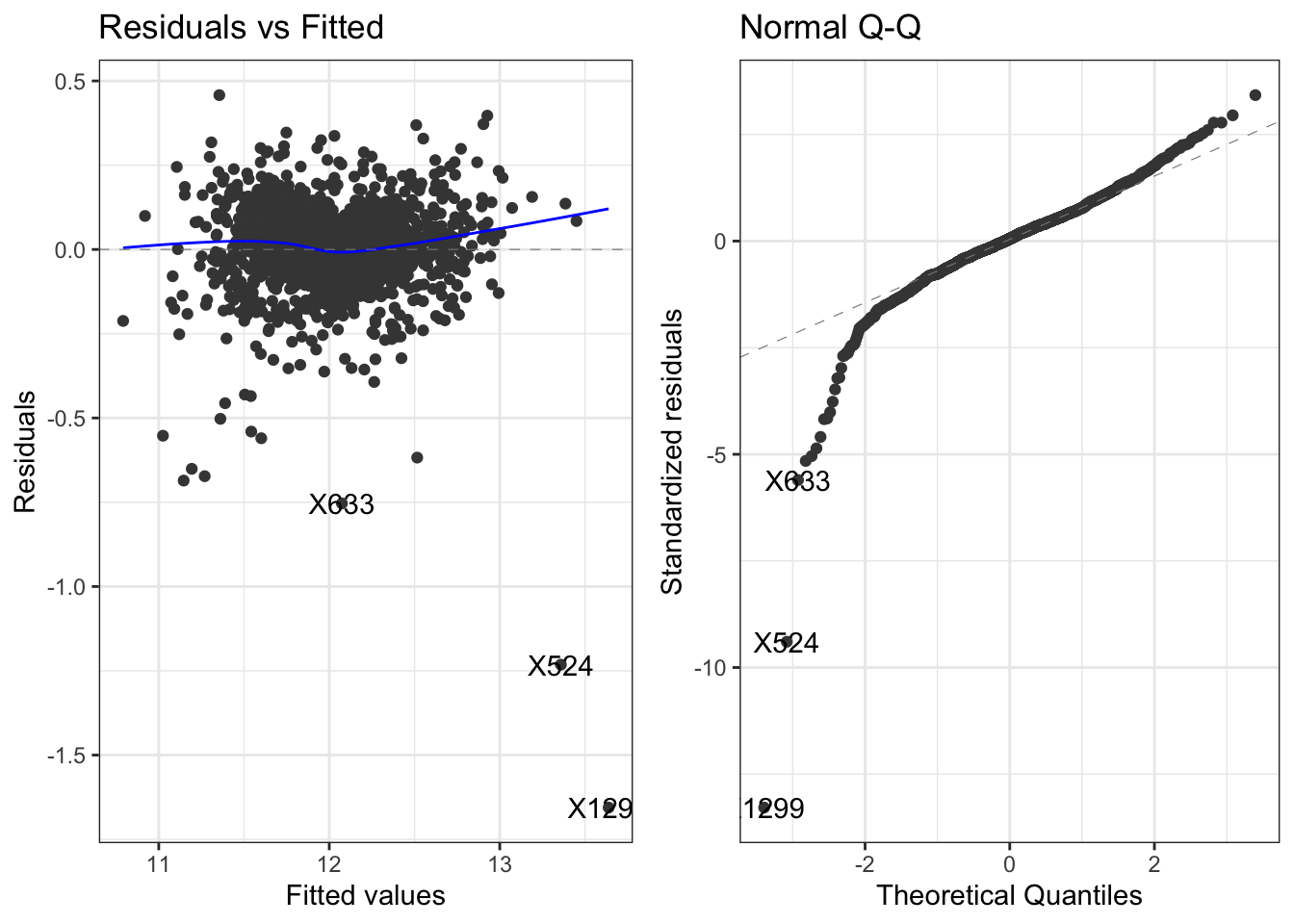
É possível notar que parece haver alguns outliers em ambas as figuras. Na primeira é possível notar uma nuvem de pontos aleatórios em torno de zero porém na segunda figura nota-se que alguns valores não estão de acordo com os quantils teóricos de uma distribuição normal, o que pode prejudicar nossa interpretação dos coeficientes do modelo. Vamos encerrar o modelo por aqui mesmo e ver como ele se sai na competição do Kaggle, preparando a submissão:
id %>% cbind(predict(lmFit, test) %>% exp ) %>%
`colnames<-`(c("Id", "SalePrice")) %>%
write.csv("lmFit.csv",row.names = F)O score obtido com esta submissão no Kaggle foi muito próximo dos modelos baseados e árvore e o tempo computacional para este ajuste foi bem menor.
Comparando ajustes
Vejamos a seguir uma comparação entre estes modelos com as funções fornecidas pelo pacote `caret:.
resamps <- resamples(list(rpart = rpartFit2,
treebag = treebagFit,
rf = rfFit,
gbm = gbmFit,
lm = lmFit
))
bwplot(resamps)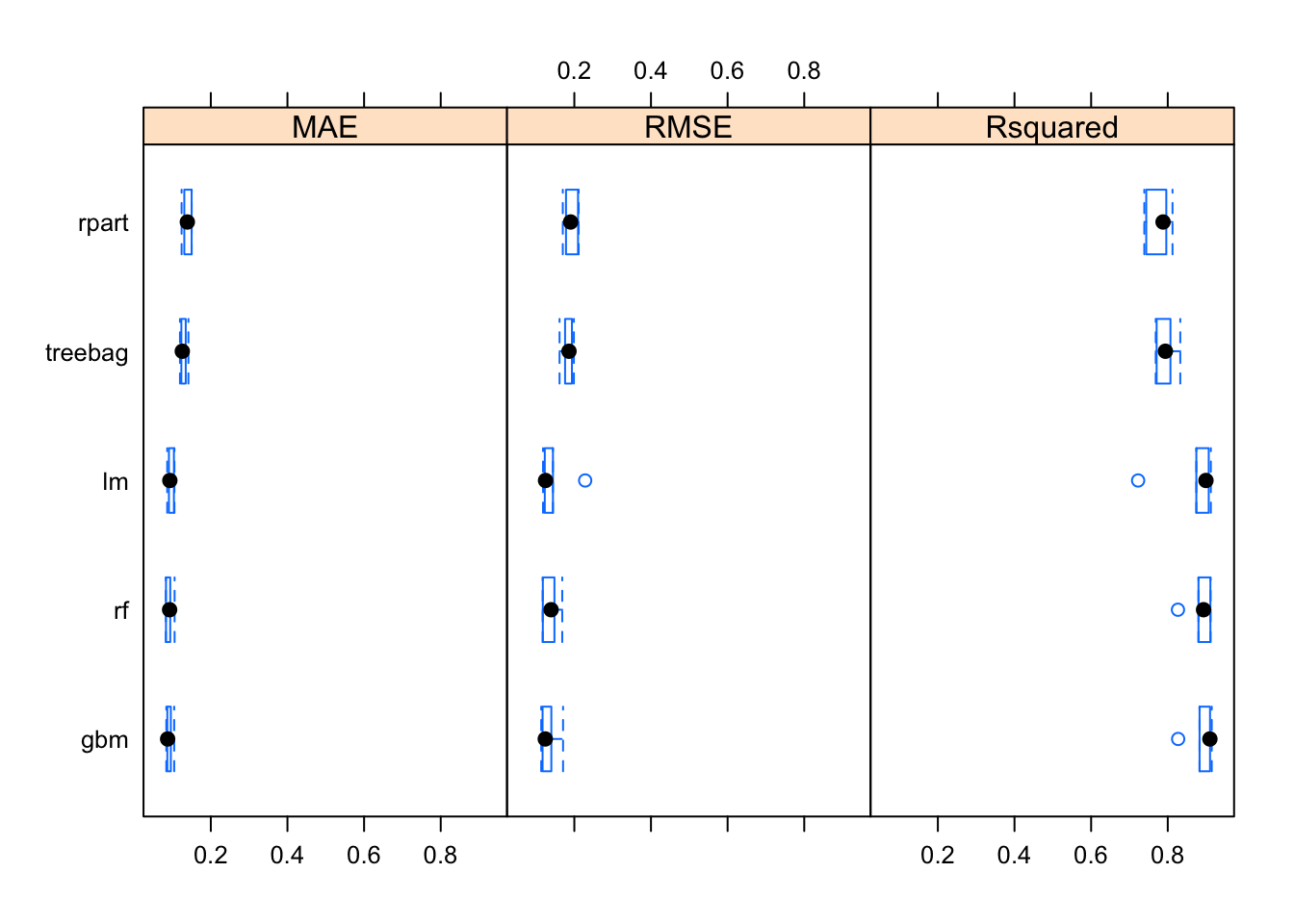
Com este gráfico é possível notar que o modelo de regressão linear múltipla apresentou resultados semelhantes aos de bagging e boosting.
É importante frisar que a maneira como as variáveis foram selecionadas para o modelo de regressão linear múltipla através da importância das variáveis obtida com o modelo randomForest não é um padrão e existem diversos outros modos estatísticos de se de determinar a significância e a relação das variáveis para o modelo.
Um possível problema neste método é que não detecta a multicolinearidade, que ocorre quando as variáveis explicativas estão fortemente correlacionadas entre si e a análise de regressão linear pode ficar confusa e desprovida de significado, pois há dificuldade em distinguir o efeito de uma ou outra variável explicativa sobre a variável resposta \(Y\) devido à variâncias muito elevadas ou sinais inconsistentes.
Essa proposta de aprender se divertindo e de maneira produtiva me deixa muito empolgado, espero que tenham se divertido como eu me diverti fazendo este post!
Referências:
- DataCamp Course:Machine Learning with Tree-Based Models in R
- Data Science for Business
- Learn ML Algorithms by coding: Decision Trees
- DataCamp Tutorials: Decision Trees in R
- The caret Package - Max Kuhn
- Um tutorial completo sobre modelagem baseada em árvores de decisão (códigos R e Python)
- Tuning Machine Learning Models Using the Caret R Package
- Gradient Boosting from scratch
- Tune Machine Learning Algorithms in R (random forest case study)
- Random Forests - Leo Breiman and Adele Cutler
- An Introduction to Recursive Partitioning Using the RPART Routines - CRAN






























Share this post
Twitter
LinkedIn
Email