AED de forma rápida e um pouco de Machine Learning
Veja como é possível realizar a AED de forma muito rápida com o pacote SmartEAD, além de uma breve aplicação de técnicas de machine learning e estatística para ilustrar alguns possíveis cenários da analise da dados
A análise exploratória dos dados
A análise exploratória dos dados (AED) foi um termo que ganhou bastante popularidade quando Tukey publicou o livro Exploratory Data Analysis em 1977 que tratava uma “busca por conhecimento antes da análise de dados de fato”. Ocorre quando busca-se obter informações ocultas sobre os dados, tais como: variação, anomalias, distribuição, tendências, padrões e relações
Ao iniciar uma análise de dados, começamos pela AED para a partir dai decidir como buscar qual solução para o problema. É importante frisar que a AED e a construção de gráficos não são a mesma coisa, mesmo a AED sendo altamente baseada em produção de gráficos como de dispersão, histogramas, boxplots etc.
Por vezes a AED no R pode envolver a produção de longos scripts utilizando funções como as do pacote ggplot2 e mesmo sabendo que desejamos sempre criar o gráfico de maneira mais informativa e atraente possível, as vezes precisamos ter uma noção geral dos dados de forma rápida, não necessariamente tão detalhada e customizada de cara.
A vezes queremos apenas ter uma primeira impressão dos dados e em seguida pensar em quais os gráficos mais se adequariam para a entrega dos resultados que mesmo as funções base do R dependendo do caso também envolvem a confecção de longos scripts.
Existem pacotes que auxiliam na hora de se fazer uma rápida análise exploratória, como o skimr e o DataExplorer. Porém estava pesquisando de existiam mais opções para uma rápida abordagem de AED e me deparei com esta vinheta, por Dayanand, Kiran, Ravi.
Essa vinheta apresenta o pacote SmartEAD que trás uma série de funções que auxiliam na AED de forma bem prática. O pacote está disponível no CRAN.
Para testar o pacote foi utilizada uma base de dados do artigo A Theory of Extramarital Affairs, publicado pela The University of Chicago Press.
Gostei tanto da proposta do pacote que resolvi preparar este post que conta com a explanação de alguns tópicos apresentados pelo autor, algumas explicações da teoria estatística apresentada na análise descritiva e exploratória dos dados e além da aplicação de algumas técnicas estatísticas e de machine learning para o entendimento da base de dados.
SmartEDA
Como ele pode ajudá-lo a criar uma análise de dados exploratória? O SmartEDA inclui várias funções personalizadas para executar uma análise exploratória inicial em qualquer dado de entrada. A saída gerada pode ser obtida em formato resumido e gráfico e os resultados também podem ser exportados como relatórios.
O pacote SmartEDA ajuda a construir uma boa base de compreensão de dados, algumas de suas funcionalidades são:
- O pacote SmartEDA fará com que você seja capaz de aplicar diferentes tipos de EDA sem ter que lembre-se dos diferentes nomes dos pacotes R e escrever longos scripts R com esforço manual para preparar o relatório da EDA, permitindo o entendimento dos dados de maneira mais rápida
- Não há necessidade de categorizar as variáveis em caractere, numérico, fator etc. As funções do SmartEDA categorizam automaticamente todos os recursos no tipo de dados correto (caractere, numérico, fator etc.) com base nos dados de entrada.
O pacote SmartEDA ajuda a obter a análise completa dos dados exploratórios apenas executando a função em vez de escrever um longo código r.
Carregando o pacote:
# install.packages("SmartEDA")
library("SmartEDA")outros pactes que serão utilizados no post (incluindo um script com algumas funções, que estará disponível no meu github neste link).
library(knitr) # Para tabelas interativas
library(DT) # Para tabelas interativas
library(dplyr) # Para manipulacao de dados
library(plotly) # Para gerar uma tabela
library(psych) # para análise fatorial
source("functions.R") # script com funcoes customizadasBase de dados utilizada:
Estava à procura de uma base de dados para testar as funcionalidades do pacote SmartEAD quando um colega de trabalho me mostrou um artigo chamado A Theory of Extramarital Affairs, publicado pela The University of Chicago Press. Neste artigo é desenvolvido um modelo pelo estimador de Tobit que explica a alocação de um tempo do indivíduo entre o trabalho e dois tipos de atividades de lazer: tempo passou com o cônjuge e tempo gasto com o amante.
Não conhecia o modelo proposto e em uma rápida pesquisa no Google notei que alguns dos dados utilizados nesse artigo estão disponíveis no pacote AER de Econometria Aplicada com R, que contém funções, conjuntos de dados, exemplos, demonstrações e vinhetas para o livro Applied Econometrics with R e como esses dados já foram tratados e estão “prontos para análise”, resolvi usar essa amostra pela conveniência.
Portanto farei aqui uma análise exploratória e ao final de cada caso (sem variável reposta, com variável resposta numérica e com variável resposta binária), para ter uma breve intuição de como se comportam os dados irei primeiro utilizar um algorítimo de machine learning não supervisionado para o agrupamento das observações (sem considerar q já conhecemos a variável resposta), depois ajustar um* modelo de regressão linear simples* considerando a variável resposta como numérica e por fim o ajuste de um algorítimo de machine learning supervisonado de classificação após discretizar a variável resposta.
A base de dados pode ser conferida a seguir:
library(AER)
data(Affairs)
Affairs %>% rmarkdown::paged_table()Neste post, a análise de dados será feita considerando a variável affairs (Quantas vezes envolvido em caso extraconjugal no último ano (aparentemente em 1977)) e a base de dados conta com as variáveis gênero, idade, anos de casado, se tem crianças, religiosidade, educação, ocupação e como avalia o casamento.
Informações detalhadas podem ser conferidas na tabela a seguir, retirada do artigo apresentado:

Obs.: Essa tabela foi feita com o pacote plotly, o código pode ser conferido aqui.
Visão geral dos dados
Entendendo as dimensões do conjunto de dados, nomes de variáveis, resumo geral, variáveis ausentes e tipos de dados de cada variável com a função ExpData(), se o argumento Type = 1, visualização dos dados (os nomes das colunas são “Descrições”, “Obs.”), já se Type = 2, estrutura dos dados (os nomes das colunas são “S.no”, “VarName”, “VarClass”, “VarType”)
:
# Visao geral dos dados - Type = 1
ExpData(data=Affairs, type=1) # O tipo 1 é uma visão geral dos dados## Descriptions Value
## 1 Sample size (nrow) 601
## 2 No. of variables (ncol) 9
## 3 No. of numeric/interger variables 7
## 4 No. of factor variables 2
## 5 No. of text variables 0
## 6 No. of logical variables 0
## 7 No. of identifier variables 0
## 8 No. of date variables 0
## 9 No. of zero variance variables (uniform) 0
## 10 %. of variables having complete cases 100% (9)
## 11 %. of variables having >0% and <50% missing cases 0% (0)
## 12 %. of variables having >=50% and <90% missing cases 0% (0)
## 13 %. of variables having >=90% missing cases 0% (0)Conferindo o nome das variáveis e os tipos de cada uma:
# Estrutura dos dados - Type = 2
ExpData(data=Affairs, type=2) # O tipo 2 é a estrutura dos dados## Index Variable_Name Variable_Type Per_of_Missing No_of_distinct_values
## 1 1 affairs numeric 0 6
## 2 2 gender factor 0 2
## 3 3 age numeric 0 9
## 4 4 yearsmarried numeric 0 8
## 5 5 children factor 0 2
## 6 6 religiousness integer 0 5
## 7 7 education numeric 0 7
## 8 8 occupation integer 0 7
## 9 9 rating integer 0 5Esta função fornece visão geral e estrutura dos quadros de dados.
Análise exploratória dos dados
As funções a seguir apresentam a saída EDA para 3 casos diferentes de análise exploratória dos dados, são elas:
A variável de destino não está definida
A variável alvo é contínua
A variável de destino é categórica
Para fins ilustrativos, será feita inicialmente uma análise considerando que não existe variável resposta, em seguida será considerada a variável affairs como variável resposta e por fim, será feita uma transformação nesta variável resposta numérica de forma que ela seja discretizada da seguinte maneira:
\[ 1 \text{ se já houve caso extraconjugal} \\ 0 \text{ se não houve caso extraconjugal} \]
Relatório em uma linha
Caso o interesse seja apenas ter uma noção geral dos dados de forma extremamente rápida, basta rodar a linha de código abaixo:
ExpReport(Affairs,op_file = "teste.html")Antes de começar a explanar cada um dos casos, achei que seria legal frisar que além de tudo que será apresentado, existe a opção de se obter um relatório extenso sobre a análise exploratória dos dados em apenas uma linha!
Exemplo para o caso 1: a variável de destino não está definida
Para ilustrar o primeiro caso, onde a variável destino não é definida, vamos supor que não existe uma variável alvo na nossa base de dados e estamos interessados em simplesmente obter uma visão geral enquanto pensamos em quais técnicas estatísticas serão utilizadas para avaliar nosso dataset.
Resumo das variáveis numéricas
Resumo de de todas as variáveis numéricas:
ExpNumStat (Affairs,
by = "A", # Agrupar por A (estatísticas resumidas por Todos), G (estatísticas resumidas por grupo), GA (estatísticas resumidas por grupo e Geral)
gp = NULL, # variável de destino, se houver, padrão NULL
MesofShape = 2, # Medidas de formas (assimetria e curtose).
Outlier = TRUE, # Calcular o limite inferior, o limite superior e o número de outliers
round = 2) # Arredondar## Vname Group
## 1 1 AllPodemos ver que não existem variáveis negativas e a única variável que apresentou “zero” foi a variável resposta. Nenhum registro como Inf ou como NA e além das medidas descritivas também podemos notar as medidas de skweness e kurtosis. Alguns comentários sobre essas medidas:
Medidas de forma para dar uma avaliação detalhada dos dados. Explica a quantidade e a direção do desvio.
- Kurotsis explica o quão alto e afiado é o pico central (Achatamento).
- Skewness não tem unidades: mas um número, como um escore z (medida da assimetria)
Onde:
A curtose é uma medida de forma que caracteriza o achatamento da curva da função de distribuição de probabilidade, Assim:
- Se o valor da curtose for = 0 (ou 3, pela segunda definição), então tem o mesmo achatamento que a distribuição normal. Chama-se a estas funções de mesocúrticas
- Se o valor é > 0 (ou > 3), então a distribuição em questão é mais alta (afunilada) e concentrada que a distribuição normal. Diz-se que esta função probabilidade é leptocúrtica, ou que a distribuição tem caudas pesadas (o significado é que é relativamente fácil obter valores que não se aproximam da média a vários múltiplos do desvio padrão)
- Se o valor é < 0 (ou < 3), então a função de distribuição é mais “achatada” que a distribuição normal. Chama-se-lhe platicúrtica
O Skewness mede a assimetria das caudas da distribuição. Distribuições assimétricas que tem uma cauda mais “pesada” que a outra apresentam obliquidade. Distribuições simétricas tem obliquidade zero. Assim:
- Se v>0, então a distribuição tem uma cauda direita (valores acima da média) mais pesada
- Se v<0, então a distribuição tem uma cauda esquerda (valores abaixo da média) mais pesada
- Se v=0, então a distribuição é aproximadamente simétrica (na terceira potência do desvio em relação à média).
Distribuições de variáveis numéricas
Representação gráfica de todos os recursos numéricos com gráfico de densidade (uni variada):
# Nota: Variável excluída (se o valor único da variável for menor ou igual a 10 [im = 10])
ExpNumViz(Affairs,
Page=c(2,2), # padrão de saída.
sample=NULL) # seleção aleatória de plots## $`0`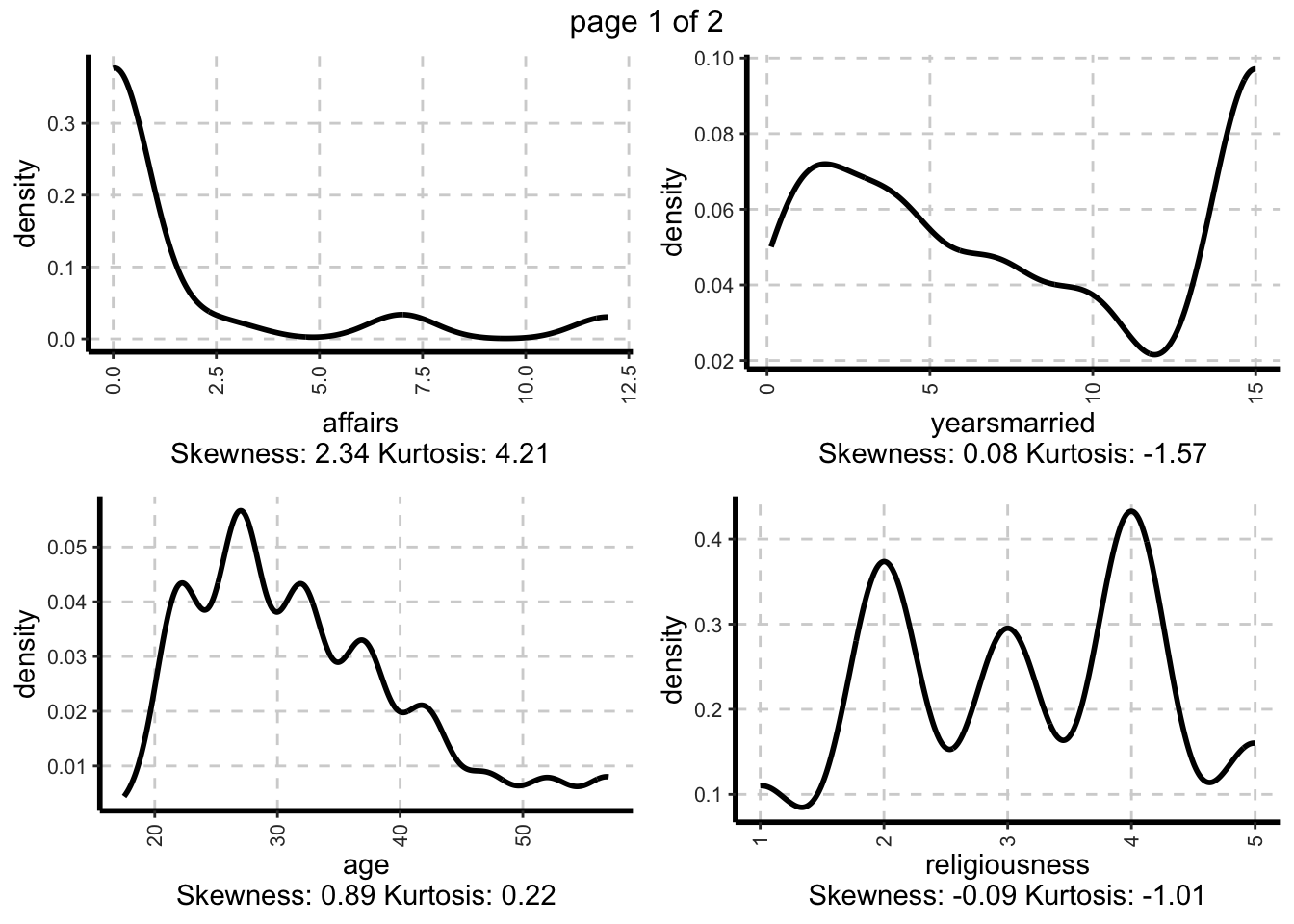

Exibidos os gráficos com as densidades das variáveis numéricas. Como podemos ver a maioria da amostra não registrou caso extraconjugal, a maioria tem de 12 ou mais anos de casado. A média amostral da idade dos indivíduos é de aproximadamente 32 anos apresentando leve assimetria com cauda a direita. As demais variáveis podem ser conferidas visualmente.
Resumo de variáveis categóricas
Essa função selecionará automaticamente variáveis categóricas e gerará frequência ou tabelas cruzadas com base nas entradas do usuário. A saída inclui contagens, porcentagens, total de linhas e total de colunas.
Frequência para todas as variáveis independentes categóricas:
ExpCTable(Affairs,
Target=NULL)## Variable Valid Frequency Percent CumPercent
## 1 gender female 315 52.41 52.41
## 2 gender male 286 47.59 100.00
## 3 gender TOTAL 601 NA NA
## 4 children no 171 28.45 28.45
## 5 children yes 430 71.55 100.00
## 6 children TOTAL 601 NA NA
## 7 affairs 0 451 75.04 75.04
## 8 affairs 1 34 5.66 80.70
## 9 affairs 12 38 6.32 87.02
## 10 affairs 2 17 2.83 89.85
## 11 affairs 3 19 3.16 93.01
## 12 affairs 7 42 6.99 100.00
## 13 affairs TOTAL 601 NA NA
## 14 age 17.5 6 1.00 1.00
## 15 age 22 117 19.47 20.47
## 16 age 27 153 25.46 45.93
## 17 age 32 115 19.13 65.06
## 18 age 37 88 14.64 79.70
## 19 age 42 56 9.32 89.02
## 20 age 47 23 3.83 92.85
## 21 age 52 21 3.49 96.34
## 22 age 57 22 3.66 100.00
## 23 age TOTAL 601 NA NA
## 24 yearsmarried 0.125 11 1.83 1.83
## 25 yearsmarried 0.417 10 1.66 3.49
## 26 yearsmarried 0.75 31 5.16 8.65
## 27 yearsmarried 1.5 88 14.64 23.29
## 28 yearsmarried 10 70 11.65 34.94
## 29 yearsmarried 15 204 33.94 68.88
## 30 yearsmarried 4 105 17.47 86.35
## 31 yearsmarried 7 82 13.64 99.99
## 32 yearsmarried TOTAL 601 NA NA
## 33 religiousness 1 48 7.99 7.99
## 34 religiousness 2 164 27.29 35.28
## 35 religiousness 3 129 21.46 56.74
## 36 religiousness 4 190 31.61 88.35
## 37 religiousness 5 70 11.65 100.00
## 38 religiousness TOTAL 601 NA NA
## 39 education 12 44 7.32 7.32
## 40 education 14 154 25.62 32.94
## 41 education 16 115 19.13 52.07
## 42 education 17 89 14.81 66.88
## 43 education 18 112 18.64 85.52
## 44 education 20 80 13.31 98.83
## 45 education 9 7 1.16 99.99
## 46 education TOTAL 601 NA NA
## 47 occupation 1 113 18.80 18.80
## 48 occupation 2 13 2.16 20.96
## 49 occupation 3 47 7.82 28.78
## 50 occupation 4 68 11.31 40.09
## 51 occupation 5 204 33.94 74.03
## 52 occupation 6 143 23.79 97.82
## 53 occupation 7 13 2.16 99.98
## 54 occupation TOTAL 601 NA NA
## 55 rating 1 16 2.66 2.66
## 56 rating 2 66 10.98 13.64
## 57 rating 3 93 15.47 29.11
## 58 rating 4 194 32.28 61.39
## 59 rating 5 232 38.60 99.99
## 60 rating TOTAL 601 NA NAObs.: NA significa Not Applicable
Distribuições de variáveis categóricas
Essa função varre automaticamente cada variável e cria um gráfico de barras para variáveis categóricas.
Gráficos de barra para todas as variáveis categóricas
ExpCatViz(Affairs,
fname=NULL, # Nome do arquivo de saida, default é pdf
clim=10,# categorias máximas a incluir nos gráficos de barras.
margin=2,# índice, 1 para proporções baseadas em linha e 2 para proporções baseadas em colunas
Page = c(2,1), # padrao de saida
sample=4) # seleção aleatória de plot## $`0`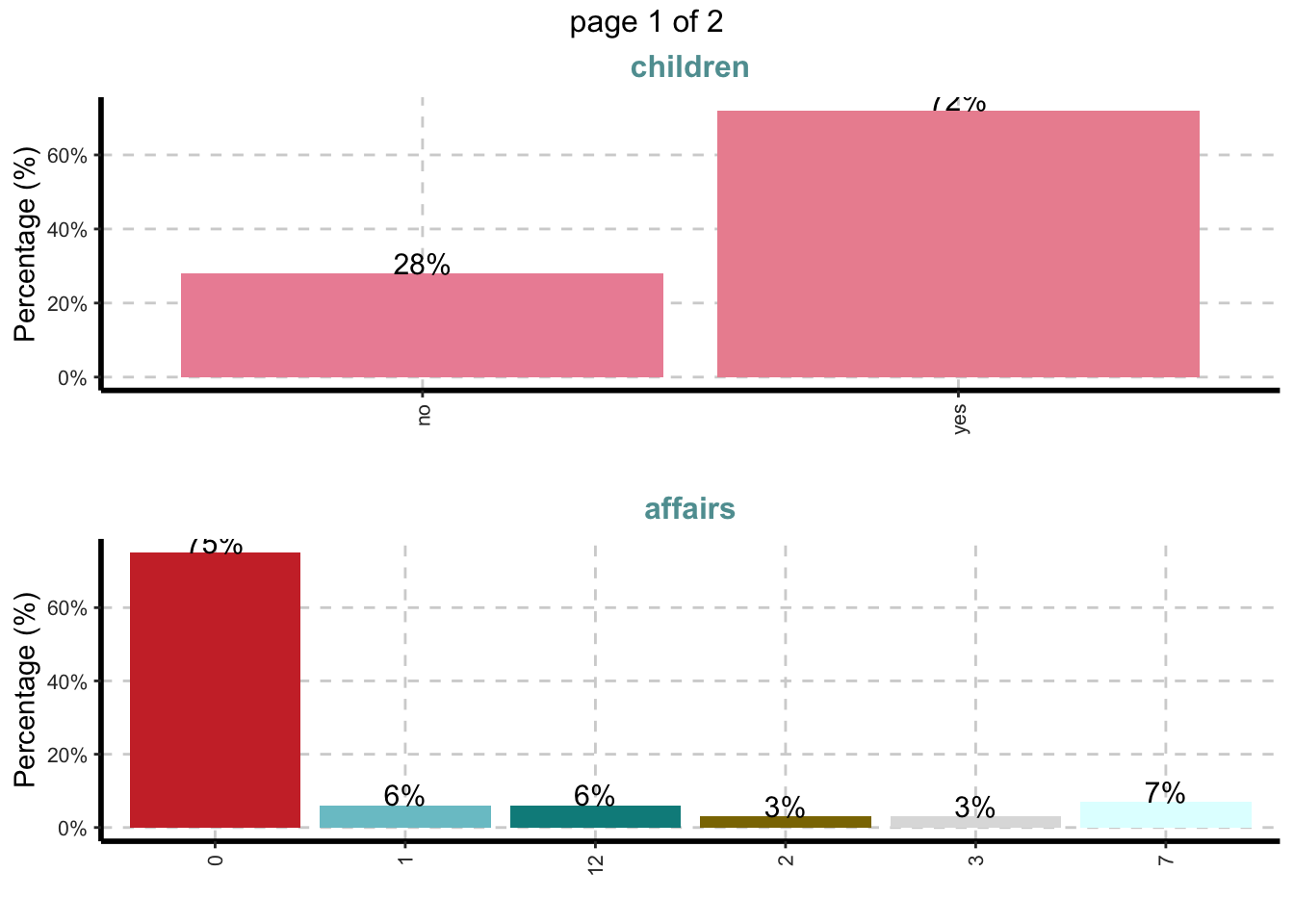

Machine Lerning usando algorítimo não supervisionado de agrupamento
Apenas para efeitos ilustrativos, como estamos supondo que não temos a variável resposta vou remover a coluna affairs do data set e considerarei apenas as variáveis numéricas para fazer uma análise multivariada com o algorítimo de machine learning kmeans.
A função plot_kmeans() pode ser encontrada em meu github no repositório aberto de funções.
Vejamos os resultados:
plot_kmeans(Affairs[,-c(1)] %>% select_if(is.numeric) , 2)
Como podemos observar, foram detectados dois grupos no conjunto de dados. O ideal agora seria fazer uma AED desses clusters identificados e avaliar qual o comportamento dos grupos formados mas como essa variável foi omitida e a seguir discutiremos a avaliação da base diante de da variável resposta, deixo essas análises aos curiosos de plantão.
Mais informações sobre análise multivariava podem ser encontrada no meu post sobre Análise Multivariada com r e também em um kernel que escrevi para a plataforma kaggle.
Além disso disponibilizo uma aplicação Shiny que criei a algum tempo para PCA (Análise de componentes Principais) e tarefa de machine learning com agrupamento nenste link.
Exemplo para o caso 2: A variável de destino é contínua
Agora vamos considerar que estamos diante de um desfecho onde a variável alvo é contínua, para isso será considerada a variável affairs como variável alvo.
Resumo da variável dependente contínua
Descrição da variável affairs:
summary(Affairs[,"affairs"])## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 0.000 0.000 1.456 0.000 12.000Resumo das variáveis numéricas
Estatísticas de resumo quando a variável dependente é contínua Preço.
ExpNumStat(Affairs,
by="A", # Agrupar por A (estatísticas resumidas por Todos), G (estatísticas resumidas por grupo), GA (estatísticas resumidas por grupo e Geral)
Qnt=seq(0,1,0.1), # padrão NULL. Quantis especificados [c (0,25,0,75) encontrarão os percentis 25 e 75]
MesofShape=1, # Medidas de formas (assimetria e curtose)
Outlier=TRUE, # Calcular limite superior , inferior e numero de outliers
round=2) # Arredondamento## Vname Group
## 1 1 All#Se a variável de destino for contínua, as estatísticas de resumo adicionarão a coluna de correlação (Correlação entre a variável de destino e todas as variáveis independentes)Distribuições de variáveis numéricas
Representação gráfica de todas as variáveis numéricas com gráficos de dispersão (bivariada)
Gráfico de dispersão entre todas as variáveis numéricas e a variável de destino affairs. Esta trama ajuda a examinar quão bem uma variável alvo está correlacionada com variáveis dependentes.
Variável dependente é affairs (contínuo).
ExpNumViz(Affairs,
target="affairs", # Variavel alvo
nlim=4, # a variável numérica com valor exclusivo é maior que 4
Page=c(2,2), # formato de saida
sample=NULL) # selecionado aleatoriamente 8 gráficos de dispersão## $`0`

Resumo de variáveis categóricas
Resumo de variáveis categóricas de acordo com a frequência para todas as variáveis independentes categóricas por Affairs
##bin=4, descretized 4 categories based on quantiles
ExpCTable(Affairs, Target="affairs")## VARIABLE CATEGORY affairs:(-0.012,4] affairs:(4,8] affairs:(8,12] TOTAL
## 1 gender female 273 22 20 315
## 2 gender male 248 20 18 286
## 3 gender TOTAL 521 42 38 601
## 4 children no 157 7 7 171
## 5 children yes 364 35 31 430
## 6 children TOTAL 521 42 38 601
## 7 affairs 0 451 0 0 451
## 8 affairs 1 34 0 0 34
## 9 affairs 12 0 0 38 38
## 10 affairs 2 17 0 0 17
## 11 affairs 3 19 0 0 19
## 12 affairs 7 0 42 0 42
## 13 affairs TOTAL 521 42 38 601
## 14 age 17.5 4 0 2 6
## 15 age 22 112 4 1 117
## 16 age 27 138 9 6 153
## 17 age 32 95 11 9 115
## 18 age 37 71 8 9 88
## 19 age 42 44 6 6 56
## 20 age 47 19 1 3 23
## 21 age 52 17 2 2 21
## 22 age 57 21 1 0 22
## 23 age TOTAL 521 42 38 601
## 24 yearsmarried 0.125 11 0 0 11
## 25 yearsmarried 0.417 10 0 0 10
## 26 yearsmarried 0.75 29 0 2 31
## 27 yearsmarried 1.5 85 2 1 88
## 28 yearsmarried 10 57 8 5 70
## 29 yearsmarried 15 165 17 22 204
## 30 yearsmarried 4 94 9 2 105
## 31 yearsmarried 7 70 6 6 82
## 32 yearsmarried TOTAL 521 42 38 601
## 33 religiousness 1 37 5 6 48
## 34 religiousness 2 138 14 12 164
## 35 religiousness 3 105 13 11 129
## 36 religiousness 4 177 6 7 190
## 37 religiousness 5 64 4 2 70
## 38 religiousness TOTAL 521 42 38 601
## 39 education 12 36 2 6 44
## 40 education 14 139 6 9 154
## 41 education 16 108 5 2 115
## 42 education 17 72 9 8 89
## 43 education 18 94 11 7 112
## 44 education 20 67 9 4 80
## 45 education 9 5 0 2 7
## 46 education TOTAL 521 42 38 601
## 47 occupation 1 101 6 6 113
## 48 occupation 2 13 0 0 13
## 49 occupation 3 39 5 3 47
## 50 occupation 4 60 4 4 68
## 51 occupation 5 177 12 15 204
## 52 occupation 6 120 13 10 143
## 53 occupation 7 11 2 0 13
## 54 occupation TOTAL 521 42 38 601
## 55 rating 1 11 1 4 16
## 56 rating 2 43 8 15 66
## 57 rating 3 80 9 4 93
## 58 rating 4 169 18 7 194
## 59 rating 5 218 6 8 232
## 60 rating TOTAL 521 42 38 601Distribuições de variáveis categóricas
Essa função varre automaticamente cada variável e cria um gráfico de barras para variáveis categóricas.
Gráficos de barra para todas as variáveis categóricas
ExpCatViz(Affairs,
target="affairs", # Variavel target
fname=NULL, # Nome do arquivo de saida, default é pdf
clim=10,# categorias máximas a incluir nos gráficos de barras.
margin=2,# índice, 1 para proporções baseadas em linha e 2 para proporções baseadas em colunas
Page = c(2,1), # padrao de saida
sample=4) # seleção aleatória de plot## $`0`
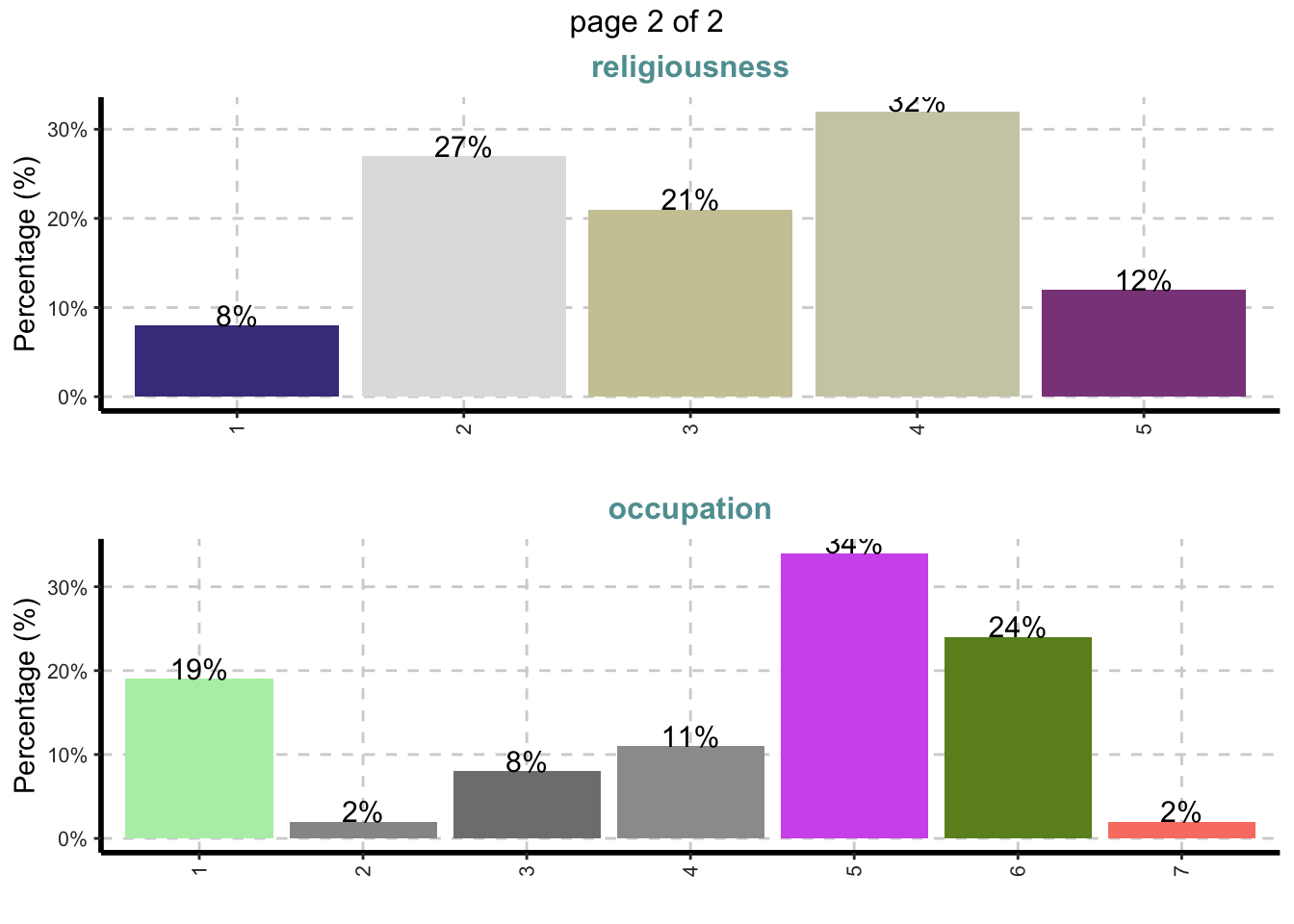
Avaliando a correlação entre as variáveis
library(ggplot2)
library(dplyr)
library(GGally)
data("Affairs")
#Correlaçoes cruzadas
Affairs%>%
select(age:rating,affairs)%>%
ggpairs(lower = list(continuous = my_fn,combo=wrap("facethist", binwidth=1),
continuous=wrap(my_bin, binwidth=0.25)),aes(fill=affairs))+theme_bw()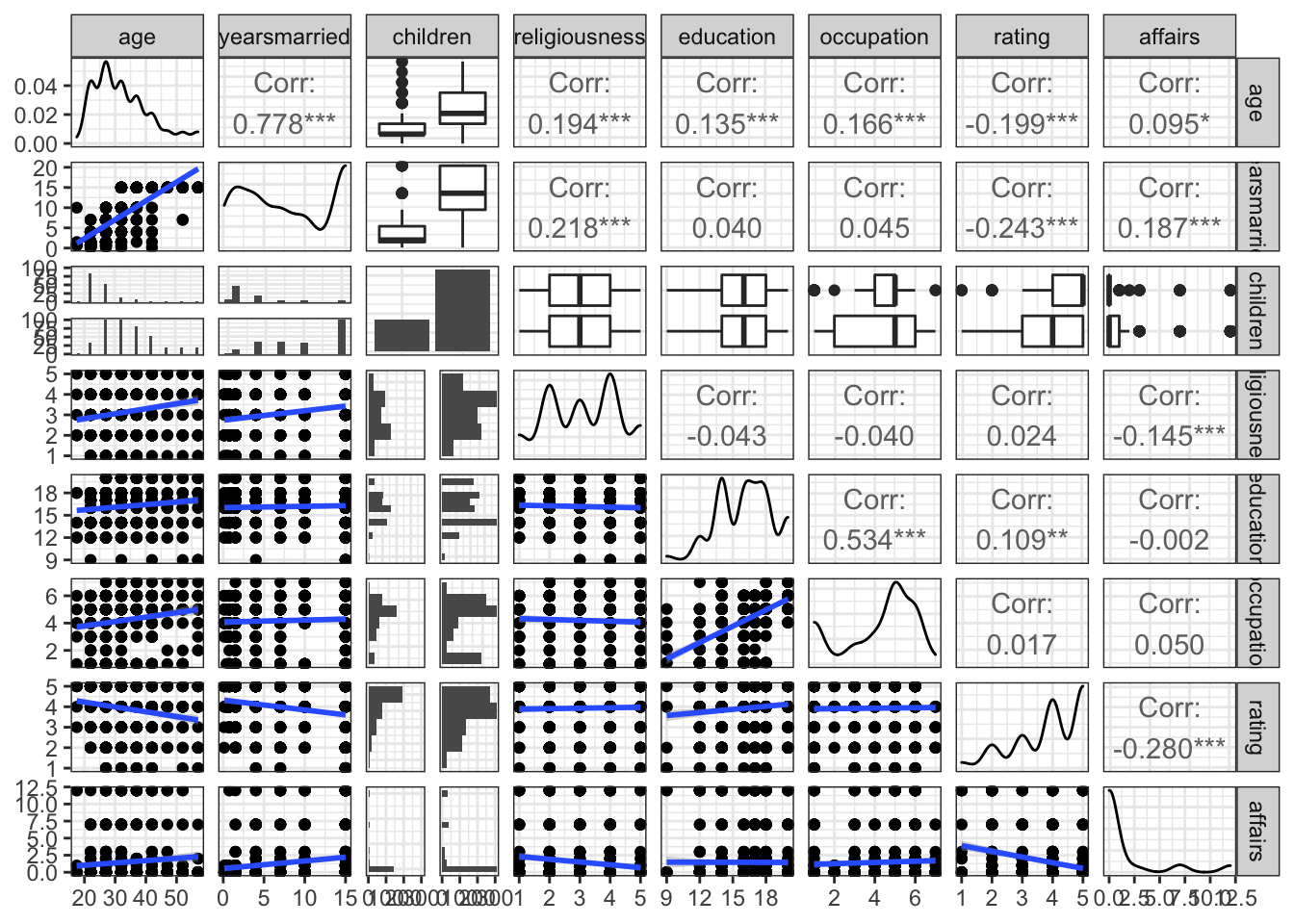
ggcorr(Affairs,label = T,nbreaks = 5,label_round = 4)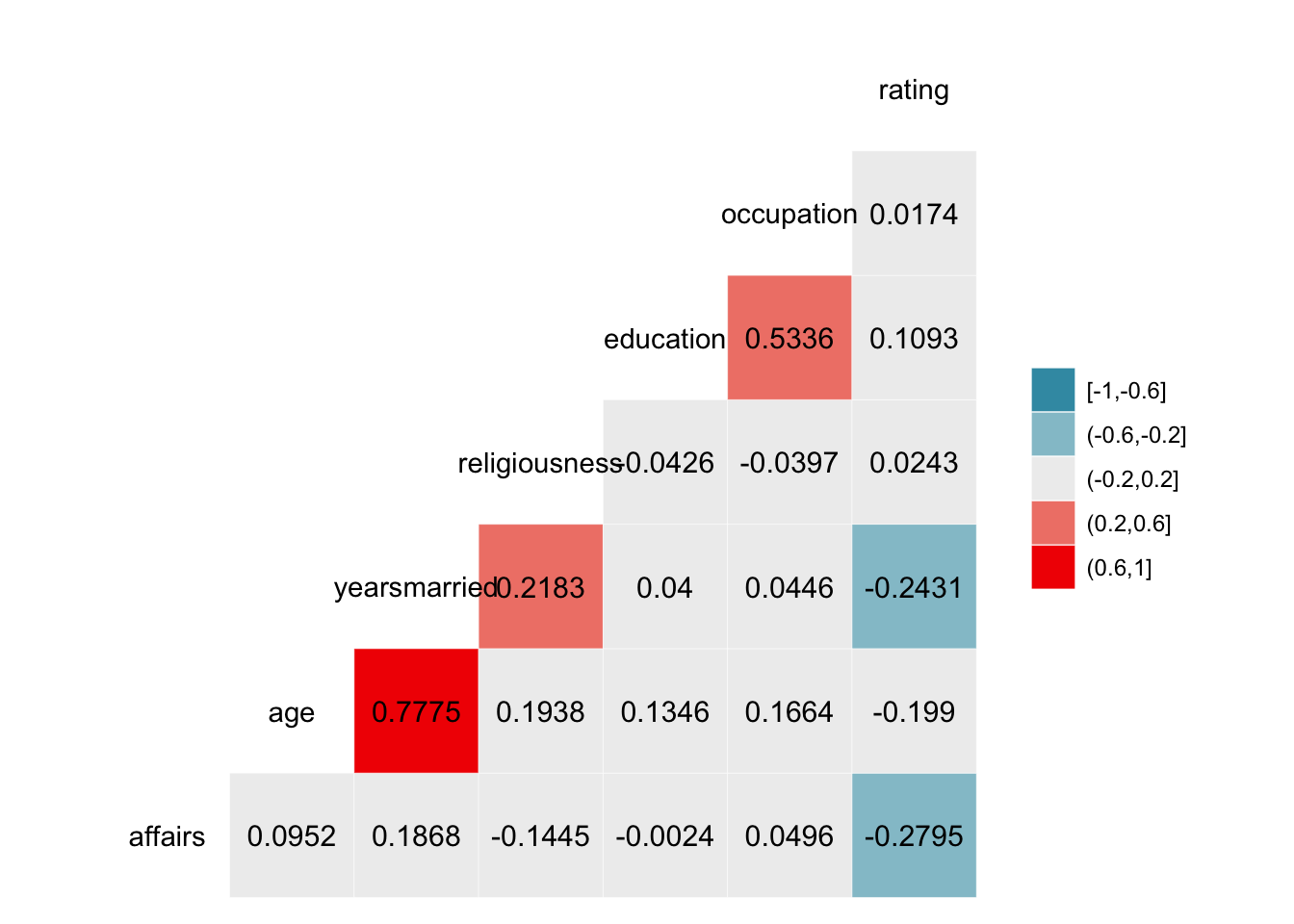
Modelo de regressão linear usando stepwiseAIC
Por fim, vamos ajustar um modelo de regressão linear para entender quais são as variáveis significativas para explicar a variação da variável resposta e qual o efeito de cada uma dessas variáveis explicativas no nosso desfecho.
Com o R base é possível ajustar um modelo de regressão linear simples utilizando a função lm() e em seguida usar a função step() para utilizar técnicas como stepwise, porém como quero utilizar também a técnica de validação cruzada. Para isso vou utilizar o pacote caret, muito famoso por facilitar o ajuste de modelos de machine learning (ou mesmo modelos estatísticos tradicionais).
Além disso estou usando as transformações center(), que subtrai a média dos dados e scale() divide pelo desvio padrão.
data("Affairs")
library(caret)
set.seed(123)
index <- sample(1:2,nrow(Affairs),replace=T,prob=c(0.8,0.2))
train = Affairs[index==1,] %>%as.data.frame()
test = Affairs[index==2,] %>%as.data.frame()
# Setando os parâmetros para o controle do ajuste do modelo:
fitControl <- trainControl(method = "repeatedcv", # 10fold cross validation
number = 10, repeats=5 # do 5 repititições of cv
)
# Regressão Linear com Stepwise
set.seed(825)
lmFit <- train(affairs ~ ., data = train,
method = "lmStepAIC",
trControl = fitControl,
preProc = c("center", "scale"),trace=F)
summary(lmFit)##
## Call:
## lm(formula = .outcome ~ age + yearsmarried + religiousness +
## occupation + rating, data = dat)
##
## Residuals:
## Min 1Q Median 3Q Max
## -5.1452 -1.7819 -0.7601 0.2719 11.3518
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.4146 0.1401 10.096 < 2e-16 ***
## age -0.6890 0.2291 -3.007 0.002779 **
## yearsmarried 1.1058 0.2302 4.804 2.09e-06 ***
## religiousness -0.5121 0.1455 -3.519 0.000475 ***
## occupation 0.3858 0.1445 2.669 0.007858 **
## rating -0.7830 0.1470 -5.326 1.55e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.07 on 474 degrees of freedom
## Multiple R-squared: 0.144, Adjusted R-squared: 0.135
## F-statistic: 15.95 on 5 and 474 DF, p-value: 1.542e-14Como podemos ver as variáveis Idade, Anos de casado, religiosidade, ocupação e como avaliam o próprio relacionamento se apresentaram significantes
Como o \(R^2=0,144\), conclui-se que \(14,4%\) da variação da quantidade de vezes que foi envolvida em caso extraconjugal no último ano é explicada pelo modelo ajustado.
Observando a coluna das estimativas, podemos notar o quanto varia a quantidade de vezes que foi envolvido em caso extraconjugal ao aumentar em 1 unidade cada uma das variáveis explicativas.
Além disso o valor p obtido através da estatística F foi menor do que \(\alpha = 0.05\), o que implica que pelo menos uma das variáveis explicativas tem relação significativa com a variável resposta.
Selecionando apenas as variáveis selecionadas com o ajuste do modelo:
train=as.data.frame(train[,c(1,3,4,6,8,9)])
test=as.data.frame(test[,c(1,3,4,6,8,9)])Diagnóstico do modelo
Existem varias formas e técnicas de se avaliar o ajuste de um modelo e como o foco deste post é apresentar as utilidades do pacote SmartEAD irei fazer uma avaliação muito breve sobre os resíduos, apresento mais algumas maneiras no post sobre pacotes do R para avaliar o ajuste de modelos.
Avaliando residuos
library(GGally)
# calculate all residuals prior to display
residuals <- lapply(train[2:ncol(train)], function(x) {
summary(lm(affairs ~ x, data = train))$residuals
})
# add a 'fake' column
train$Residual <- seq_len(nrow(train))
# calculate a consistent y range for all residuals
y_range <- range(unlist(residuals))
# plot the data
ggduo(
train,
2:6, c(1,7),
types = list(continuous = lm_or_resid)
)+ theme_bw()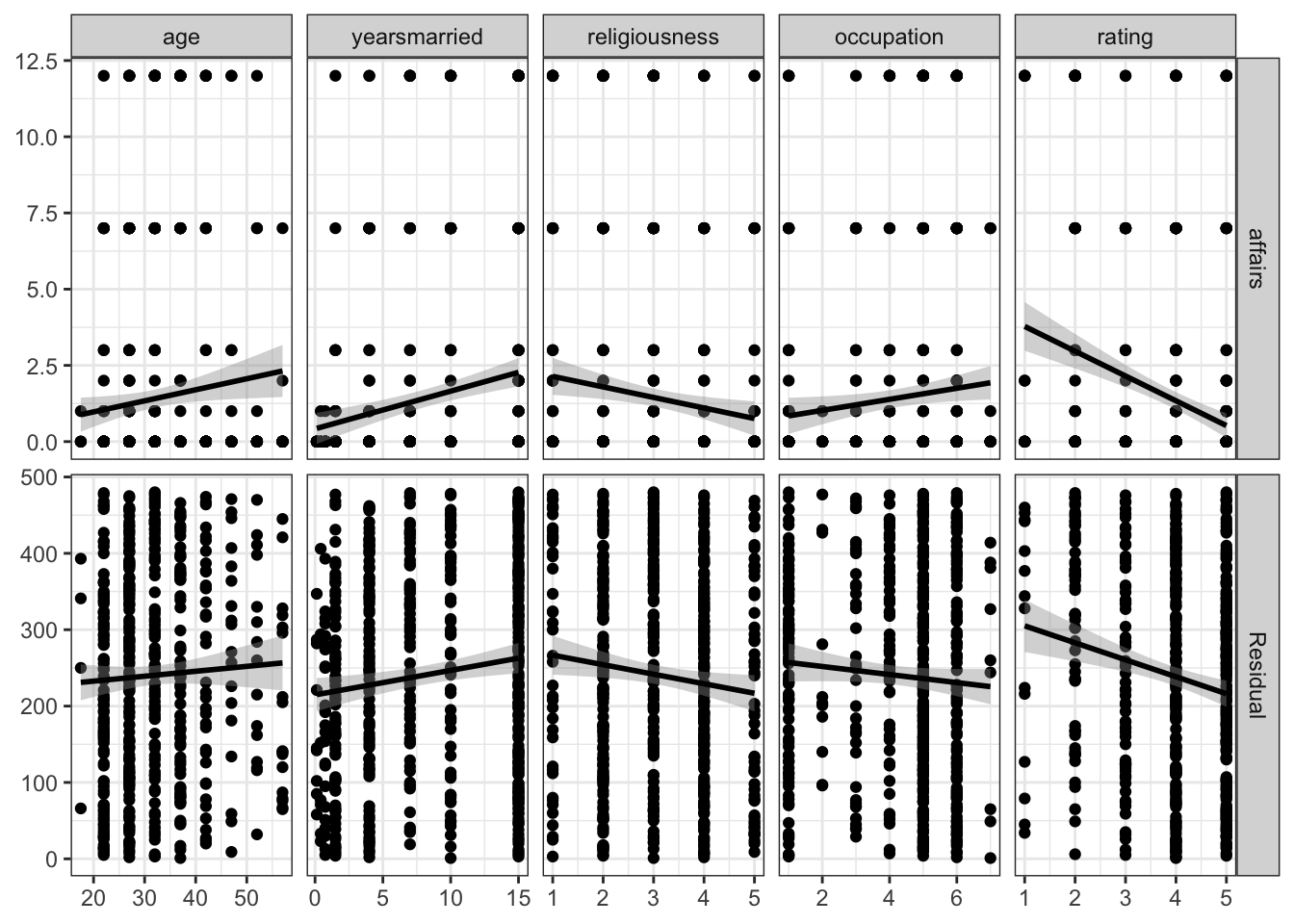
train=train%>%
select(-Residual)Neste gráfico é possível observar como se comportam os ajustes de modelos lineares de cada variável explicativa em relação à variável resposta e além disso na segunda linha é possível notar o comportamento dos resíduos no modelo.
Uma das suposições do ajuste de um modelo linear normal é de que \(\epsilon \sim N(0,\sigma^2)\) e visualmente parece que essa condição não deve ser atendida, pois esperaríamos algo como uma “nuvem” aleatória de pontos em torno de zero.
Residuos e medidas de influencia
Além da suposição da normalidade dos resíduos, existem ainda mais detalhes do comportamento desses erros, uma breve apresentação no gráfico a seguir:
library(ggfortify)
autoplot(lmFit$finalModel, which = 1:6, data = train,
colour = 'affairs', label.size = 3,
ncol = 3)+theme_classic()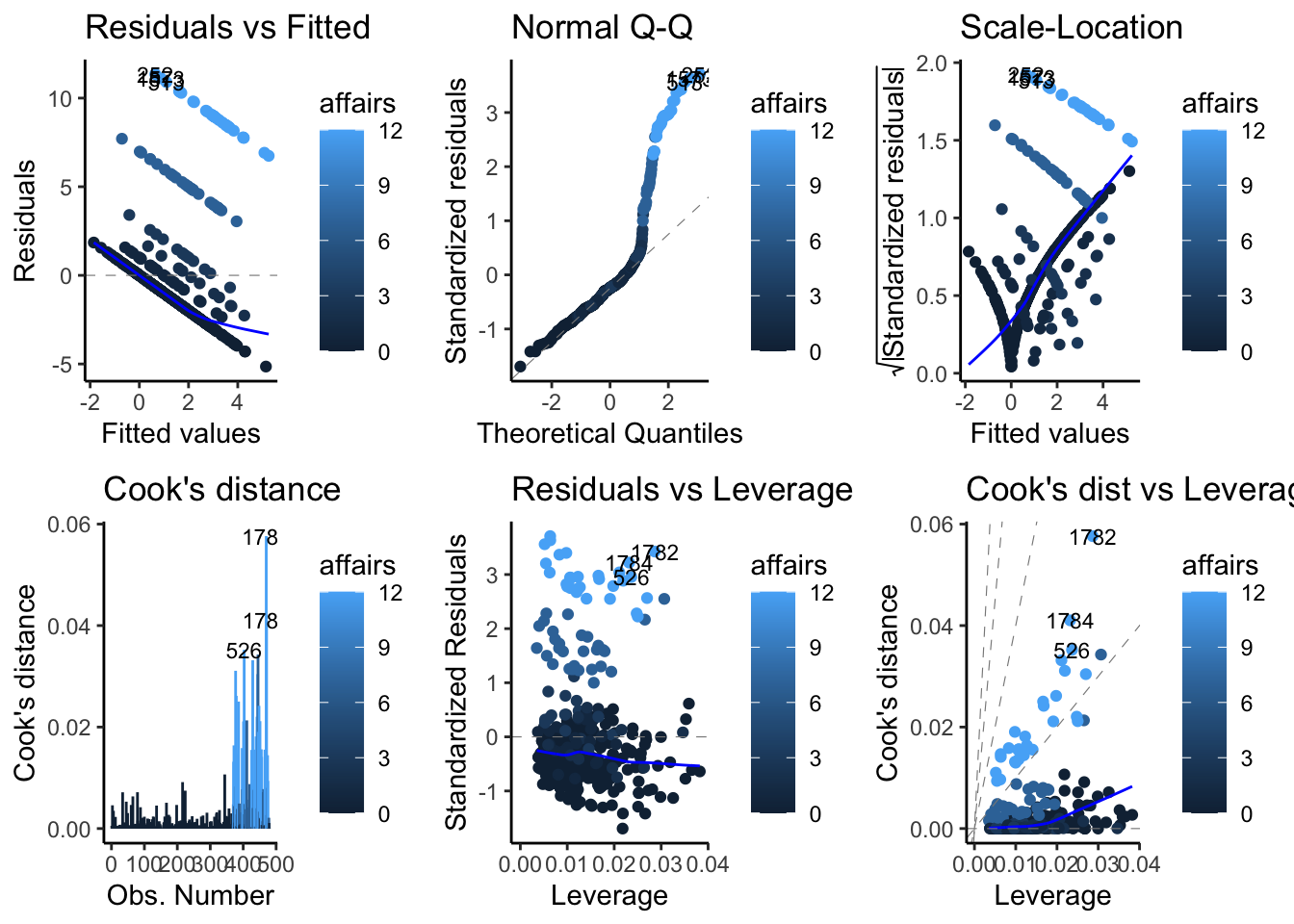
Pelo que parece no gráfico com título “Normal Q-Q”, as variáveis associadas à variável resposta com valores acima de 6 se comportam de forma inesperadas quando comparadas com os quantis teóricos.
Exemplo para o caso 3: a variável de destino é categórica
Para finalizar a avaliação da base de dados, a Variável alvo será discretizado de tal forma:
\[ 1 = \text{se affairs} > 0\\ 0 = c.c. \]
Essa transformação será utilizada apenas com fins ilustrativos do algorítimo de árvore de decisões, que está ficando muito comum na ciência de dados como uma tarefa supervisionada de machine learning.
Affairs = Affairs %>%
mutate(daffairs = ifelse(Affairs$affairs!=0,1,0)) %>%
mutate(daffairs = as.factor(daffairs))%>%
select(-affairs)
levels(Affairs$daffairs) = c("Não", "Sim")Resumo das variáveis numéricas
Resumo de todas as variáveis numéricas
ExpNumStat(Affairs,
by="A", # Agrupar por A (estatísticas resumidas por Todos), G (estatísticas resumidas por grupo), GA (estatísticas resumidas por grupo e Geral)
gp="daffairs", # Variavel alvo
Qnt=seq(0,1,0.1), # padrão NULL. Quantis especificados [c (0,25,0,75) encontrarão os percentis 25 e 75]
MesofShape=1, # Medidas de formas (assimetria e curtose)
Outlier=TRUE, # Calcular limite superior , inferior e numero de outliers
round=2) # Arredondamento## Vname Group
## 1 1 AllDistribuições de variáveis numéricas
Box plots para todas as variáveis numéricas vs variável dependente categórica - Comparação bivariada apenas com categorias
Boxplot para todos os atributos numéricos por cada categoria de affair
ExpNumViz(Affairs, target="daffairs") # amostra de variaveis para o resumo## [[1]]
##
## [[2]]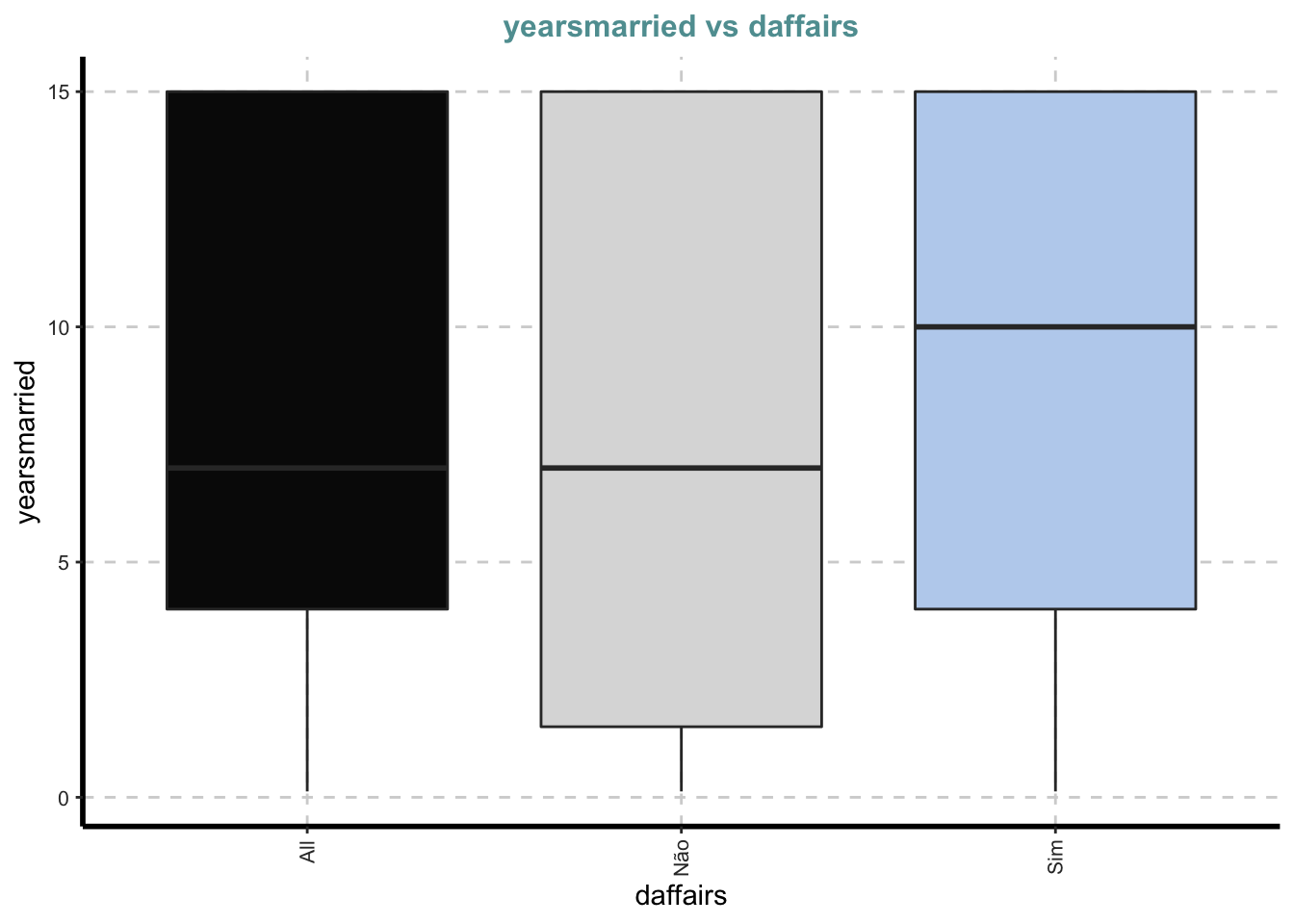
##
## [[3]]
##
## [[4]]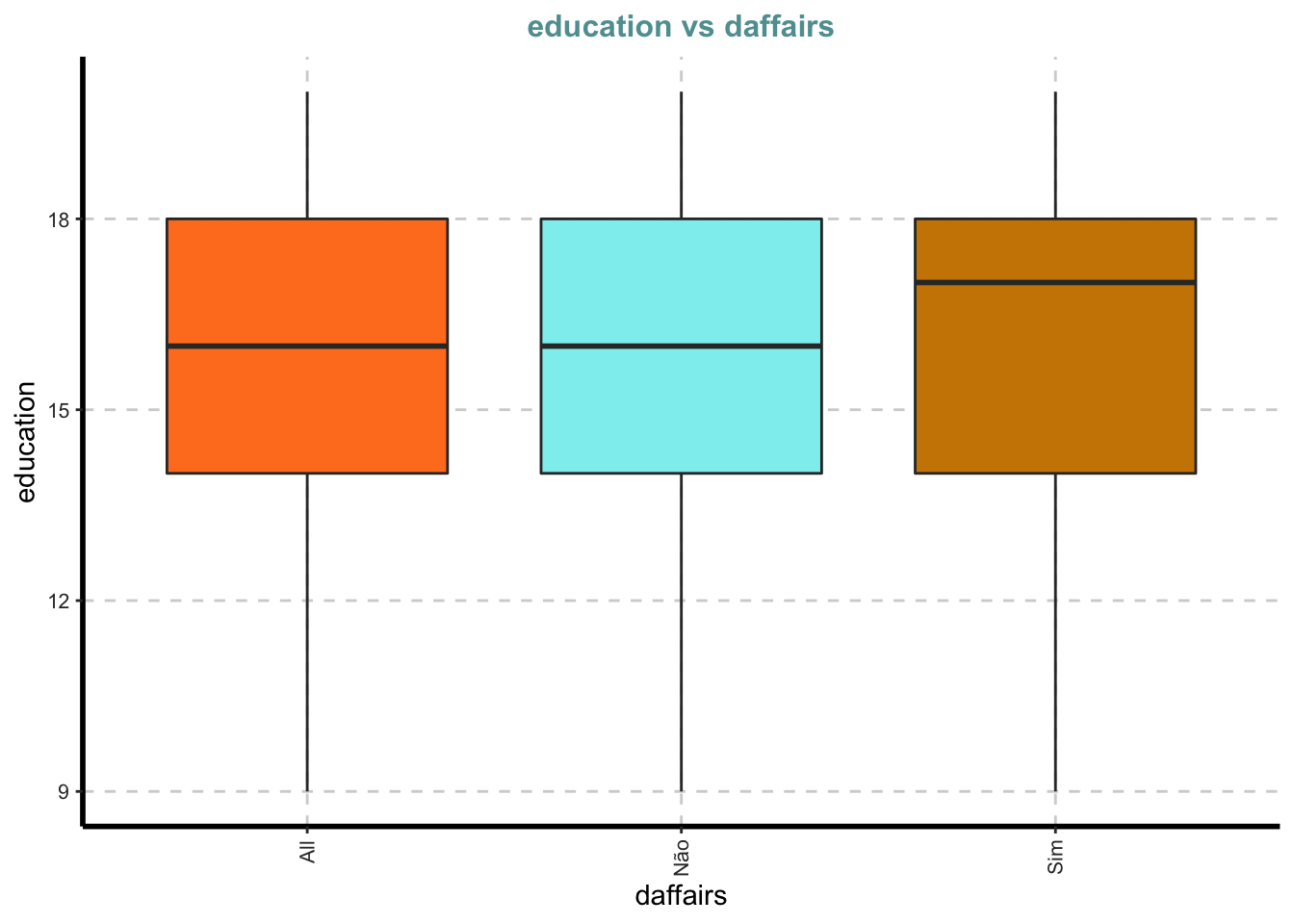
##
## [[5]]
##
## [[6]]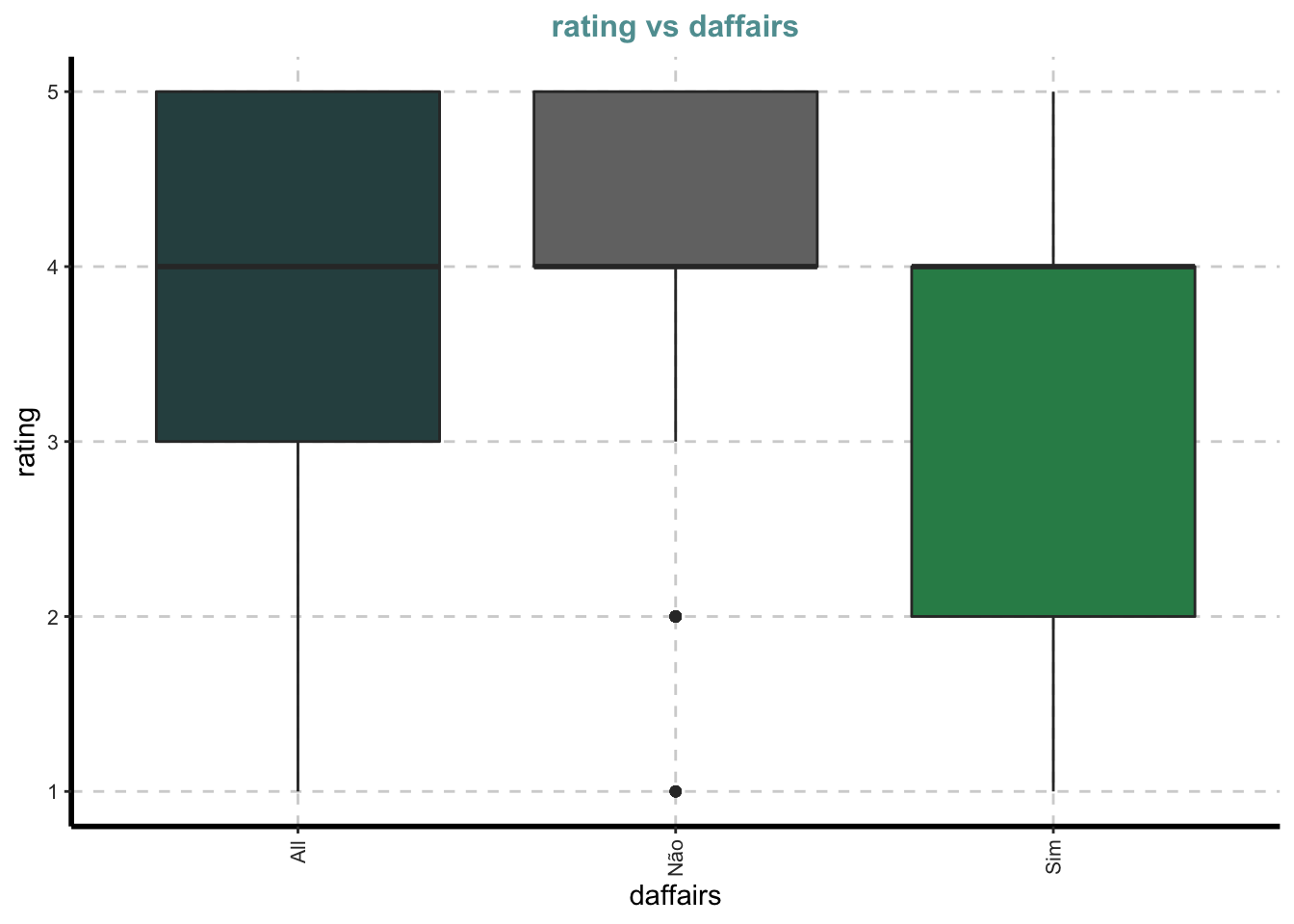
Resumo das variáveis categóricas
Tabulação cruzada com variável de destino com tabelas customizadas entre todas as variáveis independentes categóricas e a variável de destino daffairs:
ExpCTable(Affairs,
Target="daffairs", # variavel alvo
margin=1, # 1 para proporcoes por linha, 2 para colunas
clim=10, # maximo de categorias consideradas por frequencia/ custom table
round=2, # arredondar
per=F) # valores percentuais. Tabela padrão dará contagens.## VARIABLE CATEGORY daffairs:Não daffairs:Sim TOTAL
## 1 gender female 243 72 315
## 2 gender male 208 78 286
## 3 gender TOTAL 451 150 601
## 4 children no 144 27 171
## 5 children yes 307 123 430
## 6 children TOTAL 451 150 601
## 7 age 17.5 3 3 6
## 8 age 22 101 16 117
## 9 age 27 117 36 153
## 10 age 32 77 38 115
## 11 age 37 65 23 88
## 12 age 42 38 18 56
## 13 age 47 16 7 23
## 14 age 52 15 6 21
## 15 age 57 19 3 22
## 16 age TOTAL 451 150 601
## 17 yearsmarried 0.125 10 1 11
## 18 yearsmarried 0.417 9 1 10
## 19 yearsmarried 0.75 28 3 31
## 20 yearsmarried 1.5 76 12 88
## 21 yearsmarried 10 49 21 70
## 22 yearsmarried 15 142 62 204
## 23 yearsmarried 4 78 27 105
## 24 yearsmarried 7 59 23 82
## 25 yearsmarried TOTAL 451 150 601
## 26 religiousness 1 28 20 48
## 27 religiousness 2 123 41 164
## 28 religiousness 3 86 43 129
## 29 religiousness 4 157 33 190
## 30 religiousness 5 57 13 70
## 31 religiousness TOTAL 451 150 601
## 32 education 12 31 13 44
## 33 education 14 119 35 154
## 34 education 16 95 20 115
## 35 education 17 62 27 89
## 36 education 18 79 33 112
## 37 education 20 60 20 80
## 38 education 9 5 2 7
## 39 education TOTAL 451 150 601
## 40 occupation 1 90 23 113
## 41 occupation 2 10 3 13
## 42 occupation 3 32 15 47
## 43 occupation 4 47 21 68
## 44 occupation 5 160 44 204
## 45 occupation 6 104 39 143
## 46 occupation 7 8 5 13
## 47 occupation TOTAL 451 150 601
## 48 rating 1 8 8 16
## 49 rating 2 33 33 66
## 50 rating 3 66 27 93
## 51 rating 4 146 48 194
## 52 rating 5 198 34 232
## 53 rating TOTAL 451 150 601Distribuições de variáveis categóricas
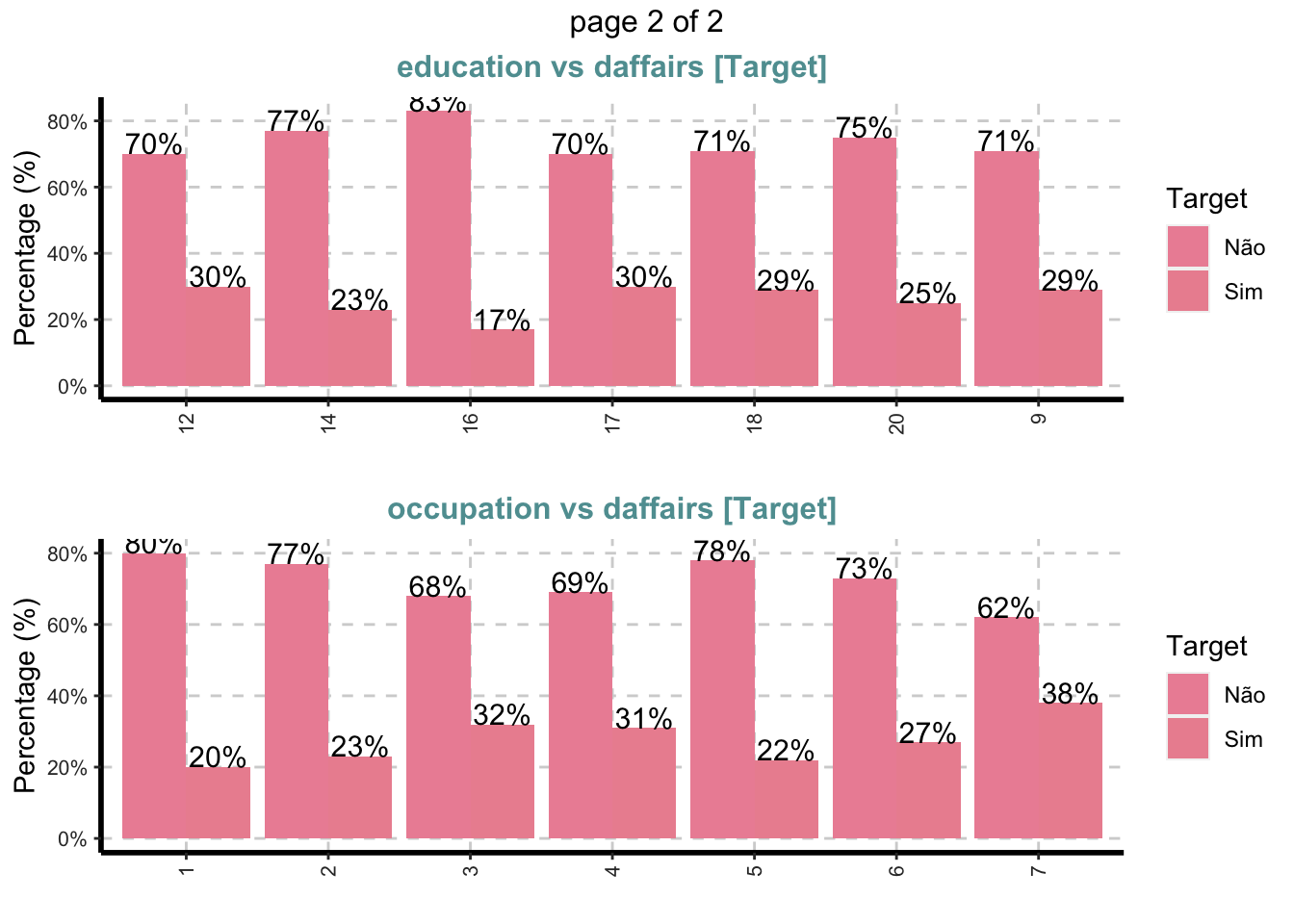
Gráfico de barras empilhadas com barras verticais ou horizontais para todas as variáveis categóricas
ExpCatViz(Affairs,
target="daffairs",
fname=NULL, # Nome do arquivo de saida, default é pdf
clim=10,# categorias máximas a incluir nos gráficos de barras.
margin=2,# índice, 1 para proporções baseadas em linha e 2 para proporções baseadas em colunas
Page = c(2,1), # padrao de saida
sample=4) # seleção aleatória de plot## $`0`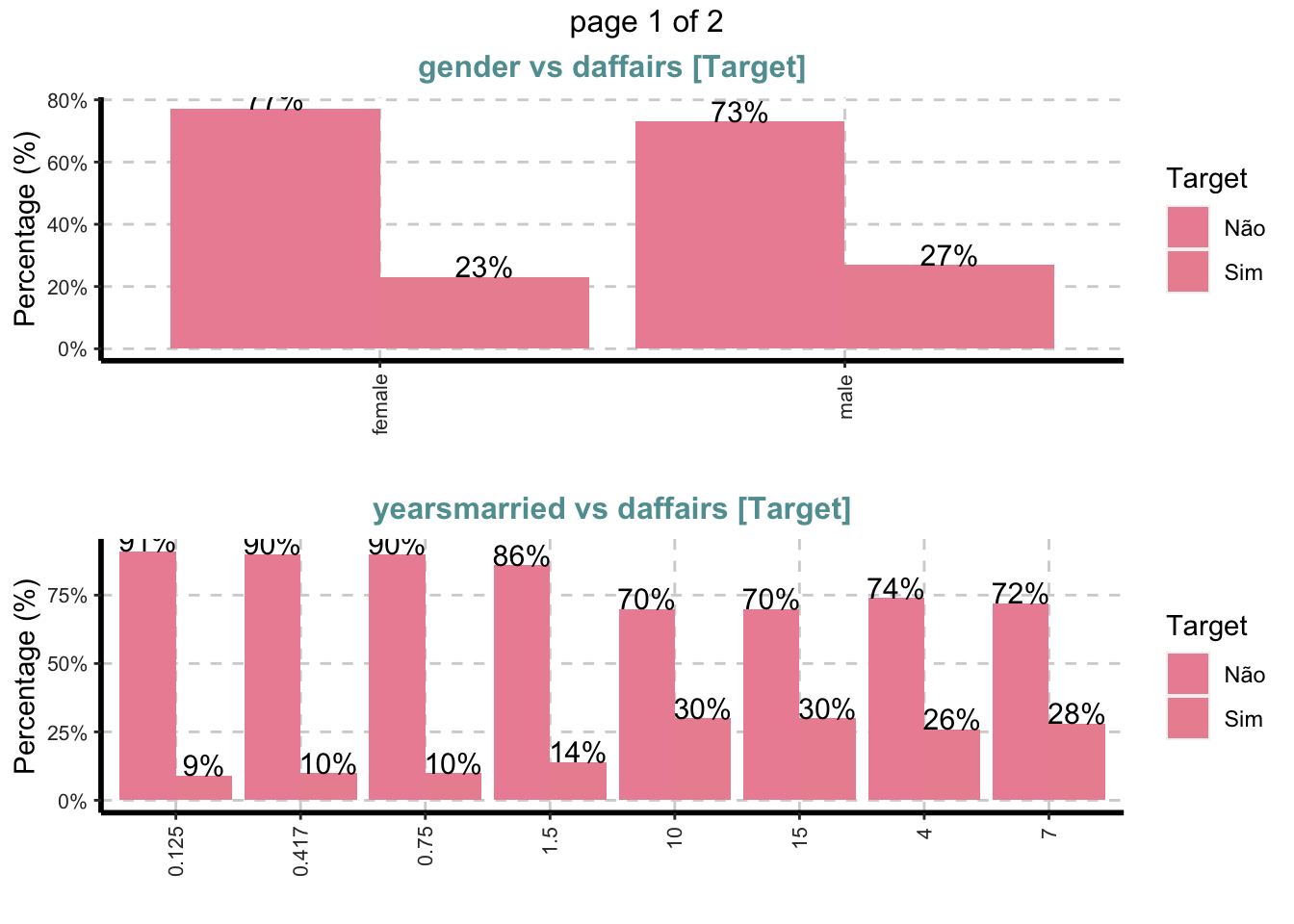
Valor da informação
IV é o peso da evidência e valores da informação, \(ln(odss) \times(pct0 - pct1)\) onde \(pct1 =\frac{\text{"boas observações"}}{\text{"total boas observações"}}\); \(pct0 = \frac{"\text{observações ruins"} }{ \text{"total de observações ruins"}}\) e $odds = $
ExpCatStat(Affairs %>% mutate(daffairs = if_else(daffairs=="Não", 0, 1)) ,
Target="daffairs",
result = "IV") %>%
select(-one_of("Target","Ref_1","Ref_0"))## Variable Class Out_1 Out_0 TOTAL Per_1 Per_0 Odds WOE IV
## 1 gender.1 female 72 243 315 0.48 0.54 0.79 -0.12 0.01
## 2 gender.2 male 78 208 286 0.52 0.46 1.27 0.12 0.01
## 3 children.1 no 27 144 171 0.18 0.32 0.47 -0.58 0.08
## 4 children.2 yes 123 307 430 0.82 0.68 2.14 0.19 0.03
## 5 age.1 17.5 3 3 6 0.02 0.01 3.05 0.69 0.01
## 6 age.2 22 16 101 117 0.11 0.22 0.41 -0.69 0.08
## 7 age.3 27 36 117 153 0.24 0.26 0.90 -0.08 0.00
## 8 age.4 32 38 77 115 0.25 0.17 1.65 0.39 0.03
## 9 age.5 37 23 65 88 0.15 0.14 1.08 0.07 0.00
## 10 age.6 42 18 38 56 0.12 0.08 1.48 0.41 0.02
## 11 age.7 47 7 16 23 0.05 0.04 1.33 0.22 0.00
## 12 age.8 52 6 15 21 0.04 0.03 1.21 0.29 0.00
## 13 age.9 57 3 19 22 0.02 0.04 0.46 -0.69 0.01
## 14 yearsmarried.1 0.125 1 10 11 0.01 0.02 0.30 -0.69 0.01
## 15 yearsmarried.2 0.417 1 9 10 0.01 0.02 0.33 -0.69 0.01
## 16 yearsmarried.3 0.75 3 28 31 0.02 0.06 0.31 -1.11 0.04
## 17 yearsmarried.4 1.5 12 76 88 0.08 0.17 0.43 -0.76 0.07
## 18 yearsmarried.5 10 21 49 70 0.14 0.11 1.34 0.24 0.01
## 19 yearsmarried.6 15 62 142 204 0.41 0.31 1.53 0.28 0.03
## 20 yearsmarried.7 4 27 78 105 0.18 0.17 1.05 0.06 0.00
## 21 yearsmarried.8 7 23 59 82 0.15 0.13 1.20 0.14 0.00
## 22 religiousness.1 1 20 28 48 0.13 0.06 2.32 0.77 0.05
## 23 religiousness.2 2 41 123 164 0.27 0.27 1.00 0.00 0.00
## 24 religiousness.3 3 43 86 129 0.29 0.19 1.71 0.43 0.04
## 25 religiousness.4 4 33 157 190 0.22 0.35 0.53 -0.46 0.06
## 26 religiousness.5 5 13 57 70 0.09 0.13 0.66 -0.37 0.01
## 27 education.1 12 13 31 44 0.09 0.07 1.29 0.25 0.00
## 28 education.2 14 35 119 154 0.23 0.26 0.85 -0.13 0.00
## 29 education.3 16 20 95 115 0.13 0.21 0.58 -0.48 0.04
## 30 education.4 17 27 62 89 0.18 0.14 1.38 0.25 0.01
## 31 education.5 18 33 79 112 0.22 0.18 1.33 0.20 0.01
## 32 education.6 20 20 60 80 0.13 0.13 1.00 0.00 0.00
## 33 education.7 9 2 5 7 0.01 0.01 1.21 0.00 0.00
## 34 occupation.1 1 23 90 113 0.15 0.20 0.73 -0.29 0.01
## 35 occupation.2 2 3 10 13 0.02 0.02 0.90 0.00 0.00
## 36 occupation.3 3 15 32 47 0.10 0.07 1.45 0.36 0.01
## 37 occupation.4 4 21 47 68 0.14 0.10 1.40 0.34 0.01
## 38 occupation.5 5 44 160 204 0.29 0.35 0.75 -0.19 0.01
## 39 occupation.6 6 39 104 143 0.26 0.23 1.17 0.12 0.00
## 40 occupation.7 7 5 8 13 0.03 0.02 1.91 0.41 0.00
## 41 rating.1 1 8 8 16 0.05 0.02 3.12 0.92 0.03
## 42 rating.2 2 33 33 66 0.22 0.07 3.57 1.14 0.17
## 43 rating.3 3 27 66 93 0.18 0.15 1.28 0.18 0.01
## 44 rating.4 4 48 146 194 0.32 0.32 0.98 0.00 0.00
## 45 rating.5 5 34 198 232 0.23 0.44 0.37 -0.65 0.14Testes estatísticos
Além de toda a informação visual e das estatísticas descritivas, ainda contamos com alguma função que fornece estatísticas resumidas para todas as colunas de caracteres ou categóricas no data frame
ExpCatStat(Affairs %>% mutate(daffairs = if_else(daffairs=="Não", 0, 1)),
Target="daffairs", # variavel alvo
result = "Stat") # resumo de estatisticas## Variable Target Unique Chi-squared p-value df IV Value Cramers V
## 1 gender daffairs 2 1.334 0.248 1 0.02 0.05
## 2 children daffairs 2 10.055 0.002 1 0.11 0.13
## 3 age daffairs 9 17.771 0.023 8 0.15 0.17
## 4 yearsmarried daffairs 8 17.177 0.016 7 0.17 0.17
## 5 religiousness daffairs 5 19.354 0.001 4 0.16 0.18
## 6 education daffairs 7 7.057 0.316 6 0.06 0.11
## 7 occupation daffairs 7 6.718 0.348 6 0.04 0.11
## 8 rating daffairs 5 41.433 0.000 4 0.35 0.26
## Degree of Association Predictive Power
## 1 Very Weak Not Predictive
## 2 Weak Somewhat Predictive
## 3 Weak Somewhat Predictive
## 4 Weak Somewhat Predictive
## 5 Weak Somewhat Predictive
## 6 Weak Not Predictive
## 7 Weak Not Predictive
## 8 Moderate Highly PredictiveOs critérios usados para classificação de poder preditivo variável categórico são
Se o valor da informação for <0,03, então, poder de previsão = “Não Preditivo”
Se o valor da informação é de 0,3 a 0,1, então o poder preditivo = “um pouco preditivo”
Se o valor da informação for de 0,1 a 0,3, então, poder preditivo = “Medium Predictive”
Se o valor da informação for> 0.3, então, poder preditivo = “Altamente Preditivo”
Nota para a variável rating que segundo essas regras, demonstrou alto poder preditivo.
Machine Learning com Random Forest
O algorítimo supervisionado de machine learning conhecido como Random Forest é uma grande caixa preta. Apresenta resultados muito robustos pois combina o resultado de várias árvores de decisões e pode ser facilmente aplicada com o pacote caret.
No livro do pacote caret o algorítimo é apresentado da seguinte maneira: “segundo o pacote do R: Para cada árvore, a precisão da previsão na parte fora do saco dos dados é registrada. Então, o mesmo é feito após a permutação de cada variável preditora. A diferença entre as duas precisões é calculada pela média de todas as árvores e normalizada pelo erro padrão. Para a regressão, o MSE é calculado nos dados fora da bolsa para cada árvore e, em seguida, o mesmo é computado após a permutação de uma variável. As diferenças são calculadas e normalizadas pelo erro padrão. Se o erro padrão é igual a 0 para uma variável, a divisão não é feita.”
Não entrarei em muitos detalhes sobre o algorítimo pois esta parte é apenas um demonstrativo dos diferentes cenários de análise exploratória dos dados. Serão comentadas apenas algumas métricas utilizadas.
Ajuste com o algorítimo Random Forest:
library(caret)
set.seed(1)
index <- sample(1:2,nrow(Affairs),replace=T,prob=c(0.8,0.2))
train = Affairs[index==1,] %>%as.data.frame()
test = Affairs[index==2,] %>%as.data.frame()
# Setando os parâmetros para o controle do ajuste do modelo:
fitControl <- trainControl(method = "repeatedcv", # 10fold cross validation
number = 10
)
# Random Forest
set.seed(825)
antes = Sys.time()
rfFit <- train(daffairs ~ ., data = train,
method = "rf",
trControl = fitControl,
trace=F,
preProc = c("center", "scale"))
antes - Sys.time() # Para saber quanto tempo durou o ajuste## Time difference of -13.38876 secsResultados do ajuste:
rfFit## Random Forest
##
## 484 samples
## 8 predictor
## 2 classes: 'Não', 'Sim'
##
## Pre-processing: centered (8), scaled (8)
## Resampling: Cross-Validated (10 fold, repeated 1 times)
## Summary of sample sizes: 436, 436, 435, 435, 435, 436, ...
## Resampling results across tuning parameters:
##
## mtry Accuracy Kappa
## 2 0.7539966 0.1369868
## 5 0.7292942 0.1727691
## 8 0.7231718 0.1613695
##
## Accuracy was used to select the optimal model using the largest value.
## The final value used for the model was mtry = 2.Accurary e Kappa
Essas são as métricas padrão usadas para avaliar algoritmos em conjuntos de dados de classificação binária.
- Accuray: é a porcentagem de classificar corretamente as instâncias fora de todas as instâncias. É mais útil em uma classificação binária do que problemas de classificação de várias classes, porque pode ser menos claro exatamente como a precisão é dividida entre essas classes (por exemplo, você precisa ir mais fundo com uma matriz de confusão).
- Kappa ou Kappa de Cohen é como a precisão da classificação, exceto que é normalizado na linha de base da chance aleatória em seu conjunto de dados. É uma medida mais útil para usar em problemas que têm um desequilíbrio nas classes (por exemplo, divisão de 70 a 30 para as classes 0 e 1 e você pode atingir 70% de precisão prevendo que todas as instâncias são para a classe 0).
A seguir a “Variable Importance” de cada variável:
rfImp = varImp(rfFit);rfImp## rf variable importance
##
## Overall
## rating 100.00
## age 94.66
## religiousness 85.77
## education 78.99
## yearsmarried 67.41
## occupation 62.48
## gendermale 6.94
## childrenyes 0.00plot(rfImp)
A função dimensiona automaticamente as pontuações de importância entre 0 e 100, os escores de importância da variável em Random Forest são medidas agregadas. Eles apenas quantificam o impacto do preditor, não o efeito específico, para isso utilizamos o ajuste um modelo paramétrico onde conseguimos estimar termos estruturais.
É claro que existem muitos adentos a serem feitos tanto na forma como os dados foram apresentados no ajuste do modelo linear e no Random Forest, mas como a finalidade do post continua sendo apresentar o pacote SmartEAD, encerrarei a avaliação por aqui.
Caso alguém queira entender com mais detalhes a avaliação de modelos de machine learning, talvez o livro do pacote caret seja uma alternativa interessante para ter uma noção geral.
Todos os modelos estão errados, alguns são úteis - George Box
Não conseguimos nenhum modelo útil que quantificasse as incertezas nas modelagens deste post mas conseguimos executar praticamente todas as funções do pacote SmartEAD e foi muito útil para conhecer a base em poucas linhas, obrigado Dayanand Ubrangala, Kiran R. e Ravi Prasad Kondapalli!






























Share this post
Twitter
LinkedIn
Email